0.003 Is 1/10 Of What Decimal
Breaking News Today
Jun 07, 2025 · 5 min read
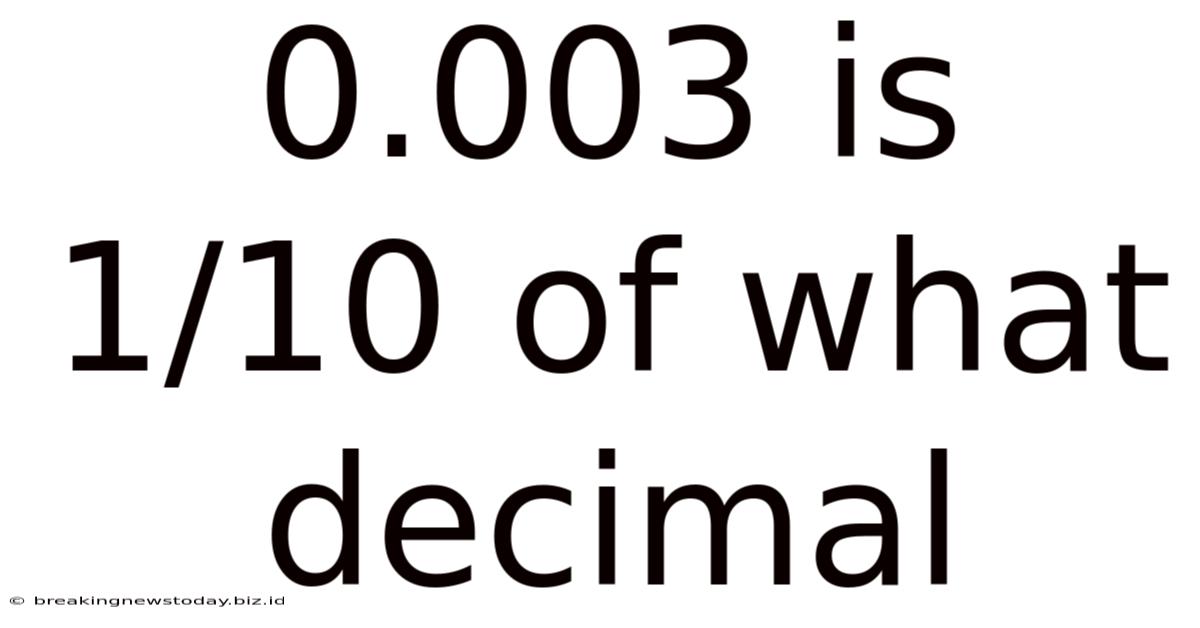
Table of Contents
0.003 is 1/10 of What Decimal? Unraveling Decimal Relationships
Understanding decimal relationships is crucial for various mathematical applications, from simple calculations to complex data analysis. This article delves into the question, "0.003 is 1/10 of what decimal?" providing a comprehensive explanation with practical examples and related concepts. We'll explore the underlying principles, demonstrate the solution, and offer further insights into working with decimals. This will equip you with the knowledge to confidently tackle similar problems and enhance your understanding of decimal arithmetic.
Understanding Decimals and Fractions
Before we dive into the solution, let's refresh our understanding of decimals and fractions. Decimals are a way of representing numbers that are not whole numbers. They use a decimal point to separate the whole number part from the fractional part. For example, in the decimal 2.5, '2' is the whole number part, and '.5' represents the fractional part, which is equivalent to one-half (1/2).
Fractions, on the other hand, represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, and the denominator indicates the total number of parts the whole is divided into. For instance, 1/4 represents one part out of four equal parts.
Decimals and fractions are interchangeable. You can easily convert a fraction to a decimal by dividing the numerator by the denominator. Similarly, you can convert a decimal to a fraction by writing the decimal as a fraction with a power of 10 as the denominator and then simplifying the fraction.
Solving the Problem: 0.003 is 1/10 of What Decimal?
The problem states that 0.003 is one-tenth (1/10) of an unknown decimal. We can express this relationship mathematically as:
0.003 = (1/10) * x
Where 'x' represents the unknown decimal we need to find.
To solve for 'x', we can follow these steps:
- Multiply both sides by 10: This will eliminate the fraction (1/10) from the equation.
0.003 * 10 = (1/10) * x * 10 - Simplify:
0.03 = x
Therefore, 0.003 is one-tenth of 0.03.
Verifying the Solution
We can verify our solution by checking if 0.003 is indeed 1/10 of 0.03. We can do this by multiplying 0.03 by 1/10 (or dividing 0.03 by 10):
0.03 * (1/10) = 0.03 / 10 = 0.003
This confirms that our solution is correct.
Expanding the Understanding: Decimal Place Values
A strong understanding of decimal place values is vital when working with decimals. Each position to the right of the decimal point represents a decreasing power of 10.
- Tenths (1/10): The first digit after the decimal point represents tenths.
- Hundredths (1/100): The second digit represents hundredths.
- Thousandths (1/1000): The third digit represents thousandths.
- Ten-thousandths (1/10000): The fourth digit represents ten-thousandths and so on.
Understanding these place values allows you to easily convert between decimals and fractions and perform calculations with decimals efficiently. For example, 0.003 can be expressed as 3/1000 because the '3' is in the thousandths place.
Practical Applications
The ability to understand and solve problems involving decimal relationships is crucial in various real-world scenarios:
- Finance: Calculating percentages, interest rates, and discounts often involves working with decimals.
- Science: Many scientific measurements and calculations utilize decimals, especially in fields like chemistry and physics.
- Engineering: Precision engineering relies heavily on accurate decimal calculations.
- Data Analysis: Statistical analysis often involves working with large datasets containing decimal numbers.
- Everyday Life: Calculating tips, splitting bills, or measuring quantities often involve decimals.
Related Concepts and Further Exploration
This section explores related concepts that build upon the understanding of decimal relationships:
1. Multiplying and Dividing Decimals by Powers of 10
Multiplying a decimal by a power of 10 (10, 100, 1000, etc.) simply moves the decimal point to the right by the number of zeros in the power of 10. Dividing by a power of 10 moves the decimal point to the left. This is a quick and efficient method for performing these calculations.
2. Converting Decimals to Fractions and Vice Versa
As mentioned earlier, decimals and fractions are interchangeable. Converting between the two is a fundamental skill in mathematics. Remember that the position of each digit after the decimal point determines the denominator of the equivalent fraction.
3. Working with Percentages
Percentages are essentially fractions expressed as a portion of 100. Understanding decimal relationships is crucial for converting between percentages and decimals (and fractions). To convert a percentage to a decimal, divide by 100 (or move the decimal point two places to the left). To convert a decimal to a percentage, multiply by 100 (or move the decimal point two places to the right).
4. Decimal Approximation and Rounding
Often, you'll need to round decimals to a specific number of decimal places. This is essential for simplifying calculations and presenting results in a clear and concise manner. Rounding rules dictate whether to round up or down based on the digit immediately following the desired decimal place.
Conclusion: Mastering Decimal Relationships
Understanding the relationship between decimals is fundamental to mathematical proficiency and has widespread applications in various fields. This article explored the problem "0.003 is 1/10 of what decimal?" demonstrating the solution and expanding on related concepts such as decimal place values, converting between decimals and fractions, and working with percentages. By mastering these concepts, you'll significantly enhance your numerical skills and problem-solving abilities in various mathematical and real-world contexts. Remember to practice regularly and apply these concepts in various scenarios to strengthen your understanding and improve your fluency with decimals.
Latest Posts
Latest Posts
-
Why Was The Painting Above Not Well Received
Jun 08, 2025
-
Given Abc Xyz What Is The Value Of Cos Z
Jun 08, 2025
-
If An Effective Price Ceiling Is Placed On Hamburgers Then
Jun 08, 2025
-
In Order To Resist Corrosion In Wet Environments Emt Is
Jun 08, 2025
-
For Each Pair Of Triangles State The Postulate Or Theorem
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about 0.003 Is 1/10 Of What Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.