0.008 Is 1/10 Of What Decimal
Breaking News Today
Jun 07, 2025 · 5 min read
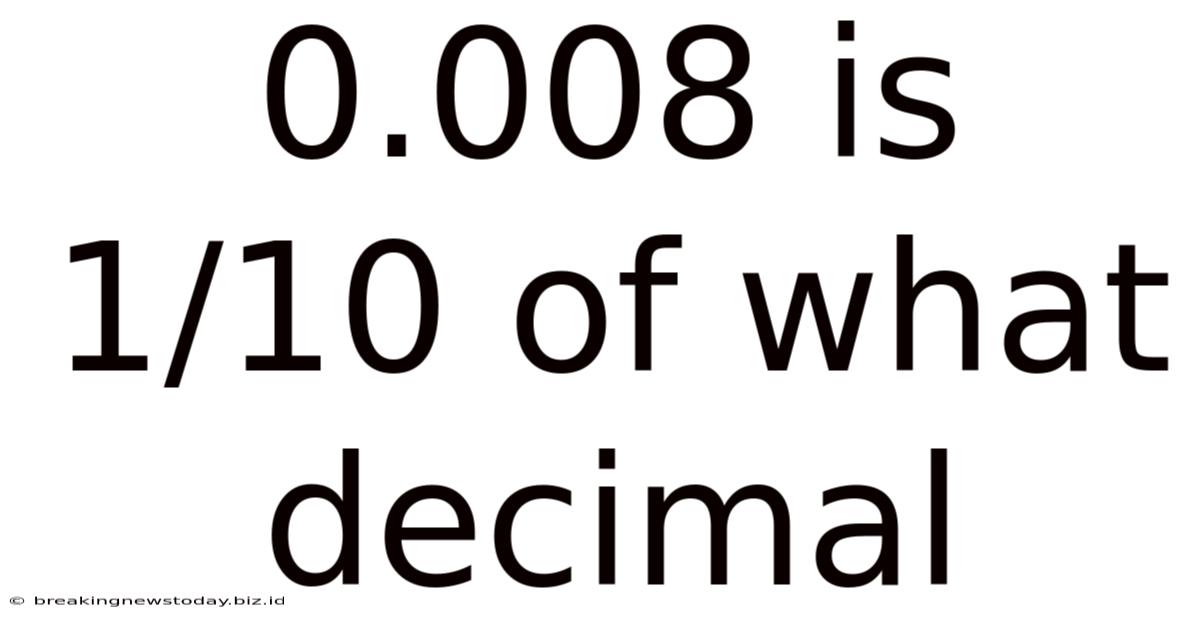
Table of Contents
0.008 is 1/10 of What Decimal? Unraveling the Mystery of Decimal Division
This seemingly simple question, "0.008 is 1/10 of what decimal?", delves into the fundamental principles of decimal arithmetic and proportional reasoning. Understanding how to solve this problem not only provides the answer but also builds a stronger foundation for tackling more complex mathematical challenges. We'll explore multiple approaches, from basic multiplication to more abstract proportional reasoning, ensuring a comprehensive understanding for all levels.
Understanding the Problem: Deconstructing the Question
The core of the problem lies in understanding the relationship between 0.008 and the unknown decimal. The phrase "1/10 of what decimal" implies a proportional relationship. In simpler terms, we're looking for a number (let's call it 'x') such that one-tenth of 'x' equals 0.008. This can be represented algebraically as:
(1/10) * x = 0.008
This equation forms the basis of our solution strategies.
Method 1: Solving through Direct Multiplication
The most straightforward approach is to isolate 'x' in the equation above. To do this, we need to eliminate the (1/10) fraction multiplying 'x'. We can achieve this by multiplying both sides of the equation by 10:
10 * (1/10) * x = 0.008 * 10
This simplifies to:
x = 0.08
Therefore, 0.008 is 1/10 of 0.08.
This method emphasizes the direct relationship between the given decimal and the unknown decimal, highlighting the essence of the problem in a clear and concise manner. It's a perfect method for beginners looking to grasp the core concepts.
Method 2: Applying Proportional Reasoning
Proportional reasoning offers a more intuitive understanding of the relationship between the numbers. We can set up a proportion to solve for the unknown decimal:
0.008 / x = 1/10
This proportion states that the ratio of 0.008 to the unknown decimal (x) is equal to the ratio of 1 to 10. To solve for x, we can cross-multiply:
0.008 * 10 = 1 * x
This simplifies to:
0.08 = x
Again, we arrive at the solution: x = 0.08. This method provides a more conceptual understanding of the problem, emphasizing the proportional relationship between the known and unknown quantities. It is useful in scenarios where the relationship between quantities is crucial for understanding the overall concept.
Method 3: Understanding Decimal Place Values
This approach utilizes the understanding of decimal place values. Since 0.008 is one-tenth of the unknown decimal, we can visualize the movement of the decimal point. Multiplying by 10 is essentially moving the decimal point one place to the right. If 0.008 is 1/10th of the unknown value, then the unknown value must be obtained by moving the decimal place one position to the right. This directly gives us:
0.08
This method emphasizes the visual representation of decimal multiplication and division, reinforcing the understanding of place value. This approach offers a quick, intuitive way to solve the problem and is particularly helpful for developing a strong grasp of decimal manipulation.
Extending the Understanding: Exploring Similar Problems
Understanding this basic problem opens the door to solving more complex variations. Consider these examples:
-
0.0008 is 1/100 of what decimal? Applying the same principles, we multiply 0.0008 by 100, moving the decimal point two places to the right, yielding 0.08.
-
What is 1/1000 of 0.8? Here, we divide 0.8 by 1000, effectively moving the decimal point three places to the left, resulting in 0.0008.
These examples demonstrate the adaptability of the methods discussed previously. The core principles of multiplication, division, proportional reasoning, and understanding decimal place values remain consistent, allowing for the solution of a wide range of similar problems.
Practical Applications: Real-World Scenarios
Understanding decimal proportions is crucial in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, and tax percentages often involves manipulating decimals.
-
Engineering: Precise measurements and calculations frequently rely on understanding decimal relationships.
-
Science: Many scientific concepts involve proportional relationships expressed as decimals.
-
Everyday Life: Simple tasks like calculating tips, splitting bills, or converting units often involve manipulating decimals and percentages.
Mastering these foundational concepts significantly improves problem-solving skills in these diverse contexts.
Boosting Mathematical Proficiency: Beyond the Basics
While this problem seems elementary, it serves as a gateway to more advanced mathematical concepts. The ability to confidently manipulate decimals and solve proportional relationships is essential for:
-
Algebra: Solving equations and inequalities often requires understanding decimals and their relationships.
-
Calculus: Derivatives and integrals often involve manipulating decimals and understanding rates of change.
-
Statistics: Data analysis and interpretation frequently involve working with decimal values.
Strong foundational skills in decimal arithmetic pave the way for success in these higher-level mathematical disciplines.
Conclusion: Mastering Decimals, Mastering Opportunities
Solving the problem, "0.008 is 1/10 of what decimal?", is more than just finding the answer (0.08). It's about understanding the underlying principles of decimal arithmetic, proportional reasoning, and place value. By mastering these concepts, you not only develop stronger problem-solving skills but also open doors to more advanced mathematical concepts and a broader range of real-world applications. The journey from a seemingly simple question to a deeper understanding of mathematical principles highlights the importance of foundational knowledge and its far-reaching implications. So, the next time you encounter a decimal problem, remember the multifaceted approaches discussed here – they're your key to unlocking mathematical proficiency and success. The ability to confidently manipulate decimals will undoubtedly prove invaluable in your academic and professional pursuits.
Latest Posts
Latest Posts
-
How Many Valence Electrons Are In The Trimethylammonium Ion
Jun 07, 2025
-
Cu L Es La Actividad Favorita De Karina
Jun 07, 2025
-
Amoebas Prey Upon Algae In Aquatic Environments
Jun 07, 2025
-
An Employee Quits His Job And Converts His Group Policy
Jun 07, 2025
-
Round 845 001 To The Nearest Thousand
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 0.008 Is 1/10 Of What Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.