0.09 10 Times As Much As
Breaking News Today
Jun 06, 2025 · 5 min read
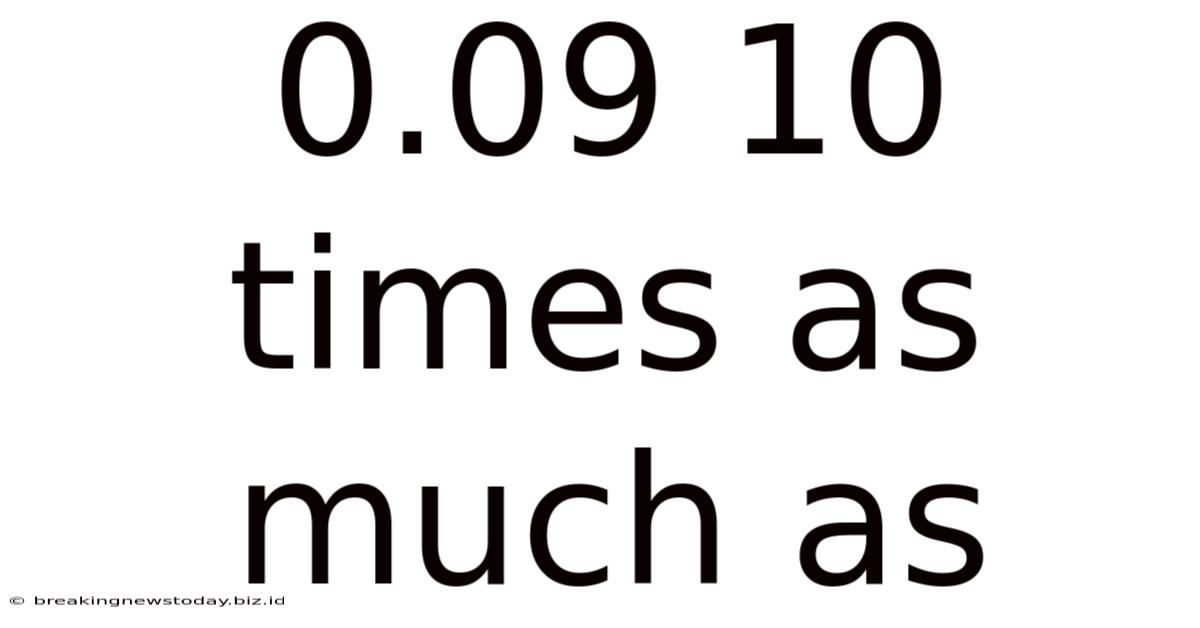
Table of Contents
0.09: Ten Times the Magnitude and its Implications
This article delves into the mathematical concept of multiplying a decimal number, specifically 0.09, by 10. We'll explore the process, its implications in various contexts, and the broader mathematical principles involved. Understanding this seemingly simple calculation is fundamental to grasping more complex mathematical operations and real-world applications.
Understanding Decimal Multiplication
Before we tackle the specific problem of multiplying 0.09 by 10, let's review the basics of decimal multiplication. Decimals represent fractions where the denominator is a power of 10 (e.g., 10, 100, 1000). Multiplying a decimal by 10 involves shifting the decimal point one place to the right. This is because multiplying by 10 is the same as multiplying by 10/1, which effectively increases the value of the number by a factor of 10.
Calculating 0.09 x 10
Now, let's perform the calculation: 0.09 x 10. Following the rule of shifting the decimal point one place to the right, we get:
0.09 x 10 = 0.9
This simple calculation demonstrates a fundamental concept in mathematics: the effect of multiplying by powers of 10. Let's expand upon this concept to solidify our understanding.
Expanding the Concept: Powers of 10 and Decimal Shifts
Multiplying by powers of 10 consistently shifts the decimal point to the right:
- Multiplying by 10: Shifts the decimal point one place to the right.
- Multiplying by 100: Shifts the decimal point two places to the right.
- Multiplying by 1000: Shifts the decimal point three places to the right.
Conversely, dividing by powers of 10 shifts the decimal point to the left:
- Dividing by 10: Shifts the decimal point one place to the left.
- Dividing by 100: Shifts the decimal point two places to the left.
- Dividing by 1000: Shifts the decimal point three places to the left.
Understanding this pattern is crucial for quick mental calculations and for efficient problem-solving in various mathematical contexts.
Real-World Applications: From Finance to Science
The seemingly simple multiplication of 0.09 by 10 has numerous real-world applications across various disciplines:
-
Finance: Imagine calculating interest on an investment or a loan. If the interest rate is 0.09 (9%) per annum, multiplying by 10 gives you the interest earned or owed after 10 years, assuming a consistent interest rate. This basic calculation forms the foundation of more complex financial models. Understanding percentage increases and decreases, fundamental in finance, relies on similar principles.
-
Science: In scientific measurements, especially those involving very small quantities, decimals are common. Converting units of measurement often involves multiplying or dividing by powers of 10. For example, converting milligrams to grams requires dividing by 1000, while converting centimeters to meters requires dividing by 100. The principles discussed earlier are directly applicable in these scenarios. Scientific notation, extensively used in physics and chemistry, depends heavily on understanding powers of 10.
-
Engineering: Engineering designs often involve precise calculations, and decimals are essential. Scaling designs up or down involves multiplying or dividing dimensions by factors that are often powers of 10. This ensures consistency and accuracy in the construction or production processes.
-
Everyday Life: Even everyday tasks might involve multiplying or dividing decimals. Calculating discounts (e.g., 10% off), working with recipes that require fractional measurements, or dividing costs among friends all involve working with decimals and understanding their manipulation.
Beyond 0.09 x 10: Extending the Principles
The principles explored with 0.09 x 10 can be extended to encompass a wide range of decimal numbers and multipliers. The core concept remains consistent: multiplying by a power of 10 shifts the decimal point to the right, while dividing shifts it to the left. This understanding is fundamental to mastering more advanced mathematical concepts.
Connecting to Other Mathematical Concepts
The simple operation of 0.09 x 10 connects to several other important mathematical concepts:
-
Fractions and Decimals: Understanding the relationship between fractions and decimals is crucial. 0.09 is equivalent to the fraction 9/100. Multiplying this fraction by 10 yields 90/100, which simplifies to 9/10 or 0.9. This illustrates the equivalence and interchangeability of fractions and decimals.
-
Scientific Notation: Scientific notation is a concise way to represent very large or very small numbers. It uses powers of 10. Understanding the manipulation of decimals with powers of 10 is directly relevant to working with scientific notation.
-
Logarithms: Logarithms are related to exponents and powers. The principles learned here regarding powers of 10 are foundational to understanding logarithms.
Practical Exercises for Enhanced Understanding
To solidify your understanding, try these exercises:
- Calculate 0.005 x 100.
- Calculate 2.75 x 10.
- Calculate 15.3 / 1000.
- Convert 0.00075 meters to millimeters.
- A recipe calls for 0.25 liters of milk. How much milk is needed if you triple the recipe?
Working through these exercises will reinforce your comprehension of decimal multiplication and division by powers of 10.
Conclusion: The Significance of a Simple Calculation
The seemingly straightforward calculation of 0.09 multiplied by 10 illustrates a fundamental principle in mathematics with far-reaching consequences. Understanding this principle is essential for navigating various mathematical operations, interpreting data, and solving problems across numerous disciplines, from finance and science to engineering and everyday life. The ability to confidently manipulate decimals and powers of 10 is a crucial skill for anyone seeking to develop strong mathematical literacy. This seemingly simple operation acts as a building block for more advanced mathematical concepts and problem-solving strategies. By mastering this foundation, you'll enhance your mathematical capabilities and open doors to a more profound understanding of the numerical world around us.
Latest Posts
Latest Posts
-
Deconstruct The Word Epidermis Enter Hyphens In The Appropriate Blanks
Jun 07, 2025
-
Ms Hernandez Has 17 Tomato Plants
Jun 07, 2025
-
Given The Venn Diagram Below What Is The Correct Notation
Jun 07, 2025
-
Which Of The Following Is A Quality Of A Feeler
Jun 07, 2025
-
600 Is How Many Times As Much As 2
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 0.09 10 Times As Much As . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.