0.09 Is 10 Times As Much As
Breaking News Today
Jun 07, 2025 · 5 min read
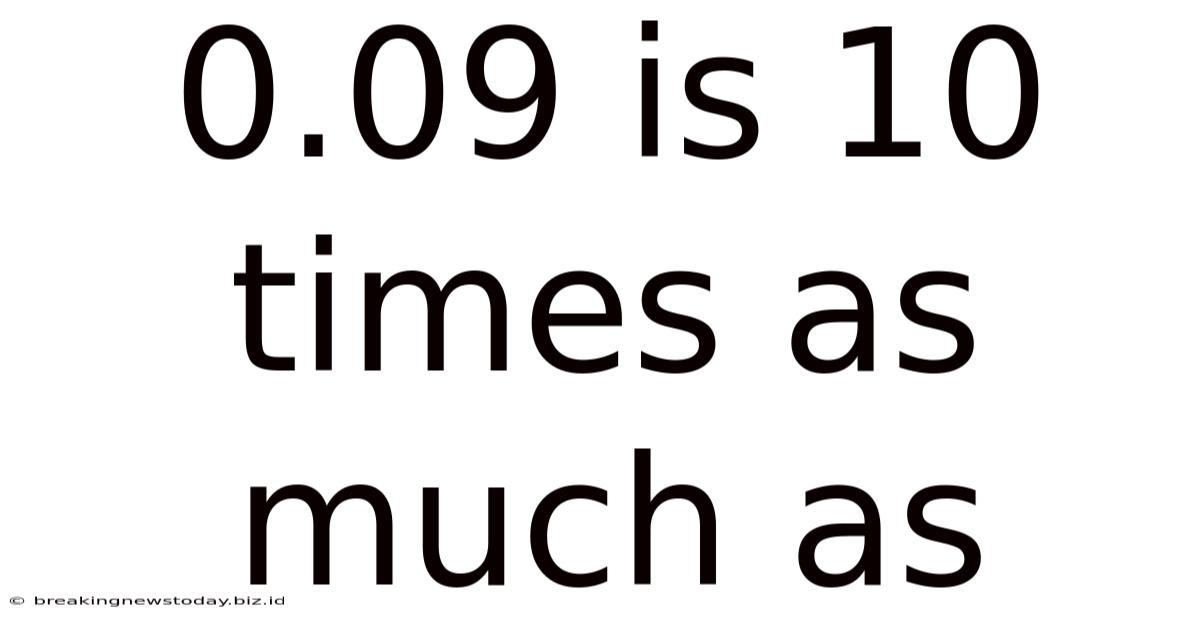
Table of Contents
0.09 is 10 Times as Much as: Understanding Decimal Relationships
Understanding decimal relationships is crucial for mastering mathematics and excelling in various fields. This article delves deep into the concept of decimal multiplication and division, focusing on the statement "0.09 is 10 times as much as." We will explore this relationship using multiple approaches, providing a comprehensive understanding for learners of all levels.
Decimals: A Quick Refresher
Before we dive into the core concept, let's briefly revisit the fundamentals of decimals. Decimals are a way of representing numbers that are not whole numbers. They use a decimal point to separate the whole number part from the fractional part. The digits to the right of the decimal point represent fractions of a whole. For example, in the number 0.09, the '0' before the decimal represents the whole number portion (in this case, zero), while '09' represents nine hundredths (9/100).
Each position to the right of the decimal point represents a decreasing power of 10:
- 0.1 represents one-tenth (1/10)
- 0.01 represents one-hundredth (1/100)
- 0.001 represents one-thousandth (1/1000)
- and so on...
Exploring the Relationship: 0.09 and 0.009
The statement "0.09 is 10 times as much as" implies a multiplication relationship. To find the number that is 10 times smaller than 0.09, we need to perform division. The solution is found by dividing 0.09 by 10:
0.09 ÷ 10 = 0.009
Therefore, 0.09 is 10 times as much as 0.009.
Visualizing the Relationship
Understanding this relationship can be easier with visual aids. Imagine you have 9 blocks representing 0.09. If you divide those 9 blocks into 10 equal groups, each group would contain 0.9 blocks. But since you can't have fractions of a block, we need to look at the problem differently in terms of hundredths.
If we represent 0.09 as 9 hundredths, and divide these 9 hundredths into 10 equal groups, each group would contain 0.9 hundredths or 9 thousandths (0.009).
Mathematical Explanation: Moving the Decimal Point
Multiplying and dividing decimals by powers of 10 involves a simple trick: moving the decimal point.
- Multiplying by 10: Move the decimal point one place to the right. For example, 0.009 x 10 = 0.09.
- Dividing by 10: Move the decimal point one place to the left. For example, 0.09 ÷ 10 = 0.009.
This method is particularly useful for quick calculations and reinforces the understanding of decimal place values.
Practical Applications: Real-World Examples
Understanding decimal relationships is not just a theoretical exercise; it has numerous practical applications in everyday life. Here are some examples:
- Finance: Calculating percentages, interest rates, discounts, and tax amounts often involve decimal operations. For instance, calculating 10% of a price requires dividing the price by 10.
- Measurements: Converting units of measurement frequently involves decimal manipulation. For example, converting centimeters to meters (100 centimeters in 1 meter) or millimeters to centimeters (10 millimeters in 1 centimeter).
- Science: Scientific measurements often involve decimals, requiring accurate calculations involving multiplication and division of decimals.
- Engineering: Precise calculations and scaling in engineering projects rely heavily on a robust understanding of decimals.
Expanding the Concept: Beyond 10
Let's extend our understanding beyond multiplication and division by 10. Consider these scenarios:
- 0.09 is 100 times as much as: To find the answer, we divide 0.09 by 100. This involves moving the decimal point two places to the left, resulting in 0.0009.
- 0.09 is 1000 times as much as: Dividing 0.09 by 1000 (moving the decimal point three places to the left), we get 0.00009.
- 0.09 is 1/10 as much as: Multiplying 0.09 by 1/10 is equivalent to dividing it by 10. As we've seen, this gives us 0.009.
- 0.09 is 1/100 as much as: Multiplying 0.09 by 1/100 is equivalent to dividing it by 100, resulting in 0.0009.
These examples illustrate how multiplying or dividing by powers of 10 systematically shifts the decimal point, providing a straightforward method for solving these types of problems.
Tackling More Complex Scenarios
Let's consider scenarios that incorporate this knowledge into more complex problems:
Scenario 1: If a recipe calls for 0.09 liters of milk, and you want to make a recipe that is 10 times larger, how much milk do you need?
Solution: Multiply 0.09 liters by 10. This equals 0.9 liters of milk.
Scenario 2: A small plot of land measures 0.009 square kilometers. A larger plot is 100 times bigger. What is the area of the larger plot?
Solution: Multiply 0.009 square kilometers by 100. This equals 0.9 square kilometers.
Scenario 3: A scientist measures 0.9 grams of a substance. Another sample is 1/10 the size. What is the weight of the smaller sample?
Solution: Divide 0.9 grams by 10. This equals 0.09 grams.
Strengthening Your Understanding: Practice Exercises
To solidify your understanding of decimal relationships, try these practice problems:
- 0.0007 is 10 times as much as what number?
- What number is 100 times smaller than 0.6?
- If a bag of flour weighs 0.75 kilograms, how much would 10 bags weigh?
- A container holds 0.05 liters of liquid. How much liquid is in 100 such containers?
- A piece of wood measures 0.002 meters. What is the length of 1000 pieces laid end-to-end?
Conclusion: Mastering Decimal Relationships
Understanding the relationship between decimals, particularly involving multiplication and division by powers of 10, is a fundamental skill in mathematics. By grasping the concept of moving the decimal point and applying it to practical scenarios, you can significantly improve your problem-solving abilities in various fields. Regular practice and application of this knowledge will build confidence and mastery of decimal operations. Remember the core principle: multiplying by powers of 10 moves the decimal point to the right, while dividing by powers of 10 moves it to the left. With this understanding, you can tackle more complex problems and confidently navigate the world of decimals.
Latest Posts
Latest Posts
-
8 51 Is What Percent Of 18 5
Jun 07, 2025
-
Additional Practice 1 4 Round Whole Numbers
Jun 07, 2025
-
Which Best Describes The Purpose Of This Prologue Excerpt
Jun 07, 2025
-
Specimen Labels Should Include All Of The Following Except
Jun 07, 2025
-
Tonya Has Replaced Her Whole Life
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 0.09 Is 10 Times As Much As . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.