0.6 Divided By 10 To The Power Of 2
Breaking News Today
Jun 08, 2025 · 5 min read
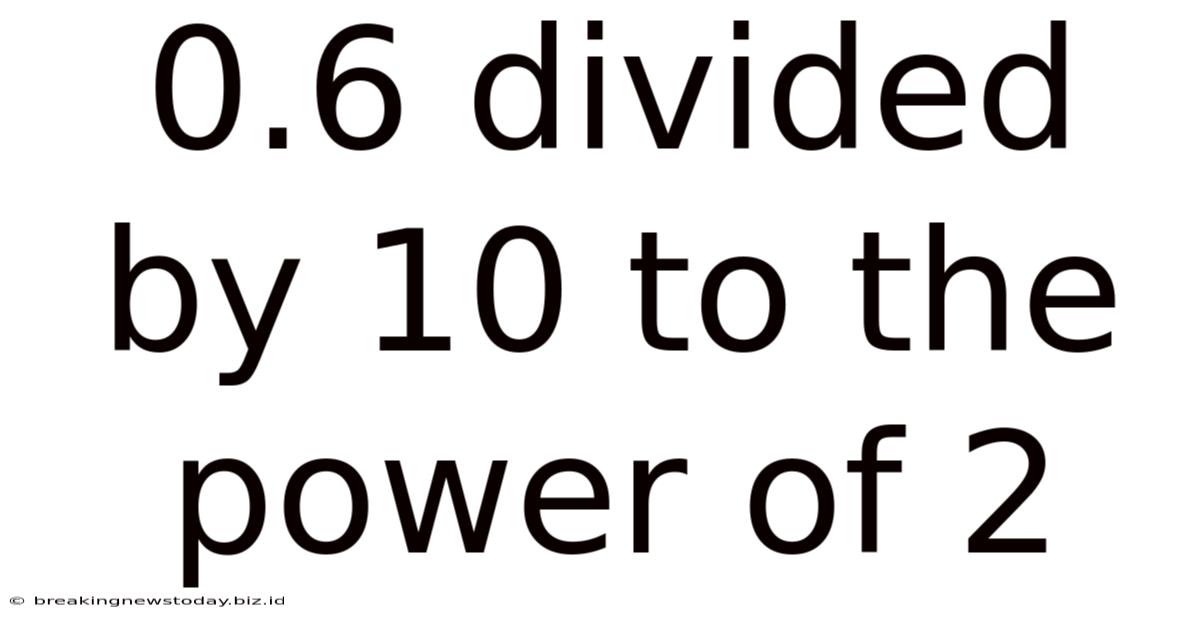
Table of Contents
Unpacking 0.6 Divided by 10 to the Power of 2: A Deep Dive into Decimal Division and Exponential Notation
This article delves into the seemingly simple calculation of 0.6 divided by 10 to the power of 2 (10²), exploring the underlying mathematical principles, different approaches to solving the problem, and expanding on the broader concepts of decimal division and exponential notation. We'll unpack this problem to reveal its intricacies and demonstrate how a basic calculation can illuminate fundamental mathematical ideas.
Understanding the Problem: 0.6 ÷ 10²
At its core, the problem asks us to divide the decimal number 0.6 by 100 (since 10² = 10 x 10 = 100). This involves understanding how decimals behave under division, particularly when the divisor is a power of 10. The seemingly simple nature of this problem belies its importance in grasping core mathematical concepts that extend far beyond basic arithmetic.
Method 1: Direct Decimal Division
The most straightforward approach is to perform the division directly. We can represent 0.6 as a fraction: 6/10. Therefore, the problem becomes:
(6/10) ÷ 100
To divide fractions, we invert the second fraction and multiply:
(6/10) x (1/100) = 6/1000
Now, converting this fraction back to a decimal, we get:
6/1000 = 0.006
This method highlights the fundamental process of decimal division and the relationship between fractions and decimals.
Method 2: Utilizing Exponential Properties
This method leverages the properties of exponents to simplify the calculation. We can rewrite the problem as:
0.6 ÷ 10²
Remember that dividing by 10² is the same as multiplying by 10⁻². This stems from the rule of negative exponents: a⁻ⁿ = 1/aⁿ. Therefore, we have:
0.6 x 10⁻²
Now, recall that multiplying a decimal by 10⁻² (or 0.01) moves the decimal point two places to the left. Applying this rule:
0.6 x 10⁻² = 0.006
This approach showcases the power and elegance of exponential notation in simplifying calculations involving powers of 10. It also underscores the interconnectedness of seemingly disparate mathematical concepts.
Method 3: Scientific Notation
Scientific notation provides another elegant solution. First, we express 0.6 in scientific notation:
0.6 = 6 x 10⁻¹
Now, substitute this into our original problem:
(6 x 10⁻¹) ÷ 10²
Using the rule of exponent division (aᵐ ÷ aⁿ = aᵐ⁻ⁿ), we simplify:
6 x 10⁻¹⁻² = 6 x 10⁻³
Converting this back to standard decimal form:
6 x 10⁻³ = 0.006
This method emphasizes the efficiency and precision offered by scientific notation, particularly when dealing with very large or very small numbers. It also reinforces the understanding of exponent rules in a practical context.
Expanding on Decimal Division
Decimal division forms a crucial part of many mathematical applications, from everyday financial calculations to advanced scientific computations. Understanding its intricacies is crucial for developing a strong mathematical foundation.
Key Concepts in Decimal Division:
- Place Value: A solid grasp of place value is paramount. Understanding the value of each digit based on its position (ones, tenths, hundredths, etc.) is essential for performing accurate decimal division.
- Long Division: While calculators are readily available, understanding the process of long division provides a deeper understanding of the underlying principles of division.
- Estimation: Before performing the calculation, estimating the approximate result helps verify the reasonableness of the final answer. This prevents errors and builds confidence in the result.
- Recurring Decimals: In some cases, decimal division results in recurring (repeating) decimals. Knowing how to represent these using appropriate notation is vital.
Exploring Exponential Notation
Exponential notation, also known as scientific notation or standard form, is a powerful tool for representing numbers, especially those that are extremely large or small. It's based on the concept of powers of 10.
Key aspects of Exponential Notation:
- Base and Exponent: The base (usually 10) is raised to a specific power (the exponent). The exponent indicates how many times the base is multiplied by itself.
- Positive and Negative Exponents: Positive exponents denote large numbers, while negative exponents represent small numbers (fractions).
- Scientific Notation: This is a specific form of exponential notation where the number is written as a value between 1 and 10 multiplied by a power of 10.
Real-World Applications
The principles demonstrated in this problem – decimal division and exponential notation – find applications in a wide variety of fields:
- Finance: Calculating interest, discounts, and loan repayments often involves decimal division and understanding percentages, which are directly related to decimals and fractions.
- Science: Many scientific measurements involve extremely large or small numbers. Exponential notation is essential for representing these quantities, such as the distance between stars or the size of atoms.
- Engineering: Engineers use decimal division and exponential notation extensively in calculations related to dimensions, measurements, and scaling of designs.
- Computer Science: Representing numbers within computer systems often utilizes similar concepts to exponential notation.
Further Exploration and Practice
To solidify your understanding, consider these exercises:
- Calculate 0.08 divided by 10³.
- Express the number 250,000,000 in scientific notation.
- Convert 3.45 x 10⁻⁵ to standard decimal form.
- Solve (7.2 x 10⁴) ÷ (2.4 x 10²).
- Explain the difference between 10² and 10⁻².
By working through these examples, you will strengthen your skills in decimal division, exponential notation, and scientific notation, enhancing your mathematical capabilities and problem-solving skills. This foundational knowledge extends beyond simple calculations, building a solid base for more complex mathematical and scientific endeavors. Understanding the relationship between these concepts allows for a more intuitive and efficient approach to solving a wide range of numerical problems. This exploration demonstrates that even seemingly straightforward calculations can lead to a deeper appreciation of the beauty and interconnectedness of mathematical principles.
Latest Posts
Related Post
Thank you for visiting our website which covers about 0.6 Divided By 10 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.