0.75 X 20 2 0.5 X 2
Breaking News Today
Jun 04, 2025 · 5 min read
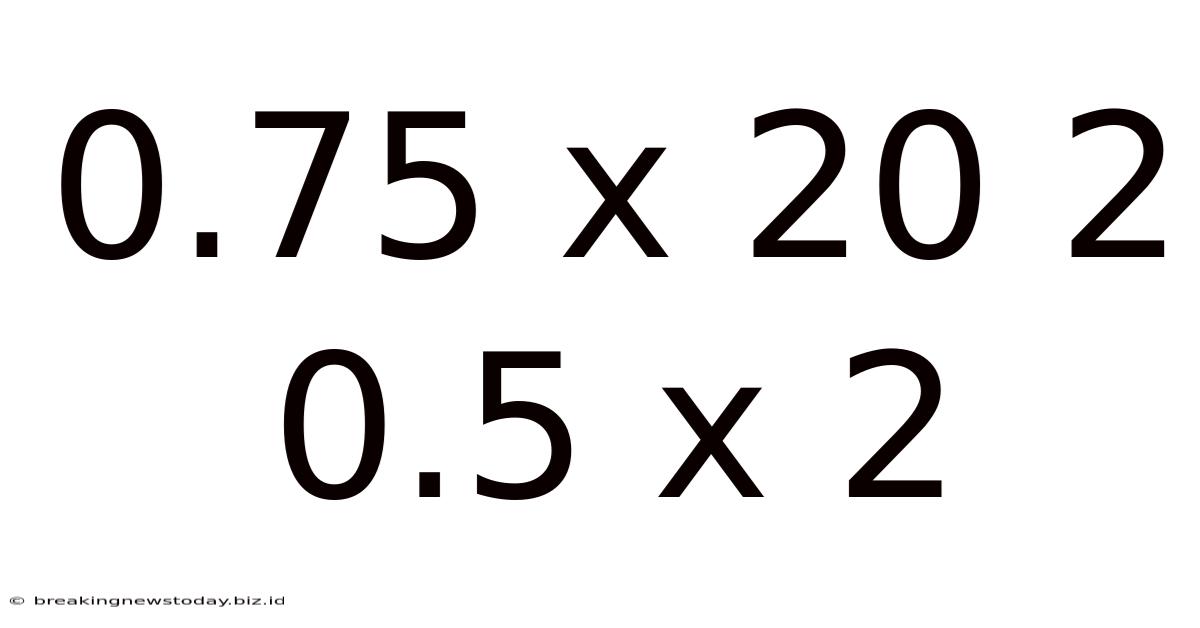
Table of Contents
Decoding 0.75 x 20 + 0.5 x 2: A Deep Dive into Mathematical Operations and Their Applications
This seemingly simple mathematical expression, 0.75 x 20 + 0.5 x 2, offers a fascinating gateway to exploring fundamental arithmetic operations, their practical applications across various fields, and the importance of order of operations (PEMDAS/BODMAS). This article will dissect the calculation step-by-step, explore the underlying concepts, and demonstrate how similar calculations are used in diverse real-world scenarios.
Understanding the Components: Decimals and Fractions
Before diving into the calculation, let's refresh our understanding of decimals and fractions. The expression involves decimals (0.75 and 0.5), which represent parts of a whole. 0.75 is equivalent to ¾ (three-quarters) and 0.5 is equivalent to ½ (one-half). Understanding this equivalence is crucial, as it allows for flexible manipulation and application of the problem in different contexts.
Applying the Order of Operations (PEMDAS/BODMAS)
The acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) dictates the order in which mathematical operations should be performed. In this case, multiplication comes before addition.
Step 1: Multiplication
First, we perform the multiplications:
- 0.75 x 20 = 15
- 0.5 x 2 = 1
Step 2: Addition
Next, we add the results of the multiplications:
- 15 + 1 = 16
Therefore, the solution to 0.75 x 20 + 0.5 x 2 is 16.
Real-World Applications: Where This Calculation Might Appear
While this might seem like a simple arithmetic problem, the principles involved are foundational to countless real-world applications. Let's explore some examples:
1. Finance and Budgeting:
Imagine you're calculating the total cost of items. Suppose you buy 20 units of a product costing $0.75 each and 2 units of another product costing $0.50 each. The calculation 0.75 x 20 + 0.5 x 2 directly gives you the total cost. This type of calculation is fundamental in personal finance, business accounting, and even larger-scale financial modeling.
2. Construction and Engineering:
In construction, calculations involving decimals and fractions are commonplace. Consider calculating the total length of materials needed for a project. If a section requires 20 pieces of lumber, each 0.75 meters long, and another section needs 2 pieces of a different type of lumber, each 0.5 meters long, the total length would be calculated using the same principle: 0.75 x 20 + 0.5 x 2 = 16 meters. This is a simplified example, but it illustrates the relevance of such calculations in larger-scale engineering projects.
3. Science and Measurement:
Scientific experiments and data analysis often involve decimal values and calculations. Imagine measuring the volume of liquids in a chemistry experiment. If you have 20 samples of a solution, each with a volume of 0.75 liters, and 2 samples of another solution, each with a volume of 0.5 liters, the total volume would be 16 liters, calculated using the same formula. This simple calculation underlies more complex scientific modeling and data analysis.
4. Everyday Life:
Even seemingly mundane activities involve similar calculations. Imagine you are baking a cake and the recipe calls for 0.75 cups of sugar for one part and 0.5 cups of sugar for another. If you want to double one part of the recipe, you'll need to perform this exact calculation. The ability to perform these calculations quickly and accurately ensures success in the kitchen.
Expanding the Concepts: Variations and Extensions
The basic calculation 0.75 x 20 + 0.5 x 2 can be extended and adapted in various ways to model more complex situations. Let's look at a few examples:
-
Introducing Variables: Instead of fixed numbers, we could use variables. For example, let 'x' represent the cost per unit and 'y' represent the number of units. The expression could become: (x * y) + (0.5 * 2). This allows for greater flexibility and the possibility of solving for different values of x and y.
-
Adding More Terms: We could extend the expression by adding more terms, for instance: 0.75 x 20 + 0.5 x 2 + 1.25 x 5. This would involve more multiplications and additions, but the same principles of order of operations would apply.
-
Using Fractions: We could rewrite the expression using fractions: (¾ * 20) + (½ * 2). This highlights the equivalence between decimals and fractions and allows for alternative calculation methods.
-
Introducing Parentheses/Brackets: Parentheses or brackets can change the order of operations. For example, (0.75 x 20) + (0.5 x 2) is the same as the original expression, but (0.75 x (20 + 0.5)) x 2 would produce a different result. This emphasizes the importance of understanding and correctly applying the order of operations.
Importance of Accuracy and Precision
In many real-world applications, the accuracy and precision of calculations are paramount. In financial transactions, for example, even small errors can have significant consequences. Similarly, in engineering and scientific contexts, inaccuracies can lead to design flaws or experimental errors. Understanding the fundamentals of arithmetic and using appropriate calculation methods are therefore crucial to ensuring accuracy and precision.
Beyond the Calculation: Developing Mathematical Skills
The seemingly simple calculation 0.75 x 20 + 0.5 x 2 serves as a valuable stepping stone to developing stronger mathematical skills. The ability to perform these calculations accurately and efficiently is essential for success in various academic and professional fields. Furthermore, understanding the underlying principles of arithmetic strengthens critical thinking and problem-solving skills, which are transferable to many aspects of life.
Conclusion: The Power of Simple Arithmetic
While the expression 0.75 x 20 + 0.5 x 2 might appear trivial at first glance, it embodies fundamental mathematical concepts with wide-ranging applications. From managing personal finances to conducting scientific experiments, mastering basic arithmetic operations is crucial for navigating our increasingly complex world. By understanding the order of operations and applying these principles to various contexts, we can unlock the power of simple arithmetic to solve real-world problems and develop valuable skills for the future. The seemingly simple equation holds far more significance than its initial appearance suggests, illustrating the importance of foundational mathematical literacy in every aspect of life.
Latest Posts
Latest Posts
-
Which Two Statements About Redox Reactions Are True
Jun 06, 2025
-
Youve Been Assigned A Research Paper On The Holy Wars
Jun 06, 2025
-
What Is The Value Of Log Subscript 3 Baseline 81
Jun 06, 2025
-
Todos Los Cubanos Tienen Las Mismas Ra Ces Cierto Falso
Jun 06, 2025
-
5 Halves Plus 6 Halves Plus 3 Halves
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about 0.75 X 20 2 0.5 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.