0.8 Of What Number Is 6
Breaking News Today
Jun 04, 2025 · 5 min read
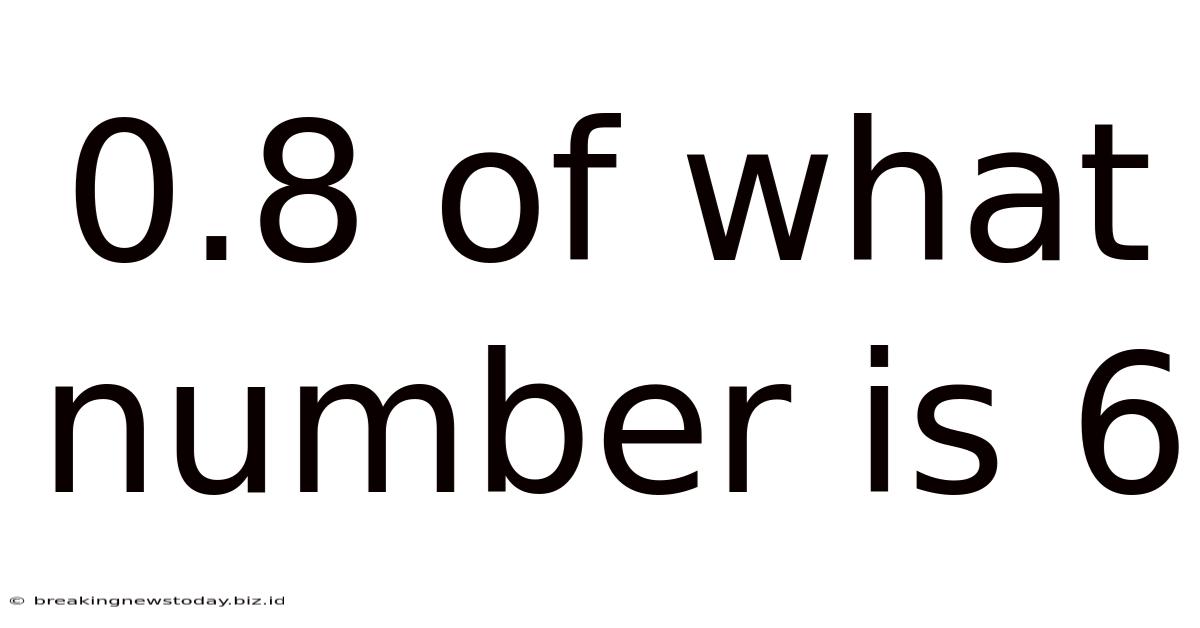
Table of Contents
0.8 of What Number is 6? Unraveling the Mystery of Percentages and Proportions
This seemingly simple question, "0.8 of what number is 6?", opens a door to a fascinating world of mathematics, specifically percentages, proportions, and algebraic problem-solving. It's a question that appears deceptively easy at first glance, but understanding its underlying principles allows us to tackle more complex problems with confidence. This article will delve deep into the solution, exploring various approaches and highlighting the practical applications of such calculations in everyday life.
Understanding the Problem: Deconstructing "0.8 of What Number is 6?"
Before diving into the solution, let's break down the problem into its constituent parts. The phrase "0.8 of what number is 6" translates mathematically into an equation:
0.8 * x = 6
Where:
- 0.8 represents the percentage (or fraction) we're dealing with – 80% expressed as a decimal.
- x represents the unknown number we are trying to find.
- 6 represents the result of taking 0.8 (or 80%) of the unknown number.
This equation forms the basis of our solution, and we'll explore several ways to solve for 'x'.
Method 1: Solving for x using Algebraic Manipulation
This method involves using basic algebraic principles to isolate 'x' and find its value. Here's how:
-
Start with the equation: 0.8 * x = 6
-
Isolate x: To isolate 'x', we need to divide both sides of the equation by 0.8:
x = 6 / 0.8
-
Perform the division: Dividing 6 by 0.8 gives us:
x = 7.5
Therefore, 0.8 of 7.5 is 6.
This method is straightforward and efficient, particularly when dealing with simple equations.
Method 2: Converting to Fractions for Easier Calculation
Sometimes, working with fractions can simplify the calculation, especially if you're dealing with percentages that easily convert to simple fractions. Let's see how:
-
Convert 0.8 to a fraction: 0.8 is equivalent to 8/10, which can be simplified to 4/5.
-
Rewrite the equation: The equation now becomes: (4/5) * x = 6
-
Isolate x: Multiply both sides of the equation by the reciprocal of 4/5, which is 5/4:
x = 6 * (5/4)
-
Perform the multiplication: This simplifies to:
x = 30/4
-
Simplify the fraction: Reducing the fraction to its simplest form gives:
x = 7.5
Again, we arrive at the same solution: x = 7.5. This method can be advantageous when dealing with percentages that translate to easily manageable fractions.
Method 3: Using the Percentage Formula
The percentage formula provides a structured approach to solving percentage problems. The formula is:
(Part / Whole) * 100% = Percentage
In our problem:
- Part = 6 (the result)
- Percentage = 80% (0.8 expressed as a percentage)
- Whole = x (the unknown number we are solving for)
Substituting these values into the formula:
(6 / x) * 100% = 80%
-
Simplify the equation: Divide both sides by 100%:
6 / x = 0.8
-
Isolate x: Cross-multiply to solve for x:
6 = 0.8x
-
Solve for x: Divide both sides by 0.8:
x = 6 / 0.8 = 7.5
This method reinforces the concept of percentage and provides a systematic approach to solving such problems, especially useful for those comfortable working with percentage formulas.
Practical Applications: Real-World Examples of Percentage Calculations
Understanding how to solve "0.8 of what number is 6" is not just an academic exercise. This type of calculation has widespread applications in various real-world scenarios, including:
-
Finance: Calculating discounts, interest rates, profit margins, and tax amounts. For example, if a store offers an 80% discount and an item is sold for $6, this calculation helps determine the original price.
-
Sales and Marketing: Analyzing sales figures, conversion rates, and market share. Determining the overall potential market size based on current sales is a practical use.
-
Science and Engineering: Analyzing experimental data, calculating proportions in chemical reactions, and scaling models. Proportionality and percentage calculations are fundamental in scientific research.
-
Everyday Life: Calculating tips, splitting bills, and determining portion sizes. From grocery shopping to restaurant bills, percentages are essential for managing personal finances.
Expanding the Concept: Tackling More Complex Percentage Problems
The principles learned from solving "0.8 of what number is 6" can be applied to more complex percentage problems. For example, we can easily adapt the methods to solve problems such as:
- Finding a percentage of a number: What is 25% of 120?
- Finding the percentage one number is of another: What percentage of 50 is 10?
- Increasing or decreasing a number by a percentage: Increase 80 by 15%.
By mastering the fundamentals of percentage calculations, you equip yourself with valuable problem-solving skills applicable across a wide range of disciplines and situations.
Beyond the Numbers: The Importance of Mathematical Literacy
The ability to solve problems like "0.8 of what number is 6" is more than just about getting the right answer; it's about developing mathematical literacy. Mathematical literacy is the ability to understand and use mathematics effectively in various contexts. It equips individuals with the skills to analyze information, solve problems, and make informed decisions in their personal and professional lives.
Conclusion: Mastering Percentages for a Brighter Future
The simple question, "0.8 of what number is 6?", serves as a gateway to understanding the power of percentages and proportions. By mastering the various methods of solving this type of problem, from algebraic manipulation to using the percentage formula, you gain a valuable skillset applicable across numerous fields. This ability extends beyond mere calculation; it cultivates mathematical literacy, empowering you to navigate complex situations with confidence and make informed decisions in your daily life. Remember, the ability to understand and apply these mathematical concepts is a valuable asset in today's world. So, keep practicing, keep exploring, and keep expanding your mathematical horizons!
Latest Posts
Latest Posts
-
Which Of The Following Truly Resolves Inner Conflict
Jun 06, 2025
-
Task Analysis Steps May Be Used To Create Visual Schedules
Jun 06, 2025
-
What Is A Feature Of The Architects Scale
Jun 06, 2025
-
When You Have Properly Parked Your Vehicle
Jun 06, 2025
-
June Has A Credit Card Balance Of 4350
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about 0.8 Of What Number Is 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.