.001 Is 1/10 Of What Number
Breaking News Today
Jun 05, 2025 · 5 min read
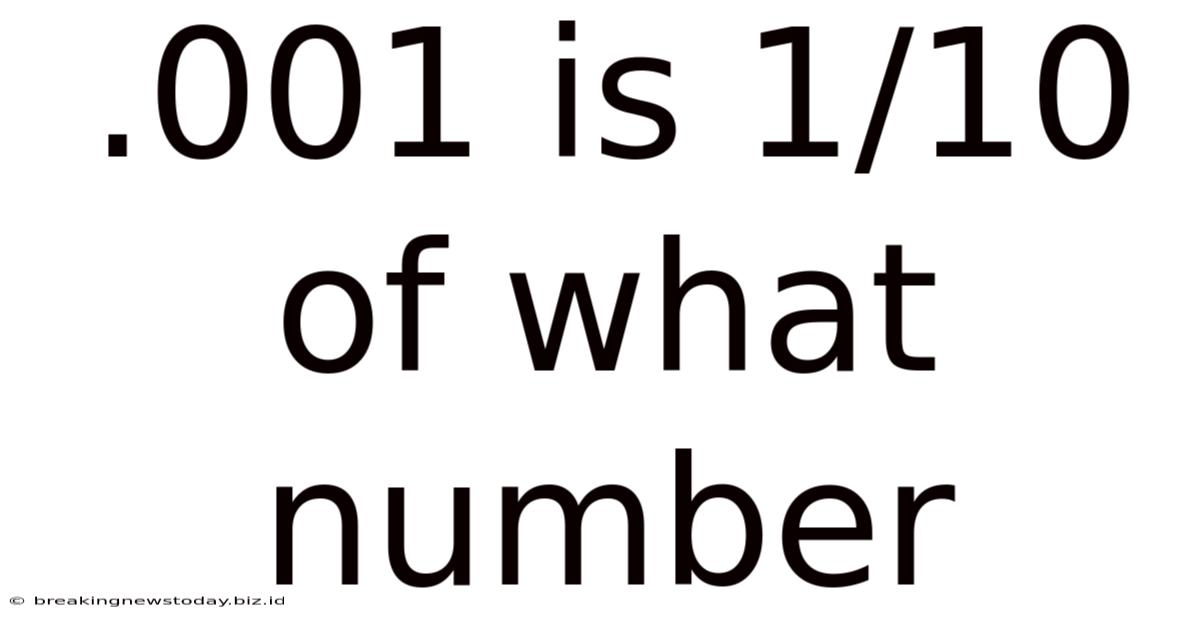
Table of Contents
.001 is 1/10 of What Number? Unlocking the World of Decimal Conversions
Understanding decimal conversions is fundamental to math, science, and various everyday applications. This article delves into the question, ".001 is 1/10 of what number?", exploring different methods to solve it and expanding on the broader concepts of decimal fractions and their practical uses. We'll also examine similar problems and explore how to approach them effectively, solidifying your understanding of decimal manipulation.
Understanding Decimals and Fractions
Before diving into the core problem, let's refresh our understanding of decimals and fractions. Decimals represent parts of a whole using a base-ten system, separated by a decimal point. For instance, 0.1 represents one-tenth (1/10), 0.01 represents one-hundredth (1/100), and 0.001 represents one-thousandth (1/1000). Fractions, on the other hand, express parts of a whole using a numerator (the top number) and a denominator (the bottom number). Both decimals and fractions are interchangeable, meaning you can convert one form into the other.
Converting Decimals to Fractions
Converting decimals to fractions is a straightforward process:
-
Identify the place value: Determine the place value of the last digit in the decimal. For 0.001, the last digit (1) is in the thousandths place.
-
Write the fraction: The last digit becomes the numerator, and the place value becomes the denominator. Therefore, 0.001 becomes 1/1000.
-
Simplify (if necessary): Sometimes, you can simplify the fraction by finding the greatest common divisor (GCD) of the numerator and denominator. In this case, 1/1000 is already in its simplest form.
Converting Fractions to Decimals
Conversely, converting fractions to decimals involves dividing the numerator by the denominator:
-
Perform the division: Divide the numerator by the denominator. For example, to convert 1/10 to a decimal, divide 1 by 10, resulting in 0.1.
-
Add a decimal point and zeros: If the division doesn't result in a whole number, add a decimal point and zeros to the numerator until you obtain a terminating or repeating decimal.
Solving the Problem: .001 is 1/10 of What Number?
Now, let's tackle the central question: ".001 is 1/10 of what number?" We can approach this problem using several methods:
Method 1: Using Fractions
-
Express .001 as a fraction: As discussed earlier, 0.001 is equal to 1/1000.
-
Set up an equation: Let 'x' represent the unknown number. The problem states that 1/1000 is 1/10 of x. This can be written as: (1/10) * x = 1/1000
-
Solve for x: To isolate x, multiply both sides of the equation by 10: x = (1/1000) * 10
-
Simplify: This simplifies to x = 1/100 or 0.01
Method 2: Using Decimals
-
Set up an equation: Again, let 'x' be the unknown number. The problem can be expressed as: 0.001 = (1/10) * x
-
Solve for x: Multiply both sides by 10: 0.001 * 10 = x
-
Simplify: This simplifies to x = 0.01
Method 3: Logical Reasoning
We know that 0.001 is one-thousandth. If 0.001 is one-tenth of a number, that number must be ten times larger. Therefore, we simply multiply 0.001 by 10, which gives us 0.01.
Expanding on Decimal Conversions: Real-World Applications
Understanding decimal conversions isn't just an academic exercise; it's crucial in various real-world scenarios:
-
Finance: Calculating interest rates, taxes, discounts, and currency conversions all involve decimal manipulation.
-
Science: Measurements in physics, chemistry, and other scientific fields often rely on decimals for precision.
-
Engineering: Designing and building structures requires precise calculations involving decimals.
-
Computer Science: Binary numbers, the foundation of computer programming, are inherently linked to decimal representation.
-
Everyday Life: We encounter decimals daily when dealing with money, weights, and measurements.
Similar Problems and Solving Strategies
Let's explore a few similar problems to reinforce your understanding:
Problem 1: 0.05 is 1/5 of what number?
Using the same methods as above, we can set up the equation: 0.05 = (1/5) * x. Multiplying both sides by 5, we get x = 0.25.
Problem 2: 1/200 is 1/10 of what number?
First, express 1/200 as a decimal (0.005). Then, set up the equation: 0.005 = (1/10) * x. Multiplying both sides by 10 gives x = 0.05.
Problem 3: 0.0001 is 1/100 of what number?
Here, the equation becomes 0.0001 = (1/100) * x. Multiplying both sides by 100, we get x = 0.01
Mastering Decimal Conversions: Tips and Tricks
-
Practice Regularly: The more you practice converting decimals and fractions, the more comfortable you'll become.
-
Visual Aids: Using diagrams or visual aids can help you grasp the concept of decimal place values.
-
Utilize Online Resources: Numerous online calculators and tutorials can assist with decimal conversions.
-
Break Down Complex Problems: Tackle complex problems by breaking them down into smaller, more manageable steps.
-
Check Your Work: Always double-check your answers to ensure accuracy.
Conclusion: The Power of Understanding Decimals
The seemingly simple question, ".001 is 1/10 of what number?", opens a door to a wider understanding of decimal conversions and their far-reaching applications. By mastering these conversions, you equip yourself with essential mathematical skills applicable across various fields, enhancing your problem-solving abilities and boosting your confidence in tackling numerical challenges. Remember to practice regularly and utilize the diverse strategies discussed to solidify your understanding and become proficient in the world of decimals.
Latest Posts
Latest Posts
-
5 11 Unit Test The Power Of Language
Jun 06, 2025
-
Which Sentences Contain Phrases That Are Hyphenated Correctly
Jun 06, 2025
-
El Tiempo Is Corto Means That Bolsa And Sancho
Jun 06, 2025
-
Which Phrase Connects These Characters To The Southern Gothic Genre
Jun 06, 2025
-
Risk And Compliance Culture At Usaa Is Characterized By
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about .001 Is 1/10 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.