.002 Is 1/100 Of What Decimal
Breaking News Today
Jun 06, 2025 · 5 min read
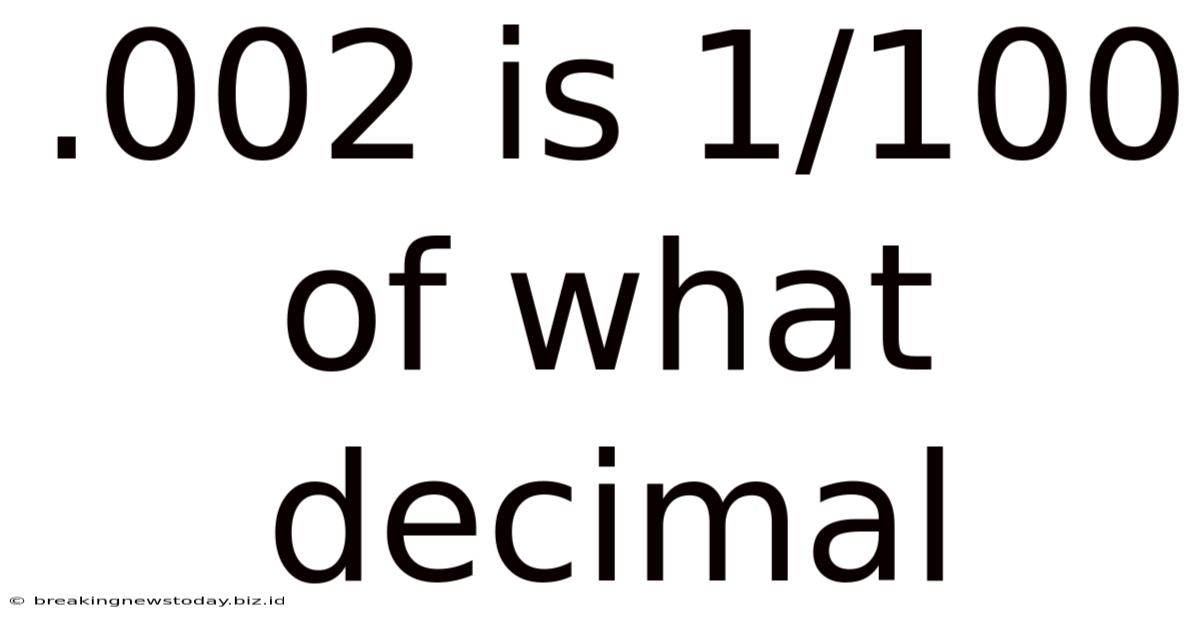
Table of Contents
.002 is 1/100th of What Decimal? Unraveling Decimal Relationships
This seemingly simple question, ".002 is 1/100th of what decimal?", delves into the fascinating world of decimal representation and fractional equivalents. Understanding the relationship between decimals and fractions is crucial in various fields, from mathematics and science to finance and computer programming. This article will not only answer the core question but also explore the underlying principles, providing you with a comprehensive understanding of decimal manipulation and its practical applications.
Understanding Decimals and Fractions
Before diving into the problem, let's refresh our understanding of decimals and fractions. Decimals are a way of representing numbers that are not whole numbers. They use a base-ten system, where each digit to the right of the decimal point represents a power of ten. For instance:
- 0.1 represents one-tenth (1/10)
- 0.01 represents one-hundredth (1/100)
- 0.001 represents one-thousandth (1/1000)
Fractions, on the other hand, represent parts of a whole. They are expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). The denominator indicates the number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
The key to solving our problem lies in the ability to convert between decimals and fractions seamlessly.
Solving the Problem: .002 is 1/100th of What Decimal?
The question states that 0.002 is one-hundredth (1/100) of an unknown decimal. We can express this relationship mathematically as:
0.002 = (1/100) * x where 'x' is the unknown decimal.
To solve for 'x', we need to isolate it. We can do this by multiplying both sides of the equation by 100:
100 * 0.002 = 100 * (1/100) * x
This simplifies to:
0.2 = x
Therefore, 0.002 is 1/100th of 0.2.
Alternative Approach: Using Fraction Conversion
We can also solve this problem by first converting the decimal 0.002 into a fraction:
0.002 = 2/1000
Now, we can rewrite the problem as:
2/1000 = (1/100) * x
To solve for x, we can multiply both sides by 100:
(2/1000) * 100 = x
This simplifies to:
2/10 = x
And further simplified:
x = 1/5
Finally, converting the fraction 1/5 back to a decimal gives us:
x = 0.2
This confirms our previous result: 0.002 is 1/100th of 0.2.
Practical Applications and Real-World Examples
Understanding decimal relationships is vital in numerous real-world scenarios. Here are a few examples:
- Finance: Calculating interest rates, discounts, and tax percentages often involves manipulating decimals and fractions. For instance, understanding that 0.05 represents 5% is crucial for calculating interest earned or taxes owed.
- Science: Measurements in scientific experiments often involve decimals, especially in fields like physics and chemistry where precision is paramount. Converting between decimal and fractional representations helps in simplifying calculations and expressing results accurately.
- Engineering: Engineering designs rely heavily on precise calculations, and a solid grasp of decimals is essential for ensuring accuracy in measurements and calculations.
- Computer Programming: Computer programming frequently uses decimal representations for various data types, such as floating-point numbers. Understanding decimal relationships is vital for writing efficient and accurate code.
Expanding Your Understanding: More Complex Decimal Relationships
Let's expand on this concept and explore more complex scenarios involving decimal relationships. Consider these examples:
Example 1: 0.005 is what fraction of 0.5?
First, convert both decimals to fractions:
0.005 = 5/1000 0.5 = 5/10
Now, express the relationship as a fraction:
(5/1000) / (5/10) = (5/1000) * (10/5) = 1/100
Therefore, 0.005 is 1/100th of 0.5.
Example 2: What decimal is 1/200th of 0.08?
First, convert 1/200 to a decimal:
1/200 = 0.005
Now, multiply this decimal by 0.08:
0.005 * 0.08 = 0.0004
Therefore, 0.0004 is 1/200th of 0.08.
These examples highlight how manipulating decimals and fractions allows us to solve various problems efficiently.
Mastering Decimal and Fraction Conversions: Tips and Techniques
To confidently tackle problems involving decimals and fractions, mastering conversion techniques is crucial. Here are some key tips:
- Understanding Place Value: A strong understanding of place value in decimals is fundamental. Each digit to the right of the decimal point represents a decreasing power of 10.
- Converting Decimals to Fractions: To convert a decimal to a fraction, write the decimal as a fraction with the denominator as a power of 10 (10, 100, 1000, etc., depending on the number of decimal places). Then, simplify the fraction if possible.
- Converting Fractions to Decimals: To convert a fraction to a decimal, divide the numerator by the denominator. You can perform long division or use a calculator.
- Practicing Regularly: Regular practice is key to solidifying your understanding and improving your proficiency. Start with simple problems and gradually progress to more complex ones.
Conclusion: The Power of Understanding Decimal Relationships
The seemingly straightforward question, ".002 is 1/100th of what decimal?", unveils a world of intricate relationships between decimals and fractions. Understanding these relationships is not just about solving mathematical problems; it's about gaining a foundational skill applicable across numerous disciplines. By mastering decimal and fraction conversions and practicing regularly, you can confidently tackle complex calculations and applications, ultimately enhancing your problem-solving abilities and contributing to success in various fields. Remember to approach these problems methodically, breaking them down into smaller, manageable steps, and utilizing the various techniques described above to achieve accurate and efficient solutions. The more you practice, the more intuitive these conversions become, transforming what might initially seem challenging into a straightforward process.
Latest Posts
Latest Posts
-
Parsons And Her Colleagues Are Doing A Study
Jun 07, 2025
-
Which Phrase Describes How Jupiter And Saturn Are Similar
Jun 07, 2025
-
Good Housekeeping Practices For Ammunition Storage
Jun 07, 2025
-
Carson Needs 3 Quarts Of Water
Jun 07, 2025
-
Compare The Two Interview Subjects Views On The Great Depression
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about .002 Is 1/100 Of What Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.