1 2/3 Of The Number Is 4.75
Breaking News Today
Jun 07, 2025 · 5 min read
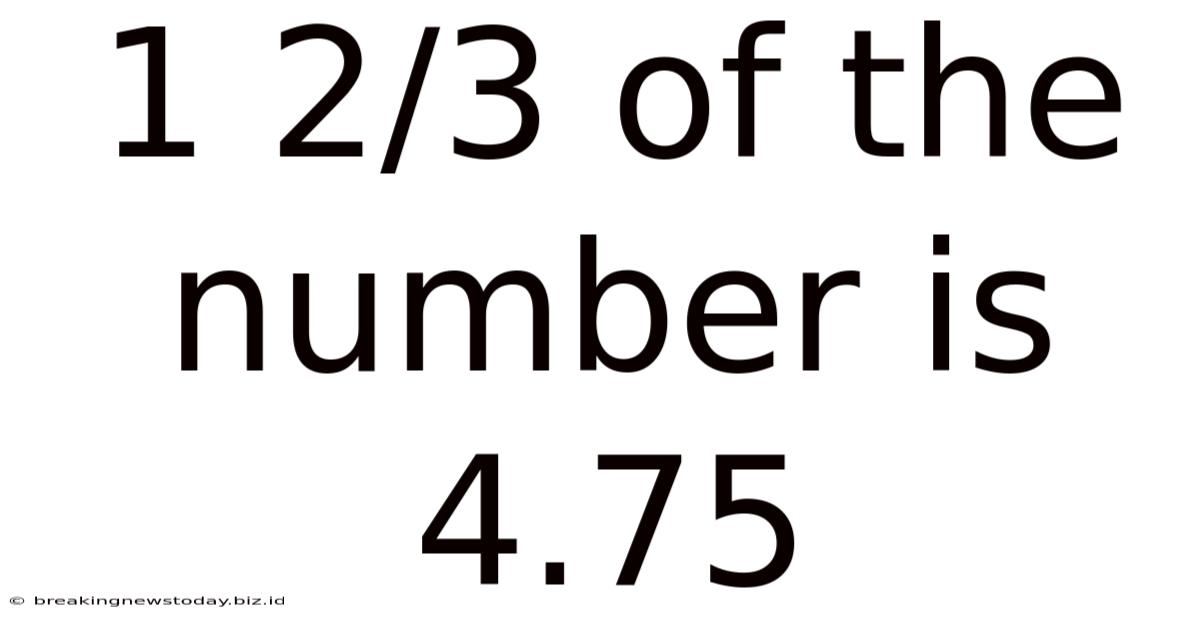
Table of Contents
1 2/3 of a Number is 4.75: Unraveling the Mathematical Mystery
This seemingly simple mathematical problem – "1 2/3 of a number is 4.75" – presents a fantastic opportunity to explore several key mathematical concepts and problem-solving strategies. While the solution itself is straightforward, the process of arriving at the answer provides valuable insights into fractions, decimals, equations, and algebraic reasoning. This article will delve into the solution, explain the underlying principles, and offer various approaches to tackling similar problems.
Understanding the Problem: Deconstructing the Phrase
Before we jump into the solution, let's break down the problem statement: "1 2/3 of a number is 4.75." This phrase can be translated into a mathematical equation. The key is to understand the meaning of "of" in this context. "Of" signifies multiplication. Therefore, the problem can be rewritten as:
(1 2/3) * x = 4.75
Where 'x' represents the unknown number we are trying to find.
Method 1: Solving using Fractions
This method utilizes the power of fractions and their inherent properties. First, we convert the mixed number 1 2/3 into an improper fraction:
1 2/3 = (3*1 + 2)/3 = 5/3
Now, our equation becomes:
(5/3) * x = 4.75
To isolate 'x', we need to multiply both sides of the equation by the reciprocal of 5/3, which is 3/5:
(3/5) * (5/3) * x = 4.75 * (3/5)
This simplifies to:
x = 4.75 * (3/5)
Now, we can perform the multiplication. It's often easier to convert the decimal 4.75 into a fraction:
4.75 = 4 and 75/100 = 4 and 3/4 = (4*4 + 3)/4 = 19/4
Substituting this back into our equation:
x = (19/4) * (3/5)
Multiplying the numerators and denominators:
x = 57/20
Finally, we convert this improper fraction back into a decimal or mixed number:
x = 2.85 or x = 2 and 17/20
Method 2: Solving using Decimals
This approach leverages the flexibility of decimals. We begin by converting the mixed number 1 2/3 into a decimal:
1 2/3 = 1 + (2/3) ≈ 1 + 0.6667 ≈ 1.6667
Note: We use an approximation here due to the repeating decimal nature of 2/3. The more decimal places we use, the more accurate our final answer will be. For simplicity, we'll use 1.6667.
Now our equation is:
1.6667 * x = 4.75
To solve for x, we divide both sides of the equation by 1.6667:
x = 4.75 / 1.6667
Performing the division:
x ≈ 2.85
Again, we obtain an approximate value due to the use of an approximate decimal value for 1 2/3. The slight discrepancy between the results from this method and Method 1 is due to the rounding of the decimal representation of 2/3.
Method 3: Solving using Algebra and Proportions
This method offers a different perspective by framing the problem as a proportion. We can express the problem as:
(5/3) / 4.75 = 1 / x
This proportion states that the ratio of 5/3 to 4.75 is equal to the ratio of 1 to the unknown number x. Cross-multiplying gives us:
(5/3) * x = 4.75
This equation is identical to the one we obtained in Method 1. Solving this as before:
x = 4.75 * (3/5) = (19/4) * (3/5) = 57/20 = 2.85
Verification and Accuracy
To verify our solution, we can substitute x = 2.85 back into the original equation:
(1 2/3) * 2.85 = 4.75
(5/3) * 2.85 = 4.75
4.75 = 4.75
The equation holds true, confirming our solution.
Expanding the Concept: Similar Problems and Applications
The problem "1 2/3 of a number is 4.75" serves as a foundational example for solving various percentage, fraction, and decimal problems. This methodology can be extended to a broad range of real-world applications. For example:
Percentage Problems:
Let's say you know that 15% of a certain amount is $75. This can be set up as an equation and solved similarly to our initial problem:
0.15 * x = 75
x = 75 / 0.15 = 500
This indicates that the original amount was $500.
Fraction Problems involving Ratios:
If two-fifths of a quantity equals 12, the solution method would mirror the steps used above:
(2/5) * x = 12
x = 12 * (5/2) = 30
Real-world Applications:
This fundamental mathematical skill is crucial in numerous real-world situations including:
- Baking and Cooking: Adjusting recipes based on ingredient availability requires these calculations.
- Finance: Calculating discounts, interest, or tax amounts requires a clear understanding of percentages and fractions.
- Construction: Determining material quantities for projects involving scaling blueprints or plans involves similar calculations.
- Data Analysis: Analyzing proportions and percentages within datasets hinges on this foundational understanding.
Conclusion: Mastering Mathematical Problem Solving
Solving the problem "1 2/3 of a number is 4.75" is more than just finding a numerical answer; it's about understanding the underlying mathematical principles and developing problem-solving skills. By employing different methods, we've demonstrated the flexibility and interconnectedness of various mathematical concepts. This knowledge is not just academically valuable, but also incredibly useful in tackling everyday challenges that require mathematical reasoning and calculation. The ability to effectively work with fractions, decimals, percentages, and equations is a highly transferable skill that empowers individuals to confidently approach and solve a wide variety of problems in both academic and real-world settings. The key takeaway is not just the answer (2.85), but the process of arriving at it – a process that builds mathematical fluency and confidence. Remember to always check your work to ensure accuracy and deepen your understanding of the problem's solution.
Latest Posts
Latest Posts
-
The First Step In Preventing Disturbances Is To Create A
Jun 07, 2025
-
Factory Production Of The Nineteenth Century Piano Meant
Jun 07, 2025
-
What Is F 5 8 1 1 8
Jun 07, 2025
-
A Grocery Store Receives Deliveries Of Corn
Jun 07, 2025
-
Which Name Accurately Describes The Figure Shown Below And Why
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 1 2/3 Of The Number Is 4.75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.