12 Is What Percent Of 144
Breaking News Today
Jun 06, 2025 · 5 min read
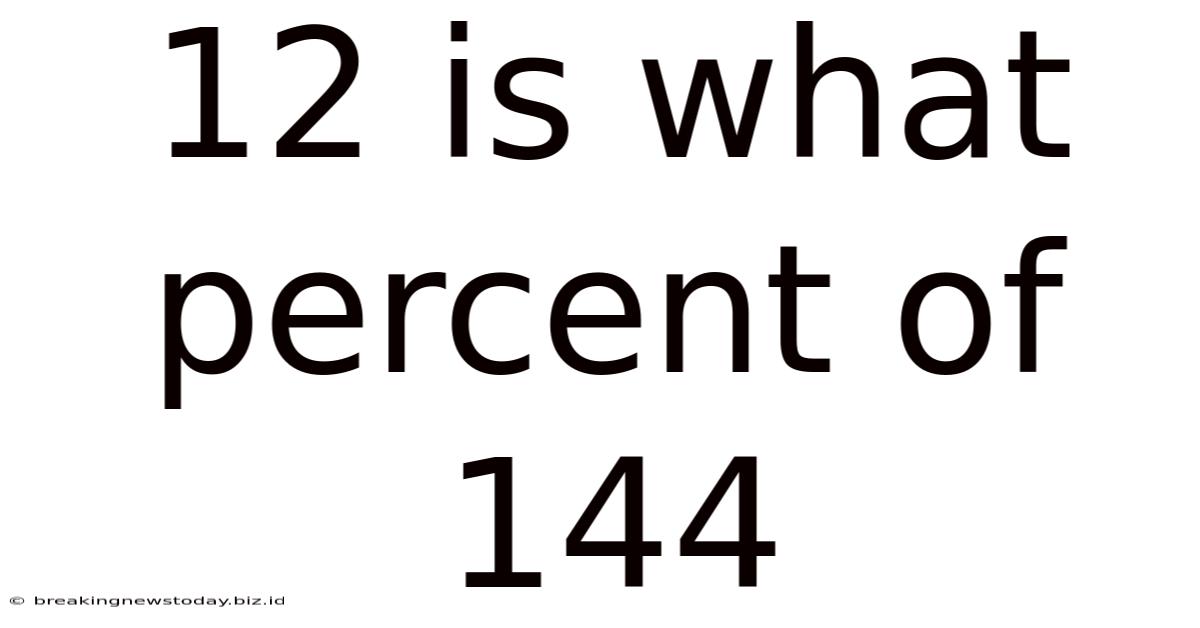
Table of Contents
12 is What Percent of 144? A Deep Dive into Percentage Calculations
This seemingly simple question, "12 is what percent of 144?", opens the door to a fascinating exploration of percentages, their applications, and the underlying mathematical principles. While the answer itself is straightforward, understanding the why and how behind the calculation is crucial for anyone seeking to master this fundamental concept in mathematics and its widespread real-world applications. This comprehensive guide will not only provide the solution but also delve into the various methods for solving percentage problems, offering practical examples and demonstrating how to apply this knowledge effectively.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The term "percent" itself derives from the Latin "per centum," meaning "out of one hundred." Therefore, any percentage can be represented as a fraction with a denominator of 100 or as a decimal. For example, 25% can be written as 25/100, 0.25, or even 1/4 (since 25/100 simplifies to 1/4). This interchangeable representation is a key to solving percentage problems efficiently.
Method 1: The Proportion Method
This method relies on setting up a proportion – two equivalent ratios – to solve for the unknown percentage. We can represent the problem as:
12/144 = x/100
Where:
- 12 represents the part.
- 144 represents the whole.
- x represents the unknown percentage we're trying to find.
- 100 represents the total percentage (100%).
To solve for x, we cross-multiply:
12 * 100 = 144 * x
1200 = 144x
x = 1200 / 144
x = 8.333...%
Therefore, 12 is approximately 8.33% of 144. The recurring decimal indicates that the percentage is not a whole number. This is perfectly acceptable and often the case in percentage calculations.
Method 2: The Decimal Method
This method involves converting the fraction into a decimal and then multiplying by 100 to express it as a percentage.
First, represent the problem as a fraction:
12/144
Now, simplify the fraction (if possible):
12/144 simplifies to 1/12
Next, divide the numerator by the denominator to convert it into a decimal:
1 ÷ 12 ≈ 0.08333...
Finally, multiply the decimal by 100 to obtain the percentage:
0.08333... * 100 ≈ 8.333...%
This method provides the same result as the proportion method, confirming the accuracy of our calculations.
Method 3: Using a Calculator
Modern calculators have built-in percentage functions, making the calculation even more straightforward. Simply enter the following:
(12 ÷ 144) * 100
The calculator will directly display the answer as approximately 8.333...%. This is the most efficient method for quick calculations.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-world situations:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For example, determining the amount of interest earned on a savings account or the discount applied to a sale item.
-
Business: Analyzing sales figures, market share, growth rates, and cost percentages are essential for business decision-making. For example, calculating the percentage increase or decrease in sales compared to previous periods.
-
Science: Representing experimental results, statistical data, and error margins often uses percentages to convey the relative magnitude of measurements.
-
Everyday Life: Calculating tips in restaurants, determining sale prices, understanding nutritional information on food labels, and even interpreting weather forecasts all involve percentage calculations.
Extending the Concept: Variations on the Theme
Let's explore some variations of the core problem to further solidify our understanding:
-
Finding the Whole: If we knew that 12 represents 8.33% of a number, how would we find that number? We'd use the formula: Whole = (Part / Percentage) * 100. In this case, Whole = (12 / 8.33%) * 100 ≈ 144.
-
Finding the Part: If we knew that 15% of a number is 18, how would we find the number? We’d use the formula: Part = (Percentage/100) * Whole. Therefore, Whole = 18/ (15/100) = 120
-
Percentage Change: Calculating percentage increase or decrease involves finding the difference between two values, dividing by the original value, and multiplying by 100. For example, if a price increases from $100 to $120, the percentage increase is ((120 - 100) / 100) * 100 = 20%.
Mastering Percentages: Tips and Tricks
-
Practice Regularly: The more you practice, the more comfortable and efficient you'll become at solving percentage problems.
-
Understand the Fundamentals: A strong grasp of fractions and decimals is essential for mastering percentages.
-
Use Multiple Methods: Trying different methods helps reinforce your understanding and allows you to choose the most efficient approach for each problem.
-
Utilize Online Resources: Numerous online calculators and tutorials can help you practice and check your answers.
-
Apply to Real-World Scenarios: Try applying percentage calculations to your daily life – this will solidify your understanding and demonstrate the practicality of the concept.
Conclusion: The Significance of Percentage Calculations
The seemingly simple question, "12 is what percent of 144?" has led us on a journey through the world of percentages. We’ve discovered multiple methods for solving this type of problem, explored various applications, and discussed strategies for mastering this fundamental mathematical concept. Understanding percentages is not just a matter of passing a math test; it's a vital skill that empowers individuals to navigate the complexities of finance, business, science, and everyday life with greater confidence and competence. The ability to calculate percentages efficiently and accurately is a cornerstone of numerical literacy and a valuable asset in any field. By consistently practicing and applying these principles, you can transform your understanding of percentages from a simple calculation to a powerful tool for problem-solving and decision-making.
Latest Posts
Latest Posts
-
A Voltage Tester Gives Only Approximate Voltage Measurements
Jun 07, 2025
-
This Excerpt Best Shows That The Ancient Greeks Valued
Jun 07, 2025
-
According To Your Textbook Effective Listening Skills Are Important For
Jun 07, 2025
-
Aggregate Is A Form Of Plagiarism That Happens When
Jun 07, 2025
-
Pandora Loves Attention And Likes To Learn
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 12 Is What Percent Of 144 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.