120 Of X Is Equal To 78
Breaking News Today
Jun 01, 2025 · 5 min read
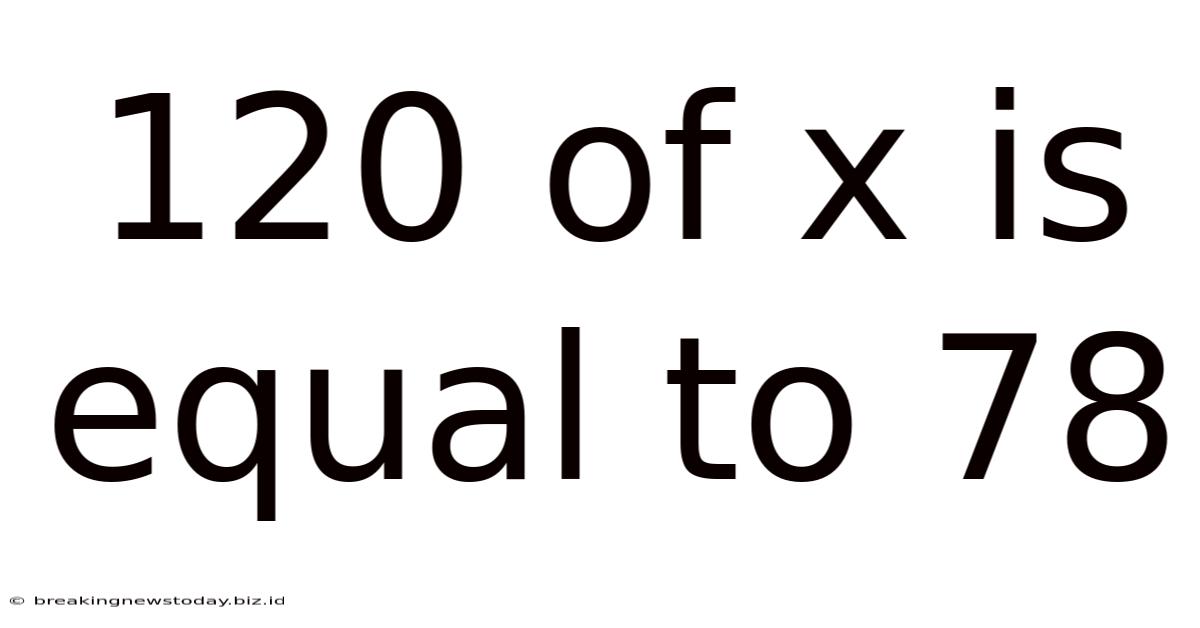
Table of Contents
120% of X is Equal to 78: A Comprehensive Guide to Percentage Calculations
This article delves into the intricacies of percentage calculations, using the example "120% of X is equal to 78" as a springboard to explore various methods of solving such problems and their broader applications. We will unpack the fundamental concepts, demonstrate multiple solution approaches, and explore the practical relevance of percentage calculations in diverse fields. This comprehensive guide is designed to enhance your understanding of percentages and equip you with the skills to tackle similar problems effectively.
Understanding the Problem: 120% of X = 78
The statement "120% of X is equal to 78" presents a simple yet fundamental percentage problem. It essentially asks: what is the value of X when 120% of it equals 78? This problem showcases a scenario where a quantity (X) is increased by 20% of its original value, resulting in a final value of 78. Understanding this core concept is vital for solving the problem and applying similar percentage calculations in various real-world contexts.
Method 1: Algebraic Approach
This method utilizes basic algebra to solve for X. We can translate the statement "120% of X is equal to 78" into an algebraic equation:
-
Convert the percentage to a decimal: 120% is equivalent to 1.2 (120/100 = 1.2)
-
Formulate the equation: 1.2X = 78
-
Solve for X: Divide both sides of the equation by 1.2:
X = 78 / 1.2 = 65
Therefore, the value of X is 65.
Verifying the Solution
To verify our solution, let's substitute X = 65 back into the original equation:
1.2 * 65 = 78
The equation holds true, confirming that our solution, X = 65, is correct.
Method 2: Unitary Method
The unitary method is a straightforward approach focusing on finding the value of 1% of X first and then scaling it up to find the value of 100% (or X).
-
Find 1% of X: If 120% of X is 78, then 1% of X is 78/120 = 0.65
-
Find 100% of X (X): Since 1% of X is 0.65, 100% of X (which is X) will be 0.65 * 100 = 65
Therefore, the value of X is 65. This method provides a step-by-step approach that can be particularly helpful for those less familiar with algebraic manipulation.
Method 3: Using Proportions
This method utilizes the concept of ratios and proportions to solve for X. We can set up a proportion:
120/100 = 78/X
Cross-multiplying gives:
120X = 7800
Solving for X:
X = 7800/120 = 65
Thus, the value of X is 65. This method demonstrates the equivalence between percentages and ratios, providing an alternative perspective on solving percentage problems.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial across numerous disciplines and everyday scenarios. Here are some examples:
1. Business and Finance:
-
Profit and Loss Calculations: Determining profit margins, calculating discounts, analyzing financial statements, and assessing investment returns all involve percentage calculations. For example, a company might want to know what their initial investment (X) was if their 120% return (after including the investment) was $78,000.
-
Interest Rates: Calculating simple interest, compound interest, and analyzing loan repayments require a thorough understanding of percentages.
-
Tax Calculations: Determining sales tax, income tax, and other taxes often involves percentage calculations based on income or expenditure.
2. Science and Engineering:
-
Data Analysis: Percentages are frequently used to represent data proportions, making it easier to interpret results and draw conclusions from scientific experiments or statistical surveys.
-
Chemical Concentrations: Calculating the concentration of solutions, such as molarity or percentage by weight, relies heavily on percentage calculations.
-
Engineering Design: Percentages are utilized in design calculations, stress analysis, and material selection to ensure safety and efficiency.
3. Everyday Life:
-
Shopping Discounts: Calculating the final price of discounted items, often advertised as percentage discounts (e.g., 20% off), requires applying percentage calculations.
-
Tip Calculation: Determining the appropriate tip amount in restaurants usually involves calculating a certain percentage of the bill.
-
Grade Calculations: Many educational systems use percentages to represent grades and overall academic performance. A student might calculate what their original score (X) needs to be to have a final score of 78 after being penalized (or increased) by a certain percentage.
Expanding the Concept: Beyond 120%
The core principle behind solving "120% of X = 78" can be extended to other percentage problems. The process of converting percentages to decimals and formulating algebraic equations remains consistent. For instance:
-
Solving for a percentage increase: If X increases by 25% to become 75, what is the value of X? (1.25X = 75)
-
Solving for a percentage decrease: If X decreases by 15% to become 68, what is the value of X? (0.85X = 68)
-
Solving for the original value after a percentage change: If X undergoes a 30% increase and the new value is 91, find the original value of X. (1.3X = 91)
Mastering the techniques outlined in this article—algebraic approach, unitary method, and proportion—will provide you with the tools to tackle any percentage problem efficiently and accurately.
Conclusion
The seemingly simple problem, "120% of X is equal to 78," serves as an excellent illustration of the fundamental importance of percentage calculations in various aspects of life. Understanding the different methods for solving such problems, from algebraic manipulation to the use of proportions, empowers you to handle more complex percentage-related calculations with confidence. The practical applications extend beyond academic exercises, impacting various fields, from finance and business to science and everyday life. By grasping these concepts, you enhance your analytical skills and gain a valuable tool for navigating numerous real-world scenarios. Remember to always verify your answers to ensure accuracy and build a solid foundation in percentage calculations.
Latest Posts
Latest Posts
-
Bolsa Feels Bad For Sanchos Loss True False
Jun 02, 2025
-
Which Of The Following Best Describes Nacas Membership Dues
Jun 02, 2025
-
When Evacuating Victims And Endangered Personnel In A Severe Emergency
Jun 02, 2025
-
An Ultrasound Tech Is Trying To Identify An Object
Jun 02, 2025
-
Do Mobile And Desktop Devices Pose The Same Security Risks
Jun 02, 2025
Related Post
Thank you for visiting our website which covers about 120 Of X Is Equal To 78 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.