14.2 Is 35.5 Of What Number
Breaking News Today
Jun 06, 2025 · 4 min read
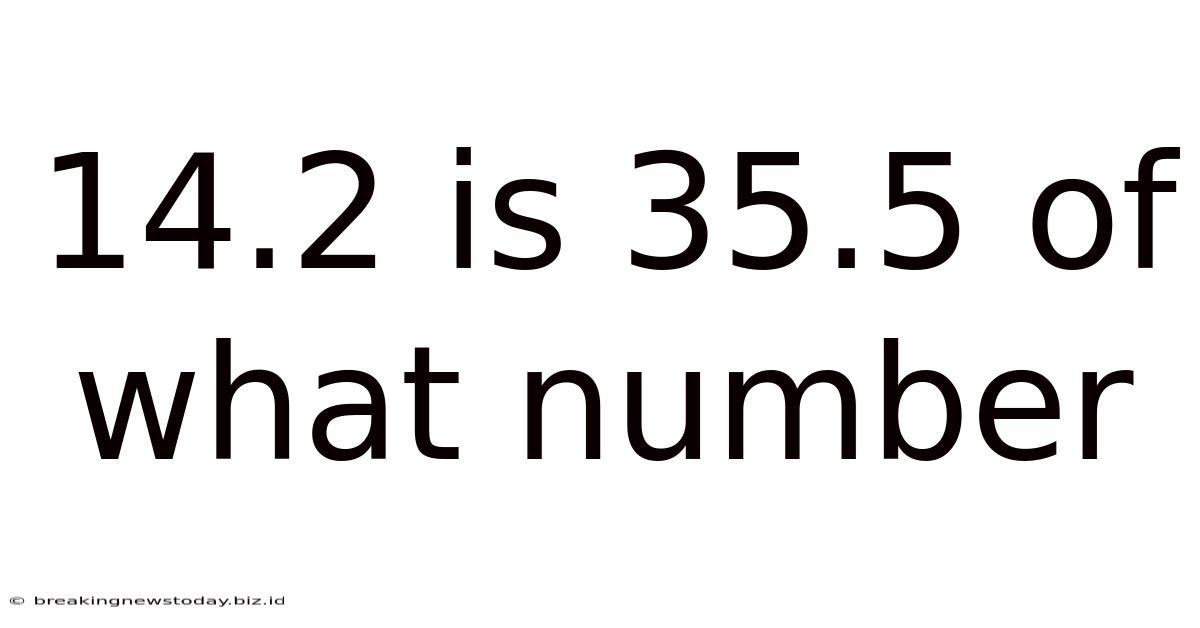
Table of Contents
14.2 is 35.5% of What Number? Unraveling Percentage Problems
This seemingly simple question, "14.2 is 35.5% of what number?", opens the door to a deeper understanding of percentages and their applications in various fields. While the immediate solution might involve a quick calculation, let's delve into the underlying concepts, explore different solution methods, and uncover the practical relevance of percentage problems.
Understanding Percentages: The Foundation
Percentages are a fundamental aspect of mathematics, representing fractions with a denominator of 100. They're used extensively in everyday life, from calculating discounts and taxes to understanding statistics and financial reports. The key to solving percentage problems lies in translating the worded problem into a mathematical equation.
Deconstructing the Problem
The statement "14.2 is 35.5% of what number?" can be broken down as follows:
- 14.2: This is the resulting value or part of the whole.
- 35.5%: This is the percentage representing the ratio of the part to the whole.
- What number?: This is the unknown value, the whole we are trying to find.
Methods for Solving Percentage Problems
Several methods can be used to solve this type of problem. Let's explore three common approaches:
Method 1: Using the Percentage Formula
The most straightforward approach uses the basic percentage formula:
Part = Percentage × Whole
In our problem:
- Part = 14.2
- Percentage = 35.5% = 0.355 (Remember to convert the percentage to a decimal by dividing by 100)
- Whole = x (the unknown value)
Substituting these values into the formula, we get:
14.2 = 0.355x
To solve for x, divide both sides of the equation by 0.355:
x = 14.2 / 0.355
x ≈ 39.999... ≈ 40
Therefore, 14.2 is approximately 35.5% of 40.
Method 2: Using Proportions
Another effective method involves setting up a proportion:
Part / Whole = Percentage / 100
In our case:
14.2 / x = 35.5 / 100
Cross-multiply to solve for x:
14.2 * 100 = 35.5x
1420 = 35.5x
x = 1420 / 35.5
x ≈ 40
Again, we arrive at the same solution: 40.
Method 3: Using the "Is/Of" Method
This method is particularly helpful for visualizing the problem. The "is" represents the part, the "of" represents the whole, and the percentage is the ratio. The equation becomes:
"Is" / "Of" = Percentage / 100
Substituting our values:
14.2 / x = 35.5 / 100
This leads to the same solution as Method 2, resulting in x ≈ 40.
Practical Applications of Percentage Problems
The ability to solve percentage problems is crucial in a wide array of situations:
Finance and Budgeting:
- Calculating interest: Determining the principal amount based on interest earned.
- Analyzing financial statements: Understanding profit margins, growth rates, and expense ratios.
- Managing personal finances: Tracking savings, investments, and debt.
Business and Sales:
- Calculating discounts and markups: Determining sale prices, profit margins, and pricing strategies.
- Analyzing sales data: Identifying trends, measuring performance, and making informed business decisions.
- Commission calculations: Calculating earnings based on sales performance.
Science and Research:
- Analyzing experimental data: Expressing results as percentages for clarity and comparison.
- Statistical analysis: Calculating percentages for various statistical measures.
- Presenting research findings: Communicating results using percentages to facilitate understanding.
Everyday Life:
- Calculating tips: Determining appropriate tips in restaurants and other service industries.
- Understanding sales tax: Calculating the final price of goods and services.
- Interpreting survey results: Analyzing data presented as percentages in polls and surveys.
Expanding on Percentage Calculations: Dealing with Complex Scenarios
While the problem "14.2 is 35.5% of what number?" provides a basic framework, real-world scenarios often involve more complex calculations. Let's consider some variations:
Scenario 1: Finding the Percentage Increase or Decrease
Suppose a product's price increased from $30 to $45. To find the percentage increase, follow these steps:
- Calculate the difference: $45 - $30 = $15
- Divide the difference by the original value: $15 / $30 = 0.5
- Multiply by 100 to express as a percentage: 0.5 * 100 = 50%
The price increased by 50%.
Scenario 2: Calculating Percentage Change with Multiple Increases/Decreases
If a value experiences multiple percentage changes, you cannot simply add or subtract the percentages. Instead, you must calculate each change sequentially. For example, if a value increases by 10% and then decreases by 10%, the final value will not be the same as the original.
Scenario 3: Compound Interest
Compound interest calculations involve repeated percentage increases over time. These calculations use the compound interest formula:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Conclusion: Mastering Percentages for Real-World Success
Understanding percentages and mastering their application is a valuable skill with widespread practical use. Whether you're managing personal finances, analyzing business data, or interpreting scientific results, the ability to solve percentage problems effectively is essential. By understanding the fundamental concepts and exploring various solution methods, you can confidently tackle a wide range of percentage-related challenges and make informed decisions in various aspects of life. Remember that practice is key to mastering this crucial mathematical skill. Continue to work through different problems, and soon you'll find yourself effortlessly solving even the most complex percentage calculations.
Latest Posts
Latest Posts
-
Which Health Reason Is Best For Learning About Advertising Techniques
Jun 07, 2025
-
Which Accurately Explains Concave And Convex Lenses
Jun 07, 2025
-
Which Statement Describes What This Graph Indicates About Government Spending
Jun 07, 2025
-
Find The Class Midpoint Of The Fico Score Interval 550 599
Jun 07, 2025
-
Which Of The Following Shows A Characteristic Of Pigmented Gels
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 14.2 Is 35.5 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.