18/10 More Than A Number X Is Equal To 29/5
Breaking News Today
Jun 04, 2025 · 4 min read
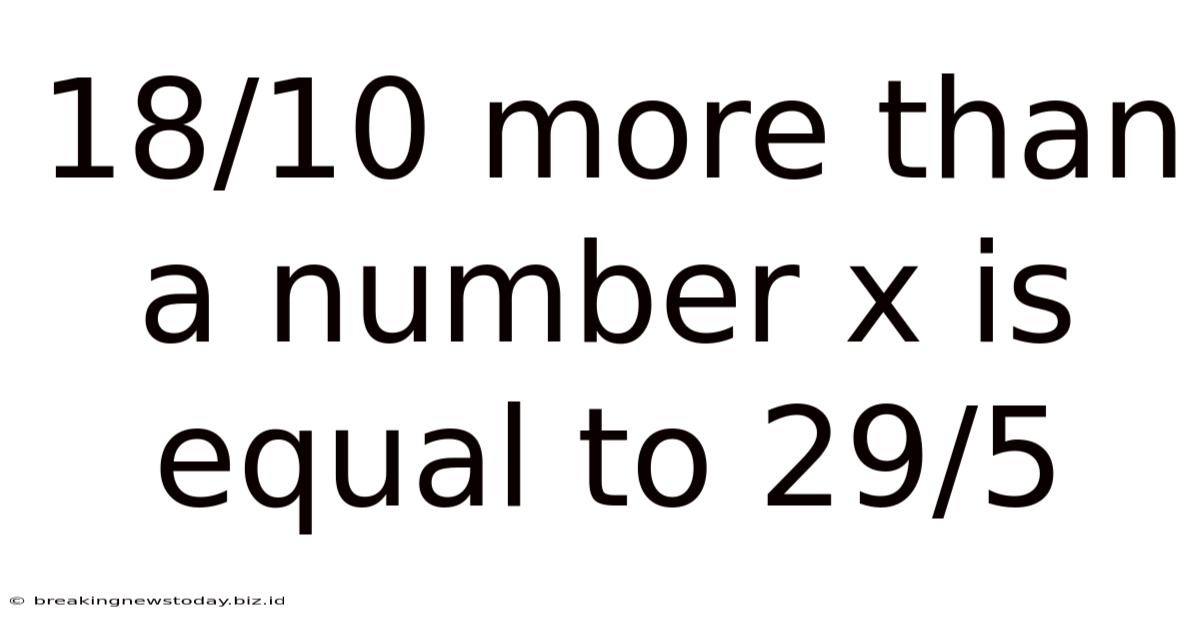
Table of Contents
18/10 More Than a Number x is Equal to 29/5: A Comprehensive Guide to Solving Algebraic Equations
This article delves into the solution of the algebraic equation "18/10 more than a number x is equal to 29/5," providing a step-by-step guide, exploring related concepts, and offering practical applications. We'll not only solve this specific equation but also equip you with the understanding to tackle similar problems confidently.
Understanding the Problem
The problem statement, "18/10 more than a number x is equal to 29/5," can be translated into a mathematical equation:
x + 18/10 = 29/5
This equation represents a fundamental algebraic concept: finding an unknown value (x) based on a given relationship. The core skill here is manipulating the equation to isolate 'x' on one side of the equals sign.
Step-by-Step Solution
Solving this equation involves several key steps:
1. Simplify Fractions
Before proceeding, it's crucial to simplify the fractions to make calculations easier. 18/10 can be simplified by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 2:
18/10 = 9/5
Our equation now becomes:
x + 9/5 = 29/5
2. Isolate the Variable (x)
Our goal is to get 'x' by itself. To achieve this, we need to subtract 9/5 from both sides of the equation. This maintains the balance of the equation:
x + 9/5 - 9/5 = 29/5 - 9/5
This simplifies to:
x = 20/5
3. Simplify the Result
Finally, simplify the fraction 20/5 by dividing both numerator and denominator by their GCD, which is 5:
20/5 = 4
Therefore, the solution to the equation is:
x = 4
Verification
To verify our solution, substitute the value of x (4) back into the original equation:
4 + 18/10 = 29/5
Simplifying the fractions:
4 + 9/5 = 29/5
Converting 4 to a fraction with a denominator of 5:
20/5 + 9/5 = 29/5
Adding the fractions:
29/5 = 29/5
Since both sides are equal, our solution (x = 4) is correct.
Expanding the Concept: Working with More Complex Equations
While this specific problem was relatively straightforward, let's explore how to approach more complex variations.
Equations with Multiple Variables
Imagine a slightly modified problem: "18/10 more than a number x is equal to 29/5 less than a number y." This translates to:
x + 18/10 = y - 29/5
Solving this requires additional information. You would need another equation relating x and y to find the values of both variables. This often involves systems of equations, which are solved using methods like substitution or elimination.
Equations with Parentheses and Other Operations
Consider an equation like:
3(x + 18/10) = 29/5
Here, we first need to distribute the 3 across the terms within the parentheses:
3x + 54/10 = 29/5
Then, simplify the fraction 54/10 (to 27/5) and proceed with the steps outlined above to isolate and solve for x.
Equations with Decimals
The problem could also be presented using decimals instead of fractions:
x + 1.8 = 5.8
The solution process remains the same. Subtract 1.8 from both sides to find x.
Practical Applications of Solving Algebraic Equations
Solving algebraic equations isn't just an academic exercise; it has wide-ranging practical applications in various fields:
- Engineering: Calculating forces, stresses, and strains in structural analysis.
- Physics: Determining velocities, accelerations, and other physical quantities.
- Finance: Modeling financial growth, calculating interest rates, and analyzing investments.
- Computer Science: Developing algorithms, optimizing code, and creating simulations.
- Chemistry: Determining concentrations, reaction rates, and equilibrium constants.
- Everyday Life: Problems related to budgeting, recipe scaling, and distance/time calculations all involve similar algebraic principles.
Tips and Tricks for Solving Algebraic Equations
- Always simplify: Simplifying fractions and decimals at the beginning will make the calculations much smoother.
- Keep it balanced: Whatever you do to one side of the equation, always do the same to the other side.
- Check your work: Substitute your solution back into the original equation to verify its accuracy.
- Practice regularly: The more you practice, the more comfortable and proficient you'll become.
- Break down complex problems: Divide complicated equations into smaller, more manageable steps.
- Use visualization: Drawing diagrams or charts can help visualize the problem and understand the relationships between variables.
Conclusion
The seemingly simple equation "18/10 more than a number x is equal to 29/5" serves as a springboard to understanding a fundamental principle in algebra. By mastering the techniques outlined in this article, you'll develop the skills to confidently tackle more complex algebraic problems and apply these skills to diverse real-world situations. Remember, the key lies in understanding the principles, practicing diligently, and always verifying your solutions. With consistent effort, you can confidently navigate the world of algebraic equations and unlock their practical power.
Latest Posts
Latest Posts
-
Which Writing Element Affects The Tone Of The Text
Jun 06, 2025
-
Bob Is Reading A Chemical Manufacturer Label
Jun 06, 2025
-
David Is Buying A New Car For 21349
Jun 06, 2025
-
The Difference Of 12 And 20 Of A Number X
Jun 06, 2025
-
If You Were Constructing An Audience Analysis Questionnaire
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about 18/10 More Than A Number X Is Equal To 29/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.