2 2i 4 3i 7 8i
Breaking News Today
Jun 04, 2025 · 5 min read
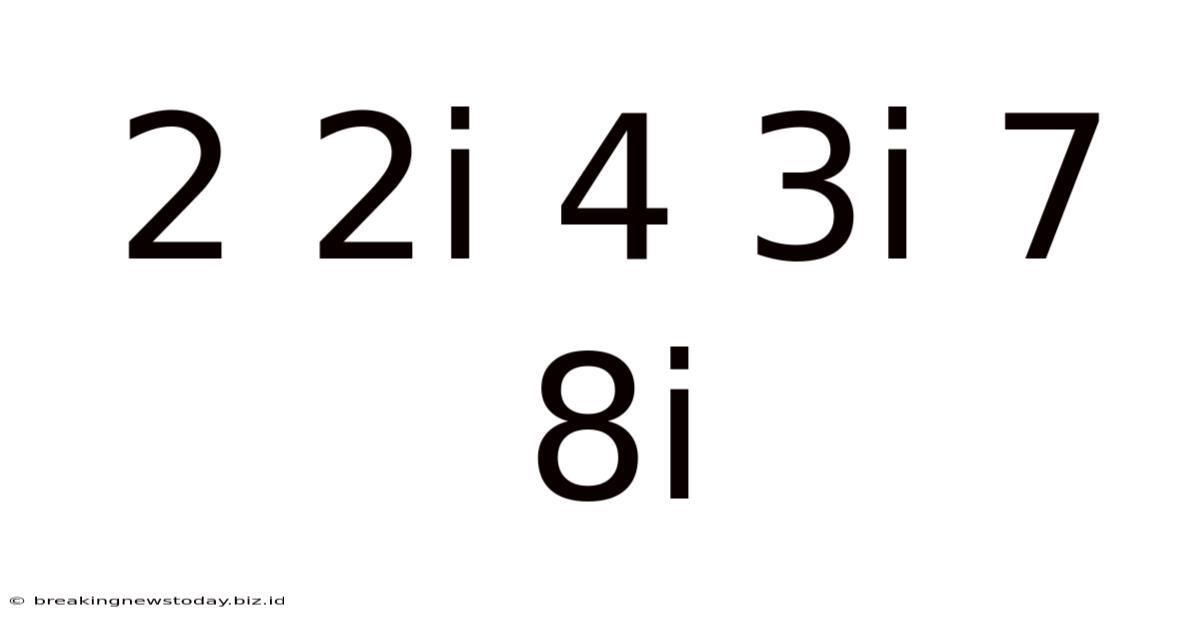
Table of Contents
Decoding the Sequence: 2, 2i, 4, 3i, 7, 8i... and Beyond
The seemingly simple sequence, 2, 2i, 4, 3i, 7, 8i..., presents a fascinating puzzle. At first glance, it appears chaotic, a random scattering of integers and imaginary numbers. However, a closer examination reveals an underlying pattern, a hidden logic waiting to be uncovered. This article will delve deep into this sequence, exploring its potential structures, generating methods, and applications, showcasing how mathematical curiosity can unravel even the most perplexing enigmas.
Unraveling the Pattern: Real and Imaginary Components
The sequence interleaves real numbers (2, 4, 7, ...) and imaginary numbers (2i, 3i, 8i, ...). This immediately suggests we should analyze the real and imaginary components separately.
The Real Number Sequence: 2, 4, 7...
Let's focus on the real numbers: 2, 4, 7... The differences between consecutive terms are:
- 4 - 2 = 2
- 7 - 4 = 3
The differences themselves form a sequence: 2, 3... This suggests a pattern where the differences between consecutive real numbers are increasing integers. Therefore, we can predict the next real number in the sequence:
- Next difference: 4
- Next real number: 7 + 4 = 11
This gives us an extended real number sequence: 2, 4, 7, 11... This is a quadratic sequence, meaning the second differences are constant (in this case, 1). A general formula for this type of sequence can be derived. However, for the sake of simplicity, we'll observe the pattern and extrapolate rather than delve into the formal derivation of the quadratic formula.
The Imaginary Number Sequence: 2i, 3i, 8i...
The imaginary number sequence is: 2i, 3i, 8i... The coefficients of 'i' form another sequence: 2, 3, 8... The differences are:
- 3 - 2 = 1
- 8 - 3 = 5
This sequence of differences (1, 5...) doesn't immediately reveal a clear pattern as simply increasing integers. This suggests a more complex relationship or a different underlying pattern altogether.
Exploring Potential Generation Methods
Several possible approaches could generate the complete sequence:
1. Recursive Definition: A recursive definition would define each term based on the preceding terms. This would require finding a relationship between the real and imaginary components and their respective predecessors. This approach might involve multiple recursive relationships, one for the real parts and another for the imaginary parts. While theoretically possible, finding such a relationship requires sophisticated mathematical analysis.
2. Piecewise Function: A piecewise function could be defined separately for the real and imaginary components. The real component might follow the quadratic relationship we identified earlier. For the imaginary component, we might need a more complex formula, potentially involving exponentials or other non-linear functions. Experimentation and curve-fitting techniques could help to find an appropriate function to match the existing data.
3. Combination of Functions: It's also possible that the entire sequence is generated by a combination of functions. For example, one function could dictate the real components, while another function, possibly dependent on the real component, generates the imaginary component. This interdependent generation could produce the interwoven pattern observed.
Mathematical Analysis and Potential Applications
The mathematical analysis of this sequence would benefit from the use of more data points. The currently available data is insufficient to definitively determine a single, elegant mathematical function or recursion to generate all subsequent terms. Additional terms would significantly aid in confirming or refuting the hypothesized patterns and potentially reveal a simpler, more concise mathematical representation.
However, even with the limited data, we can speculate on potential applications within various mathematical fields:
-
Number Theory: The sequence could be explored within the context of number theory, seeking relationships between prime numbers, composite numbers, or other number-theoretic properties. The presence of both real and imaginary numbers suggests possible applications involving complex number theory.
-
Chaos Theory: The seemingly random nature of the sequence could pique interest in chaos theory, investigating if it exhibits characteristics of deterministic chaos or if it's truly random. Further terms are crucial for understanding the long-term behavior.
-
Signal Processing: The alternating real and imaginary components could represent a signal, with possible applications in areas such as digital signal processing or communications engineering. Analyzing the frequency content and other signal properties could uncover further insights.
-
Abstract Algebra: The sequence might have connections to abstract algebraic structures, such as groups or rings. This would necessitate a much deeper investigation into the underlying relationships between the terms.
Further Investigation and Conclusion
The sequence 2, 2i, 4, 3i, 7, 8i... offers an engaging challenge for mathematicians and anyone fascinated by number patterns. While a definitive solution or generating function remains elusive based on the limited data provided, the analysis points to several avenues of exploration. Continued investigation, including finding further terms in the sequence, will be vital in uncovering the complete and accurate mathematical description of this enigmatic sequence. The interleaving of real and imaginary numbers suggests a richer complexity than initially apparent, possibly involving multiple interdependent functions or recursive relationships. The journey of uncovering its secrets highlights the beauty and persistent challenge inherent in mathematical problem-solving. Further research is strongly encouraged to unlock the full potential of this intriguing mathematical puzzle.
The inherent ambiguity underscores the importance of having a sufficient amount of data to make valid conclusions. This is a testament to the scientific method, where hypothesis formation must be rigorously tested and validated through empirical evidence. The pursuit of understanding this sequence illustrates the dynamic interplay between observation, hypothesis, and verification in the field of mathematics. It encourages a spirit of inquiry and highlights the often-surprising connections between seemingly disparate mathematical concepts.
Latest Posts
Latest Posts
-
Ba Express Your Answer As An Integer
Jun 05, 2025
-
Which Sentence Best Explains The Reason For Pandoras Fall
Jun 05, 2025
-
Complete These Sentences About The Setting Of Wuthering Heights
Jun 05, 2025
-
Which Sentences Contain A Comma Splice Check All That Apply
Jun 05, 2025
-
Which Of The Following Statements Is True Of Hair Care
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 2 2i 4 3i 7 8i . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.