2 3y 6 3 4 Y
Breaking News Today
Jun 01, 2025 · 5 min read
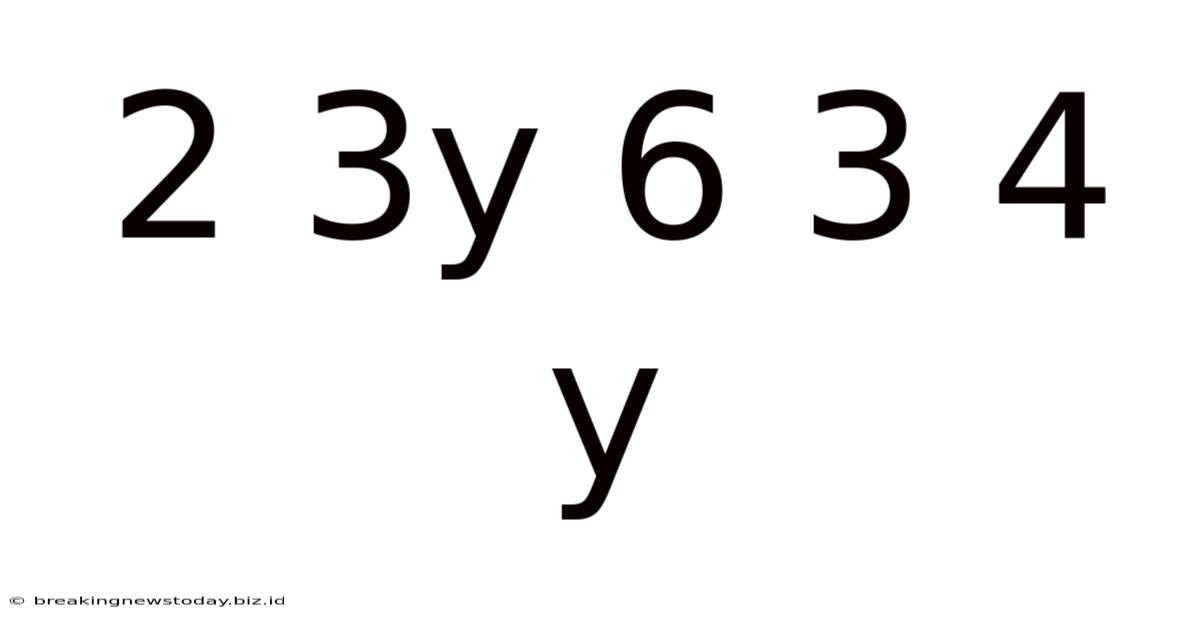
Table of Contents
Decoding the Sequence: 2 3y 6 3 4 y – A Deep Dive into Pattern Recognition and Mathematical Possibilities
The seemingly simple sequence "2 3y 6 3 4 y" presents a fascinating challenge: deciphering its underlying pattern. While there's no single definitive answer without additional context, we can explore several plausible interpretations, utilizing various mathematical and logical approaches. This exploration will delve into pattern recognition techniques, discuss potential solutions, and highlight the importance of context in problem-solving. The journey will touch upon concepts applicable in various fields, from cryptography to data analysis.
Understanding the Problem: The Importance of Context
The key to unlocking the mystery of "2 3y 6 3 4 y" lies in understanding the potential context. Is this a code? A mathematical sequence? Part of a larger puzzle? Without further information, multiple interpretations become valid. This ambiguity underscores the importance of context in problem-solving, a crucial concept in many fields. For example, in cryptography, a code's meaning hinges entirely on the key or algorithm used. Similarly, in data analysis, understanding the source and nature of the data is essential for accurate interpretation.
Possible Interpretations and Solutions
Let's explore several potential interpretations and solutions, keeping in mind the inherent uncertainty without additional information.
1. Alternating Sequences:
One possible interpretation is that the sequence consists of two interwoven sequences: one numerical and one alphanumeric.
-
Numerical Sequence: 2, 6, 4. This sequence is less straightforward to decipher without more data points. It could be part of a larger arithmetic or geometric progression, or it could represent something entirely different (e.g., indices within a larger dataset).
-
Alphanumeric Sequence: 3y, 3, y. This sequence is equally ambiguous. The 'y' could represent a variable, a placeholder, a specific value, or even an intentional distraction. Without more information, it's difficult to draw definitive conclusions.
Analysis: This interpretation is plausible, but it lacks a clear, unifying mathematical or logical rule connecting the two subsequences.
2. Base Conversion or Code:
Another possibility is that the sequence represents a number or message encoded using a non-standard base or cipher.
-
Exploring Different Bases: We could attempt to convert the numerical portions (2, 6, 4) into different number bases (binary, ternary, etc.) to see if any pattern emerges. However, without knowing the base, this approach is largely speculative.
-
Considering Simple Substitutions: The 'y' could be a simple substitution for a digit or a symbol within a coded message. We could try substituting 'y' with various characters (0-9, A-Z) and look for patterns in the resulting sequence. This method, however, would involve a large amount of trial and error.
Analysis: This approach requires making significant assumptions about the encoding scheme, making definitive conclusions highly challenging.
3. Recursive or Iterative Pattern:
The sequence could be generated using a recursive or iterative process.
-
Searching for Recursion: We could explore the possibility of a recursive function that generates the sequence. However, devising such a function without more data points is exceptionally difficult. It's highly likely that a recursive solution, if it exists, would involve several parameters that aren't immediately apparent.
-
Identifying Iterative Rules: Similar to the recursive approach, an iterative rule could define the sequence. This could involve mathematical operations on preceding terms, generating the next term in the sequence. The problem is, the sequence is too short to confidently determine such a rule.
Analysis: While this approach is plausible, the limited length of the sequence makes it difficult to pinpoint a definitive recursive or iterative rule.
4. Mathematical Functions and Operations:
A more abstract approach involves considering mathematical functions that could potentially generate the sequence.
-
Exploring Polynomial Functions: Higher-order polynomial functions might fit the existing sequence points, but this would be a purely curve-fitting exercise. Without more data points, any derived function would be highly speculative and likely not generalize well to future terms in the sequence.
-
Considering Trigonometric or Logarithmic Functions: Similarly, trigonometric or logarithmic functions could potentially model the sequence. Again, without additional data, it's unlikely that a satisfactory solution would be found.
Analysis: This approach requires considerable mathematical expertise and is computationally intensive without sufficient data to constrain the solution space.
Expanding the Possibilities: The Need for More Data
The limited length of the sequence ("2 3y 6 3 4 y") significantly restricts our ability to confidently determine its underlying pattern. To effectively analyze and solve this puzzle, we need significantly more data points. A longer sequence would provide more information to test different hypotheses and eliminate inconsistencies.
For example, if the sequence were extended to "2 3y 6 3 4 y 8 5 z 10...", we could explore more patterns and potentially rule out some of the previously mentioned possibilities. The additional 'z' and numbers would provide crucial information about the nature of the alphanumeric and numeric subsequences.
The Role of Contextual Information
The absence of contextual information severely hampers our ability to solve this puzzle. Knowing the source of the sequence, the intended purpose (e.g., code, puzzle, mathematical problem), or the field of study from which it originates would dramatically enhance our ability to decipher it.
Conclusion: The Importance of Pattern Recognition and Problem-Solving Techniques
The sequence "2 3y 6 3 4 y" serves as a prime example of the challenges and rewards of pattern recognition. While we've explored various possibilities, the lack of sufficient data and context makes definitive conclusions impossible. This exercise highlights the need for careful consideration of various problem-solving strategies and the critical role that context plays in accurately interpreting data. Future analysis would depend heavily on acquiring additional data and understanding the context surrounding this sequence. The key takeaway is that robust pattern recognition often requires more information than initially presented. The ability to adapt strategies and consider multiple interpretations is a valuable skill in solving complex problems across diverse fields.
Latest Posts
Latest Posts
-
Which Best Describes The Homes In Which Peasants Lived
Jun 02, 2025
-
Trusting Ones Self Goals And Progress
Jun 02, 2025
-
High Fiber Diets Are Associated With All Of The Following Except
Jun 02, 2025
-
An Endemic Species Inhabiting Sierra Gorda
Jun 02, 2025
-
Simpson And Brown Company File Cabinet Answers
Jun 02, 2025
Related Post
Thank you for visiting our website which covers about 2 3y 6 3 4 Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.