2 N 1 4n 2 3n 1
Breaking News Today
Jun 06, 2025 · 5 min read
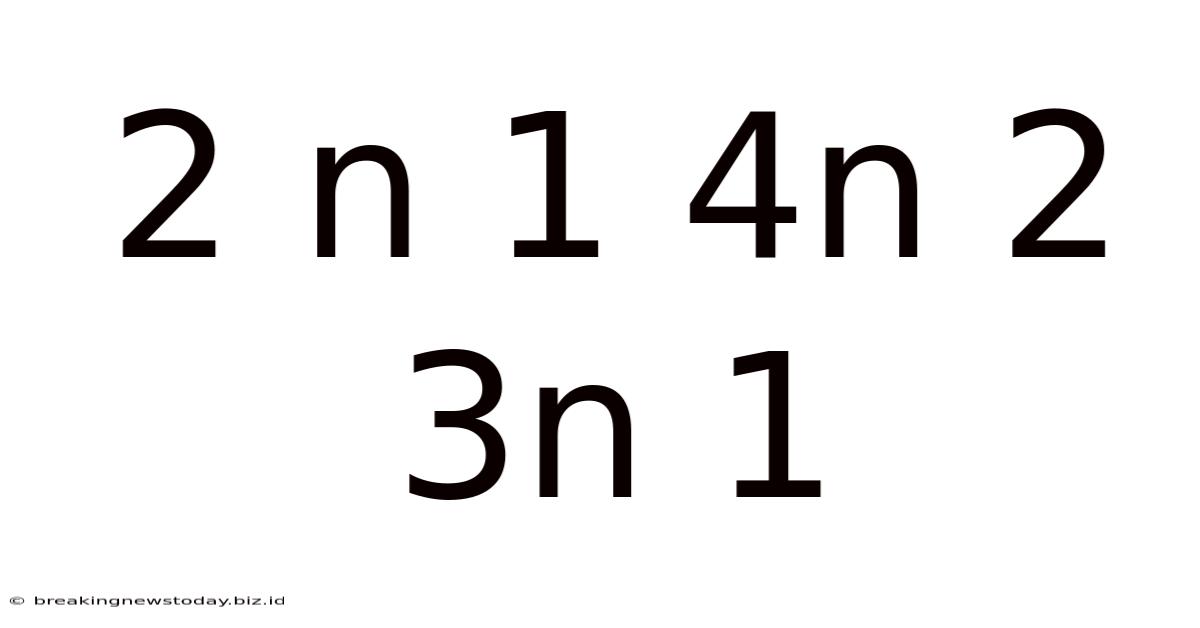
Table of Contents
Decoding the Collatz Conjecture: Exploring 3n+1 and its Mysteries
The seemingly simple mathematical problem known as the Collatz Conjecture, also called the 3n+1 problem, the 3x+1 problem, the Syracuse problem, Kakutani's problem, Thwaites' conjecture, or the Hasse algorithm, continues to baffle mathematicians worldwide. Despite its straightforward formulation, proving or disproving this conjecture remains one of the most elusive challenges in mathematics. This article delves into the intricacies of the 3n+1 problem, exploring its fundamental rules, observed patterns, and the ongoing quest for its solution.
Understanding the Rules of the Game: 3n+1
The Collatz Conjecture centers around a deceptively simple iterative process:
-
Start with any positive integer. Let's call this number n.
-
If n is even, divide it by 2 (n/2).
-
If n is odd, multiply it by 3 and add 1 (3n+1).
-
Repeat steps 2 and 3 with the resulting number.
The conjecture states that no matter what positive integer you start with, this process will eventually reach the number 1. Once it reaches 1, the sequence continues in a predictable loop: 1, 4, 2, 1, 4, 2...
Let's illustrate with a few examples:
Example 1: Starting with 6
- 6 (even) → 3 (odd) → 10 (even) → 5 (odd) → 16 (even) → 8 (even) → 4 (even) → 2 (even) → 1
Example 2: Starting with 11
- 11 (odd) → 34 (even) → 17 (odd) → 52 (even) → 26 (even) → 13 (odd) → 40 (even) → 20 (even) → 10 (even) → 5 (odd) → 16 (even) → 8 (even) → 4 (even) → 2 (even) → 1
The Allure of the Infinite: Why is it So Difficult?
Despite its apparent simplicity, proving the Collatz Conjecture has eluded mathematicians for decades. The challenge lies in the unpredictable nature of the sequence. While the process seems straightforward, the numbers generated can jump wildly, making it difficult to find a general pattern or proof that holds for all positive integers.
The Problem of Unpredictability
The sequence generated by the Collatz process is highly sensitive to the starting number. Small changes in the initial value can lead to dramatically different sequences, making it nearly impossible to predict the behavior of the process for arbitrarily large numbers. This unpredictability is at the heart of the difficulty in proving the conjecture.
The Absence of a Clear Pattern
While extensive computational testing has shown that the conjecture holds true for an incredibly large range of numbers (up to numbers with trillions of digits), this does not constitute a mathematical proof. A proof requires demonstrating that the conjecture holds for all positive integers, not just a finite subset. The lack of an easily discernible pattern in the generated sequences makes finding such a universal proof exceptionally challenging.
Exploring the Depths: Advanced Concepts and Research
While a definitive proof remains elusive, researchers have made significant progress in understanding the properties of the Collatz process. Here are some key areas of ongoing research:
1. Statistical Analysis and Probability
Statistical methods have been used to analyze the behavior of the Collatz sequences. These studies have shown that, on average, the sequences tend to decrease in magnitude. This observation supports the conjecture but doesn't provide a rigorous proof.
2. Cycle Detection and Loops
A crucial aspect of the conjecture is the eventual convergence to the 1-4-2-1 loop. Research focuses on proving that no other cycles exist within the process. The absence of other cycles would strongly support the conjecture.
3. Computational Explorations
Massive computational resources have been dedicated to testing the conjecture for increasingly larger numbers. While these tests haven't found any counterexamples, they can't definitively prove the conjecture's validity for all infinitely many numbers.
4. Connections to Other Mathematical Fields
Researchers are exploring potential links between the Collatz Conjecture and other areas of mathematics, such as dynamical systems, number theory, and graph theory. These connections may offer alternative approaches to proving or disproving the conjecture.
The Significance of the 3n+1 Problem
The enduring appeal of the Collatz Conjecture stems not only from its inherent mathematical elegance but also from its accessibility. Its simple rules can be understood by anyone with basic arithmetic knowledge, yet its solution remains beyond the grasp of some of the brightest minds in the field.
This accessibility has made the conjecture a popular subject for recreational mathematics and amateur exploration. The challenge it poses inspires countless individuals to delve into the world of mathematical research, fostering creativity and critical thinking. Furthermore, the pursuit of a solution pushes the boundaries of mathematical tools and techniques, potentially leading to advancements in other areas of mathematics and computer science.
The Continued Quest: The Future of the 3n+1 Problem
Despite the lack of a definitive proof, the Collatz Conjecture continues to be an active area of research. Mathematicians are constantly developing new tools and approaches in the hope of finally cracking this long-standing problem.
Open Questions and Future Directions
Several open questions remain regarding the Collatz Conjecture:
-
Does every positive integer eventually reach 1? This is the core question of the conjecture.
-
Are there any other cycles besides the 1-4-2-1 loop? Proving the absence of other cycles is crucial.
-
What is the average stopping time for a given number? Understanding the average number of steps required to reach 1 would provide valuable insights.
-
Can we find a closed-form expression to predict the behavior of the sequence? Such an expression would greatly simplify the analysis of the conjecture.
The search for a solution continues, driving innovation in mathematical reasoning and computational techniques. The 3n+1 problem stands as a testament to the power and enduring mystery of mathematics. Its persistence as an unsolved problem keeps it relevant and captivating to mathematicians and enthusiasts alike. The journey towards a potential solution, rather than the solution itself, may ultimately represent the most significant contribution of this fascinating problem. The continued exploration and analysis, coupled with the development of novel approaches, serve to strengthen the mathematical landscape and contribute to a broader understanding of complex systems and computational processes. The legacy of the Collatz Conjecture, therefore, lies not solely in its eventual resolution (should one ever be found), but in its enduring role as a catalyst for mathematical inquiry and advancement.
Latest Posts
Latest Posts
-
How Does The Excerpt Reveal Ophelias Character Development
Jun 06, 2025
-
Which Of The Following Best Describes Physical Science
Jun 06, 2025
-
As A Demographer Sherwood Would Be Most Interested In Studying
Jun 06, 2025
-
Which Is The Most Likely Prototype For The Concept Vehicle
Jun 06, 2025
-
Choosing Never To Sky Dive Is An Example Of Risk
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about 2 N 1 4n 2 3n 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.