2 Times The Difference Between 49.5 And 37.5
Breaking News Today
Jun 01, 2025 · 5 min read
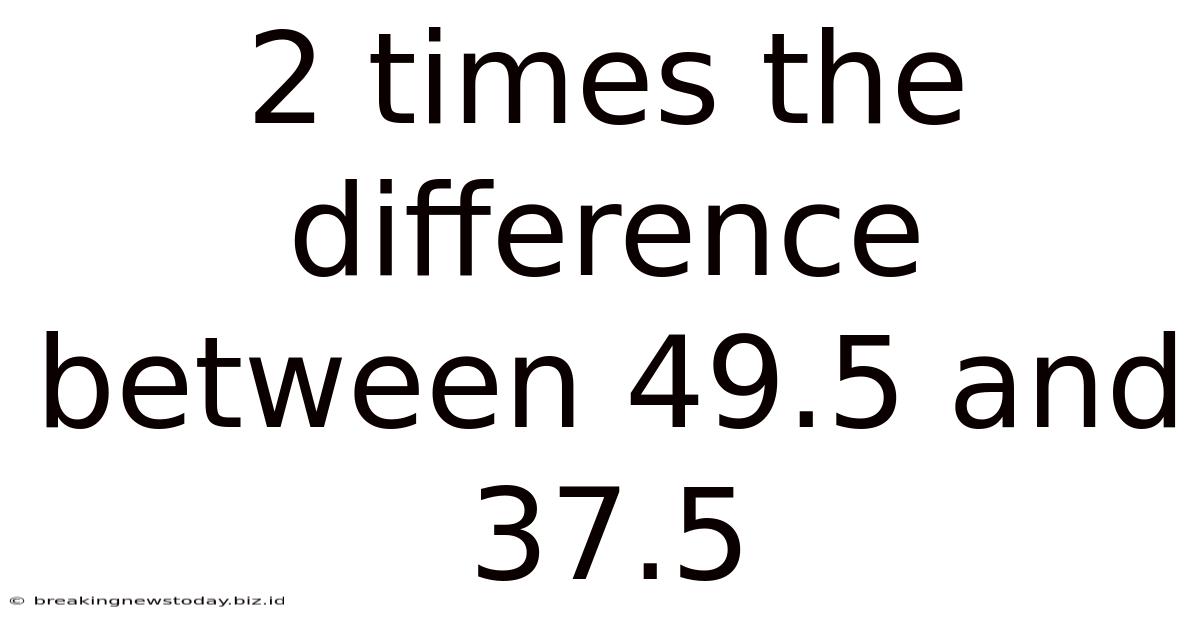
Table of Contents
2 Times the Difference Between 49.5 and 37.5: A Deep Dive into Mathematical Concepts and Applications
This seemingly simple mathematical problem – finding 2 times the difference between 49.5 and 37.5 – opens the door to exploring fundamental mathematical concepts and their practical applications across various fields. While the calculation itself is straightforward, understanding the underlying principles and exploring related topics enriches our comprehension of mathematics and its relevance in the real world.
Understanding the Problem: A Step-by-Step Approach
The problem statement asks us to perform two key operations: finding the difference and then multiplying that difference by two. Let's break down the process:
1. Finding the Difference:
The first step involves subtracting the smaller number (37.5) from the larger number (49.5). This difference represents the numerical gap between the two values.
49.5 - 37.5 = 12
2. Doubling the Difference:
The second step instructs us to multiply the difference we calculated (12) by two.
12 * 2 = 24
Therefore, the solution to the problem "2 times the difference between 49.5 and 37.5" is 24.
Expanding the Horizons: Exploring Related Mathematical Concepts
This simple calculation provides a springboard to delve into more complex mathematical ideas. Let's explore some of them:
1. Number Systems and Operations:
The numbers used in this problem (49.5, 37.5, 12, 24) belong to the real number system, a set that includes all rational and irrational numbers. Understanding different number systems (integers, rational numbers, irrational numbers, real numbers, complex numbers) is crucial for advanced mathematical applications. The operations performed – subtraction and multiplication – are fundamental arithmetic operations that form the basis of more complex algebraic manipulations.
2. Algebraic Expressions and Equations:
We can represent this problem using algebraic expressions. Let's say 'x' represents the first number (49.5) and 'y' represents the second number (37.5). The problem can then be expressed as:
2 * (x - y)
Substituting the values:
2 * (49.5 - 37.5) = 24
This representation allows us to generalize the problem and apply it to other sets of numbers. Moreover, it lays the groundwork for solving more complex algebraic equations.
3. Functions and Mapping:
The process of finding the difference and then doubling it can be viewed as a function. A function maps an input (in this case, a pair of numbers) to an output (the result of the calculation). We can define a function, f(x,y), as:
f(x,y) = 2 * (x - y)
This function takes two inputs (x and y) and returns a single output. Understanding functions is essential in calculus, linear algebra, and numerous other areas of mathematics.
4. Geometry and Measurement:
Imagine two line segments with lengths 49.5 units and 37.5 units. The difference between their lengths represents the length of a third line segment. Doubling this difference would represent the length of another line segment twice as long. This simple problem, therefore, has geometric interpretations relevant in fields like surveying, architecture, and engineering.
5. Statistics and Data Analysis:
In statistics, the difference between two values might represent a change or variation. For example, if 49.5 and 37.5 represent measurements at two different time points, the difference would be the change in the measured quantity. Doubling the difference might be relevant in scenarios involving projections or estimations based on observed changes. This concept is crucial in fields like economics, finance, and environmental science where trends and changes are constantly analyzed.
6. Percentage Change and Rate of Change:
The difference between 49.5 and 37.5 can be expressed as a percentage change. The percentage change is calculated as:
[(49.5 - 37.5) / 37.5] * 100% = 32%
This indicates that 49.5 is 32% greater than 37.5. Understanding percentage change is vital in various applications, including finance (calculating returns on investments), economics (measuring economic growth), and many other fields. The rate of change—how quickly a value is changing over time—is a more complex concept often introduced in calculus, built upon similar principles.
Real-World Applications: Where This Calculation Matters
The seemingly simple calculation of "2 times the difference between 49.5 and 37.5" finds application in diverse real-world scenarios:
-
Profit Calculation: Imagine a business with initial costs of 37.5 units and revenue of 49.5 units. The difference represents the profit, and doubling the profit might represent projected profits under certain conditions.
-
Inventory Management: If a warehouse starts with 37.5 units of a product and ends the period with 49.5 units, the difference represents net increase in stock. Doubling this might represent a target stock increase for the next period.
-
Financial Analysis: In financial modeling, this calculation might be part of a larger analysis involving projections, risk assessment, or portfolio optimization.
-
Scientific Measurements: In scientific experiments, the difference between two measurements might represent an experimental error or a change in a quantity being measured (e.g., temperature, pressure, or volume). Doubling the difference could be relevant in error analysis or in extrapolating findings.
-
Engineering and Design: In engineering and design, this calculation might be used in various calculations related to dimensions, material quantities, or tolerances.
Beyond the Numbers: Critical Thinking and Problem-Solving
This simple problem emphasizes the importance of critical thinking and problem-solving skills. It's not just about arriving at the answer (24) but also about understanding the underlying steps, the mathematical concepts involved, and the potential applications in different contexts. This approach to problem-solving is valuable in various academic and professional fields.
Conclusion: The Power of Simple Mathematics
The problem of finding "2 times the difference between 49.5 and 37.5" provides a seemingly simple yet powerful illustration of fundamental mathematical concepts and their far-reaching applications. While the numerical solution is straightforward, the journey of exploring related mathematical ideas and their practical relevance reveals the beauty and utility of mathematics in the real world. Understanding these fundamental principles enhances critical thinking, problem-solving abilities, and the capacity to tackle more complex mathematical challenges. The simplicity of the initial problem belies the depth and breadth of mathematical knowledge it can unlock. This exploration underscores the importance of a solid mathematical foundation for success in various academic and professional pursuits.
Latest Posts
Latest Posts
-
Joel Is Laying Pipe For A Sprinkler System
Jun 02, 2025
-
An Example Of Deductive Reasoning Is Shown In The
Jun 02, 2025
-
Inadvertent Actions Such As Using Easy Passwords
Jun 02, 2025
-
Which Sequence Of Transformations Carries Abcd Onto Hgfe
Jun 02, 2025
-
What Percent Of 32 Is 28
Jun 02, 2025
Related Post
Thank you for visiting our website which covers about 2 Times The Difference Between 49.5 And 37.5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.