20 Of What Number Is Equal To 5 Of 680
Breaking News Today
Jun 08, 2025 · 4 min read
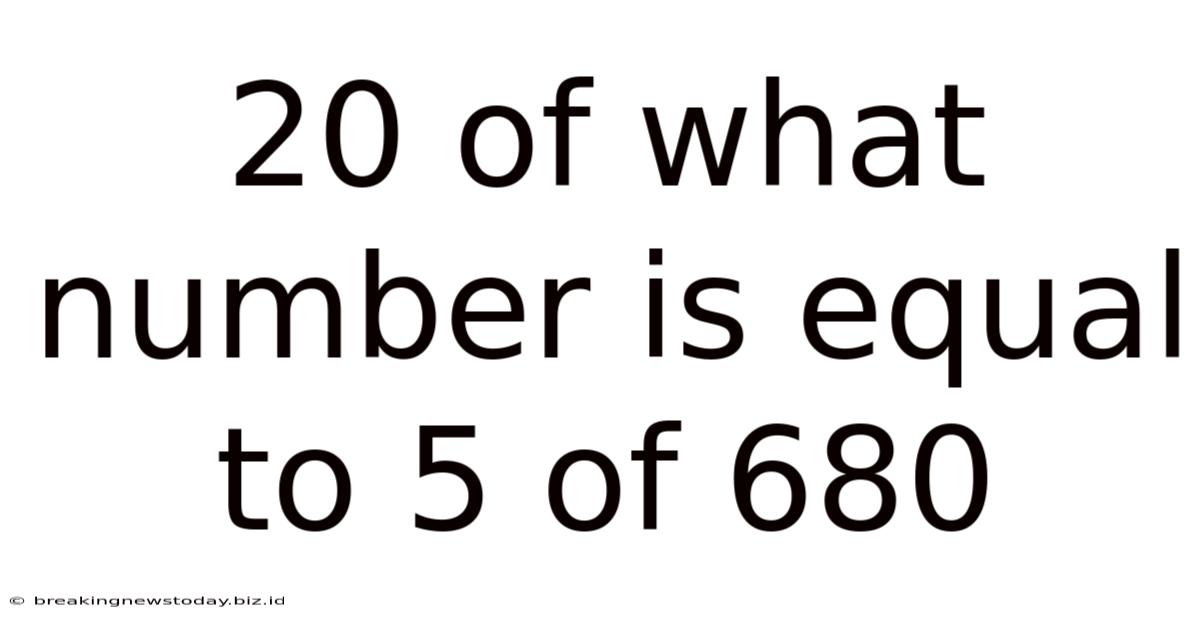
Table of Contents
20 of What Number is Equal to 5 of 680? Solving the Proportion and Exploring Related Concepts
This seemingly simple math problem, "20 of what number is equal to 5 of 680," hides a wealth of mathematical concepts and problem-solving strategies. Let's dive deep into solving this problem, exploring the underlying principles, and expanding our understanding of proportions and related mathematical ideas.
Understanding the Problem: Setting up the Equation
The core of this problem lies in understanding proportions. A proportion is a statement that two ratios are equal. We can express this problem as a proportion:
20/x = 5/680
Where:
- 20 represents the first part of the ratio.
- x represents the unknown number we're trying to find.
- 5 represents the second part of the ratio.
- 680 represents the whole of the second ratio.
This equation states that the ratio of 20 to x is equal to the ratio of 5 to 680.
Solving the Proportion: Cross-Multiplication and Simplification
To solve for x, we use the powerful technique of cross-multiplication. This involves multiplying the numerator of one ratio by the denominator of the other, and setting the products equal to each other.
20 * 680 = 5 * x
Now we have a simple algebraic equation:
13600 = 5x
To isolate x, we divide both sides of the equation by 5:
x = 13600 / 5
x = 2720
Therefore, 20 of 2720 is equal to 5 of 680.
Verifying the Solution
It's always good practice to check our answer. Let's verify if our solution is correct:
- 20/2720 = 0.00735 (approximately)
- 5/680 = 0.00735 (approximately)
The ratios are indeed equal, confirming that our solution, x = 2720, is correct.
Expanding the Concept: Proportions in Everyday Life
Proportions are not just abstract mathematical concepts; they're fundamental to many aspects of our daily lives. We encounter them in:
- Cooking: Scaling up or down recipes. If a recipe calls for 2 cups of flour for 4 servings, how much flour is needed for 6 servings?
- Mapping: Understanding scale. A map with a scale of 1:100,000 means that 1 cm on the map represents 100,000 cm (or 1 km) in reality.
- Construction: Calculating material needs. If a certain amount of material is needed for a specific length, how much is required for a longer length?
- Finance: Calculating interest, discounts, or exchange rates.
- Science: Analyzing data and conducting experiments.
Beyond Simple Proportions: Exploring More Complex Scenarios
While this problem involved a straightforward proportion, the underlying principles can be applied to more complex scenarios. Consider these extensions:
1. Percentage Calculations:
The problem can be rephrased as a percentage problem: "20 is what percentage of 2720?" To find this, we would use the formula:
(Part / Whole) * 100%
(20 / 2720) * 100% = 0.735% (approximately)
This shows that 20 is approximately 0.735% of 2720. Similarly, 5 is approximately 0.735% of 680.
2. Proportions with Three Variables:
Imagine a similar problem but with three variables: "20 of what number is equal to 5 of what number, knowing the total of both numbers is 3400?". Solving this would require setting up a system of two equations with two unknowns and solving simultaneously.
3. Inverse Proportions:
Instead of a direct proportion, sometimes we encounter inverse proportions. For example, the time it takes to complete a task is inversely proportional to the number of people working on it. More people means less time.
Practical Applications and Real-World Examples:
The ability to solve proportions is essential in many fields:
- Engineering: Calculating load-bearing capacities of structures, designing efficient systems.
- Medicine: Determining drug dosages based on patient weight.
- Business: Forecasting sales, managing inventory, determining pricing strategies.
- Graphics and Design: Scaling images and designs while maintaining aspect ratio.
Developing Problem-Solving Skills: Tips and Strategies
Solving problems like "20 of what number is equal to 5 of 680" is not just about finding the answer; it's about developing crucial problem-solving skills. Here are some key strategies:
- Read Carefully: Understand exactly what the problem is asking.
- Identify Key Information: Extract the relevant numbers and relationships.
- Choose the Right Method: Select the appropriate mathematical tools (proportions, equations, percentages).
- Show Your Work: Clearly document each step of your solution process.
- Check Your Answer: Verify the solution to ensure it makes sense in the context of the problem.
- Practice Regularly: Consistent practice is key to mastering mathematical problem-solving.
Conclusion: Mastering Proportions for a Stronger Mathematical Foundation
The seemingly simple problem, "20 of what number is equal to 5 of 680," serves as a gateway to understanding proportions and their applications. By grasping the concepts and techniques discussed here, you'll not only solve this specific problem but also build a strong foundation for tackling more complex mathematical challenges in various fields. Remember that practice is key to mastering these skills, and the applications of these principles extend far beyond the classroom into everyday life and various professional settings. So, keep practicing, keep exploring, and keep expanding your mathematical horizons!
Latest Posts
Latest Posts
-
What Number Sentence Does This Model Show
Jun 08, 2025
-
Brake Fluid Expands And Contracts With Changes In Temperature
Jun 08, 2025
-
A Number Cube Numbered 1 6 Is Rolled Once
Jun 08, 2025
-
Which Sentence Is The Clearest Example Of Alliteration
Jun 08, 2025
-
What Is The Value Of The Underlined Digit 56
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about 20 Of What Number Is Equal To 5 Of 680 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.