20x 5y 15 Solve For Y
Breaking News Today
Jun 06, 2025 · 5 min read
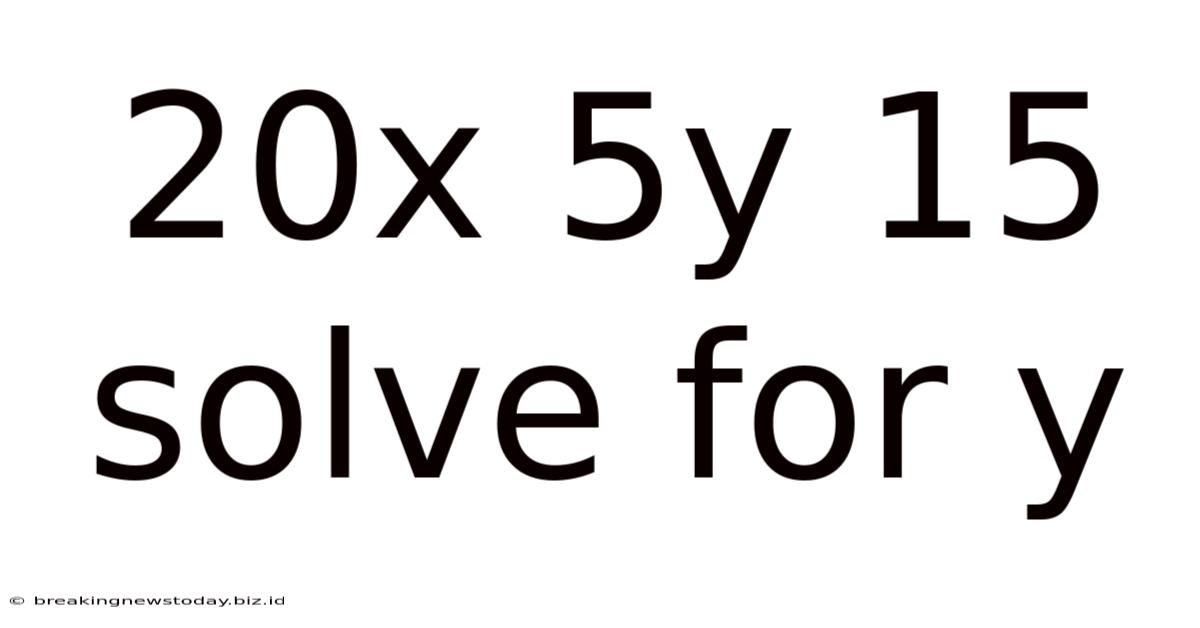
Table of Contents
Solving for y: A Comprehensive Guide to 20x + 5y = 15
This article provides a comprehensive guide on how to solve the algebraic equation 20x + 5y = 15 for 'y'. We will explore various methods, delve into the underlying concepts, and offer practical examples to solidify your understanding. This isn't just about finding the solution; it's about understanding the process and applying it to similar problems. We will also touch upon the implications of this equation in different contexts, highlighting its significance in fields like mathematics, physics, and economics.
Understanding the Equation: 20x + 5y = 15
The equation 20x + 5y = 15 is a linear equation in two variables, x and y. A linear equation represents a straight line when graphed on a coordinate plane. The equation shows a relationship between x and y; a change in the value of x will directly impact the value of y, and vice-versa. Solving for 'y' means isolating 'y' on one side of the equation, expressing it in terms of 'x'. This will give us the equation of the line in the slope-intercept form (y = mx + c), where 'm' represents the slope and 'c' represents the y-intercept.
Method 1: Isolating 'y' through Algebraic Manipulation
This is the most straightforward method. We will use basic algebraic operations to isolate 'y'. Here's a step-by-step guide:
-
Subtract 20x from both sides: This eliminates 'x' from the left side, leaving only the term with 'y'. The equation becomes: 5y = 15 - 20x
-
Divide both sides by 5: This isolates 'y' completely. We divide each term on the right side by 5: y = (15 - 20x) / 5
-
Simplify: We can simplify the expression by dividing each term within the parenthesis by 5: y = 3 - 4x
This is the solution. The equation is now in the slope-intercept form (y = mx + c), with a slope (m) of -4 and a y-intercept (c) of 3. This means the line crosses the y-axis at the point (0, 3) and has a negative slope, indicating it slopes downwards from left to right.
Method 2: Using the Properties of Equality
This method emphasizes the underlying properties of equality that allow us to manipulate equations. The core principle is that whatever operation you perform on one side of the equation, you must perform on the other side to maintain the equality. We essentially use the same steps as Method 1, but with a stronger focus on these properties:
-
Subtraction Property of Equality: Subtracting 20x from both sides maintains the equality: 20x + 5y - 20x = 15 - 20x 5y = 15 - 20x
-
Division Property of Equality: Dividing both sides by 5 maintains the equality: 5y / 5 = (15 - 20x) / 5 y = 3 - 4x
This approach reinforces the mathematical foundation behind solving equations.
Graphical Representation and Interpretation
Plotting the equation y = 3 - 4x on a graph helps visualize the solution. The y-intercept is 3, meaning the line passes through the point (0, 3). The slope is -4, meaning for every 1 unit increase in x, y decreases by 4 units. This linear relationship is clearly represented graphically. The graph allows for easy identification of points that satisfy the equation. For example, when x = 1, y = -1; when x = 2, y = -5; and so on.
Applications in Different Fields
The equation 20x + 5y = 15, while seemingly simple, has applications in various fields:
-
Economics: It could represent a budget constraint, where 20x represents the cost of one good (x) and 5y represents the cost of another good (y), with a total budget of 15 units. Solving for y would help determine the maximum amount of good y that can be purchased given a specific quantity of good x.
-
Physics: It might represent a simplified relationship between two physical quantities. For instance, x could represent time and y could represent velocity, with the equation describing the motion of an object under certain conditions.
-
Mathematics: This equation is a fundamental example used to teach concepts like linear equations, slope, intercepts, and solving for variables. It lays the groundwork for more complex mathematical models and analyses.
Solving for 'x'
While the question specifically asks to solve for 'y', it's beneficial to understand how to solve for 'x' as well. This involves similar algebraic manipulations:
-
Subtract 5y from both sides: 20x = 15 - 5y
-
Divide both sides by 20: x = (15 - 5y) / 20
-
Simplify: x = (3 - y) / 4
Handling Different Forms of the Equation
Sometimes, the equation might be presented in a slightly different form. For example, it could be written as:
5y + 20x = 15
or
20x + 5y - 15 = 0
In these cases, the same principles apply. You can rearrange the equation to isolate 'y' using the same algebraic methods outlined earlier.
Advanced Concepts and Extensions
This simple equation serves as a springboard for understanding more complex algebraic concepts. Here are a few extensions:
-
Systems of Linear Equations: The equation can be part of a system of linear equations, requiring simultaneous solutions. This often involves methods like substitution or elimination.
-
Linear Programming: In optimization problems, this equation might represent a constraint, limiting the possible solutions.
-
Calculus: The equation can be used to illustrate concepts in calculus, such as finding the slope of the line (which is a constant in this case).
Conclusion
Solving the equation 20x + 5y = 15 for 'y' is a fundamental exercise in algebra. Through algebraic manipulation and understanding the properties of equality, we arrive at the solution y = 3 - 4x. This simple equation, however, provides a solid foundation for understanding more complex mathematical concepts and has applications in various disciplines. Mastering the techniques presented here is crucial for success in further mathematical studies and practical problem-solving. Remember to practice regularly and explore different variations of this problem to solidify your understanding. The ability to solve such equations efficiently is a valuable skill across many academic and professional fields.
Latest Posts
Latest Posts
-
Unit 1 Equations And Inequalities Homework 3 Solving Equations
Jun 07, 2025
-
Which Best Describes How The Setting Influences Hacknesss Beliefs
Jun 07, 2025
-
Identify An Accurate Statement About Pityriasis Steatoides
Jun 07, 2025
-
Which Of The Following Is True About Gothic Master Builders
Jun 07, 2025
-
A Barrier With Yellow And Purple Markings Indicates A
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 20x 5y 15 Solve For Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.