2311 Divided By 20 With Remainder
Breaking News Today
Jun 02, 2025 · 5 min read
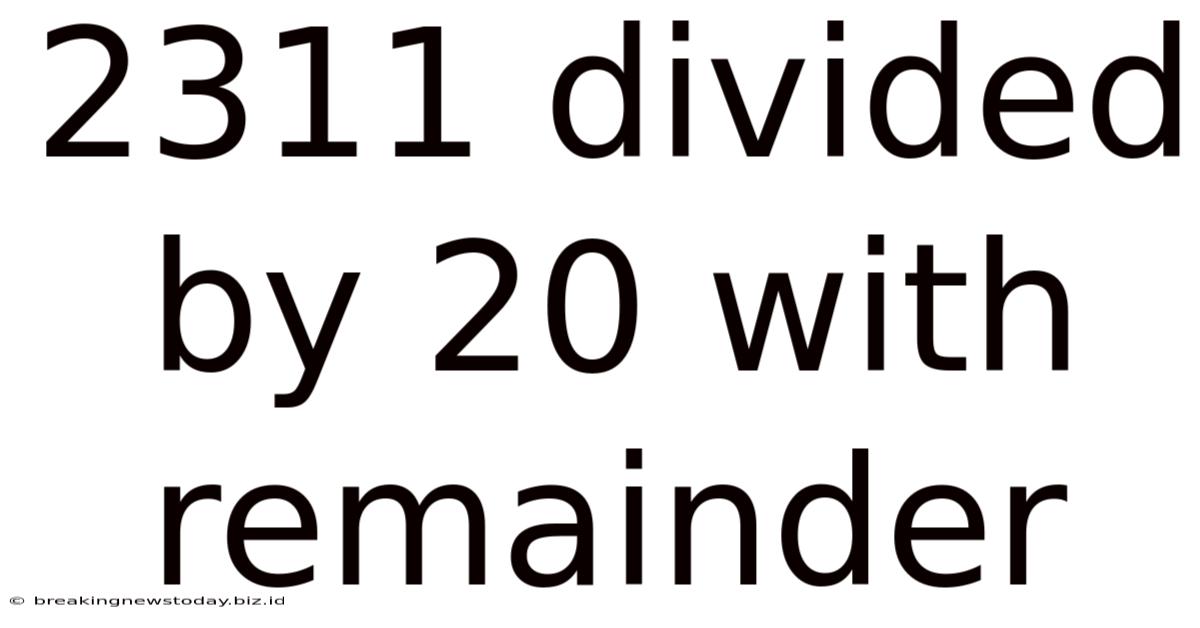
Table of Contents
2311 Divided by 20: A Deep Dive into Division with Remainders
Understanding division, particularly division with remainders, is a fundamental concept in mathematics with wide-ranging applications in various fields. This article will thoroughly explore the division of 2311 by 20, examining the process, interpreting the results, and highlighting the significance of remainders in practical contexts. We will delve into various methods of calculating the result and discuss the broader implications of this seemingly simple arithmetic operation.
Understanding Division and Remainders
Division is the process of splitting a quantity into equal parts. When we divide a number (the dividend) by another number (the divisor), we aim to find out how many times the divisor goes into the dividend completely. Sometimes, the dividend is not perfectly divisible by the divisor; in such cases, a remainder is left over. This remainder represents the portion of the dividend that cannot be equally distributed among the divisor.
The standard form for representing division with a remainder is:
Dividend = (Divisor × Quotient) + Remainder
where:
- Dividend: The number being divided (2311 in our case).
- Divisor: The number we are dividing by (20 in our case).
- Quotient: The number of times the divisor goes into the dividend completely.
- Remainder: The amount left over after the division.
Calculating 2311 Divided by 20
Let's now calculate 2311 divided by 20 using different methods:
Method 1: Long Division
Long division is a traditional method for performing division. Here's how we can solve 2311 divided by 20 using long division:
115
20 | 2311
-20
---
31
-20
---
111
-100
---
11
Therefore, 2311 divided by 20 is 115 with a remainder of 11.
Method 2: Repeated Subtraction
Repeated subtraction is a more intuitive method, especially for smaller numbers. We repeatedly subtract the divisor (20) from the dividend (2311) until we reach a number smaller than the divisor. The number of times we subtract is the quotient, and the remaining number is the remainder.
2311 - 20 = 2291 2291 - 20 = 2271 ...and so on, until we reach 11.
Counting the number of subtractions will yield the quotient, which is 115. The remaining number, 11, is the remainder. This method is less efficient for large numbers but demonstrates the underlying concept of division.
Method 3: Using a Calculator
Most calculators can easily handle division problems. Simply enter 2311 ÷ 20. The calculator will provide the quotient (115.55) which can be broken down into a quotient of 115 and a remainder which can be found by subtracting 115 * 20 from 2311 which also results in a remainder of 11.
Interpreting the Results: Quotient and Remainder
From our calculations, we have found that when 2311 is divided by 20:
- The quotient is 115. This represents the number of times 20 goes into 2311 completely.
- The remainder is 11. This is the amount left over after distributing 2311 equally into groups of 20.
Practical Applications of Remainders
The remainder in division problems is not just a leftover; it often carries significant meaning in practical situations:
1. Grouping and Distribution
Imagine you have 2311 apples and want to pack them into boxes containing 20 apples each. The quotient (115) tells you that you can fill 115 boxes completely. The remainder (11) means you will have 11 apples left over, which might require a separate, smaller box.
2. Time and Measurement
If you have a race that is 2311 meters long, and you want to break it into 20-meter segments, you can complete 115 segments (the quotient) and would have 11 meters left (the remainder) at the end of the race.
3. Modulo Operator in Programming
In computer programming, the modulo operator (%) provides the remainder of a division. This is extensively used in various applications such as:
- Determining even or odd numbers: A number is even if it leaves a remainder of 0 when divided by 2.
- Cyclic patterns: The modulo operator can help create repeating patterns or sequences.
- Hashing algorithms: Hashing algorithms often use modulo operations to map data into a smaller range of values.
4. Cyclic Calculations: Clock Arithmetic
Consider a 12-hour clock. If it's 10 o'clock and you add 15 hours, you wouldn't say it's 25 o'clock. Instead, you'd use the modulo operator. 10 + 15 = 25; 25 % 12 = 1. So, it would be 1 o'clock. This concept is crucial in understanding cyclical phenomena.
Expanding the Understanding: Different Bases and Applications
The principles of division with remainders extend beyond the decimal system. You can apply this to other number systems, such as binary, hexadecimal, etc. The core concept remains the same: splitting a quantity into equal parts and determining what remains.
In advanced mathematics, concepts such as modular arithmetic, which heavily relies on remainders, are used in cryptography, error correction codes, and other computationally intensive fields. Understanding the fundamentals of division with remainders, as illustrated through this example of 2311 divided by 20, forms a critical foundation for tackling these more advanced topics.
Conclusion: The Importance of Mastering Division with Remainders
Division with remainders is more than a simple arithmetic operation; it's a foundational concept that underpins many aspects of mathematics, computer science, and practical problem-solving. By thoroughly understanding the process, interpreting the results (both quotient and remainder), and recognizing its widespread applications, you develop a crucial skill set applicable in various contexts. The seemingly simple problem of 2311 divided by 20 serves as a potent illustration of this principle's power and versatility. Mastering this concept opens doors to a deeper understanding of numerical relationships and their practical implications.
Latest Posts
Latest Posts
-
Which Expression Shows The Total Area Of The Courtyard
Jun 04, 2025
-
Popular Topics For Madrigal Poetry Included
Jun 04, 2025
-
28 24 As A Product Of Two Factors
Jun 04, 2025
-
Consider The Graph Of Domestic Supply And Demand For Oil
Jun 04, 2025
-
Kathy Pays A Monthly Premium On Her Health Insurance Policy
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about 2311 Divided By 20 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.