24.94 Is 29 Percent Of What Number
Breaking News Today
Jun 03, 2025 · 4 min read
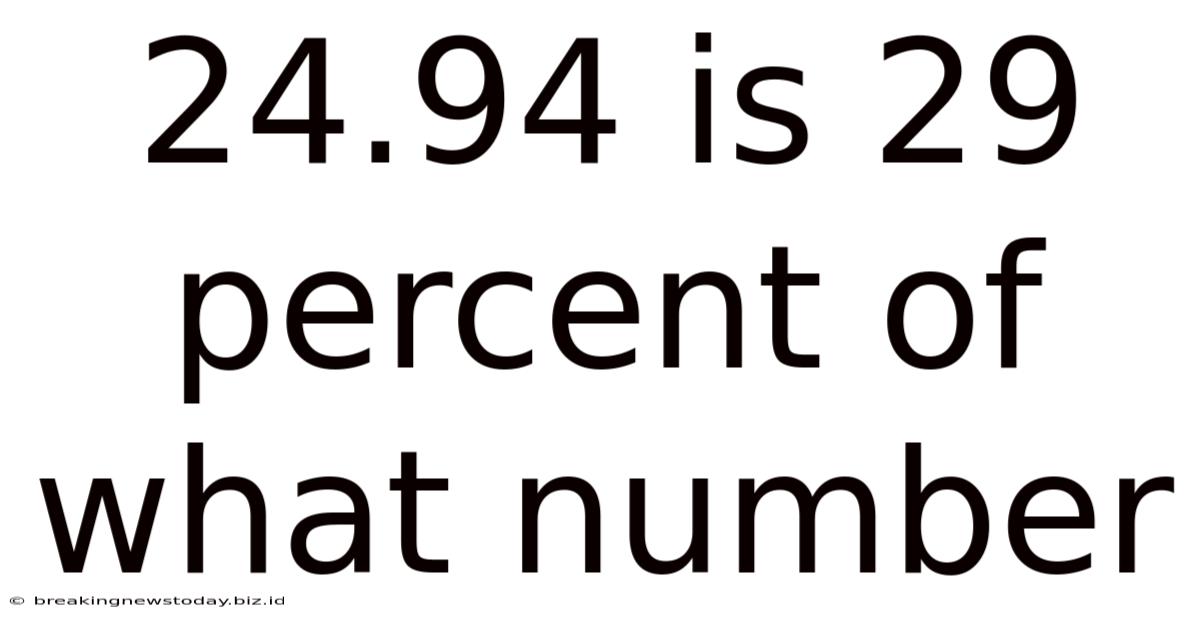
Table of Contents
Unraveling the Mystery: 24.94 is 29 Percent of What Number? A Deep Dive into Percentage Calculations
This article explores the solution to the problem "24.94 is 29 percent of what number?" We'll not only provide the answer but delve into the underlying mathematical principles, explore different methods of solving percentage problems, and offer practical applications to help you confidently tackle similar calculations in various real-world scenarios. We'll also touch upon the importance of percentage calculations in different fields and how to improve your problem-solving skills in this area.
Understanding Percentages: The Foundation
Before we jump into solving the specific problem, let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100". For example, 29% means 29/100 or 0.29. Understanding this fundamental concept is key to tackling percentage calculations effectively.
Method 1: The Algebraic Approach
This is the most common and arguably the most elegant method to solve percentage problems. We can express the problem as an algebraic equation:
- Let 'x' be the unknown number.
The problem states: 24.94 is 29% of x. We can translate this into an equation:
- 24.94 = 0.29 * x
To solve for 'x', we need to isolate it. We can do this by dividing both sides of the equation by 0.29:
- x = 24.94 / 0.29
Performing the division gives us:
- x = 86
Therefore, 24.94 is 29% of 86.
Method 2: Using Proportions
This method is particularly useful for visualizing the relationship between the parts and the whole. We can set up a proportion:
- 24.94 / x = 29 / 100
This proportion states that the ratio of 24.94 to the unknown number (x) is equal to the ratio of 29 to 100. To solve for 'x', we can cross-multiply:
-
24.94 * 100 = 29 * x
-
2494 = 29x
Now, divide both sides by 29:
-
x = 2494 / 29
-
x = 86
Again, we arrive at the same solution: 24.94 is 29% of 86.
Method 3: The Percentage Formula
The general formula for percentage calculations is:
- (Part / Whole) * 100 = Percentage
In our case, we know the "Part" (24.94) and the "Percentage" (29). We need to find the "Whole" (x). Let's rearrange the formula to solve for the Whole:
- Whole = (Part / Percentage) * 100
Substituting the known values:
-
Whole = (24.94 / 29) * 100
-
Whole = 0.86 * 100
-
Whole = 86
This method provides another pathway to the same solution.
Verifying the Solution
To ensure our answer is correct, we can perform a quick check:
- 29% of 86 = 0.29 * 86 = 24.94
The calculation confirms our result.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in our daily lives and across various professions. Here are some examples:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
- Retail: Determining sale prices, markups, and profit percentages.
- Science: Expressing experimental results, analyzing data, and calculating statistical significance.
- Statistics: Representing data as percentages in graphs, charts, and reports.
- Everyday Life: Calculating tips, understanding sales, and determining the nutritional content of food.
Improving Your Percentage Calculation Skills
Mastering percentage calculations requires practice and a solid understanding of the underlying concepts. Here are some tips for improvement:
- Practice regularly: Solve various percentage problems to build your confidence and speed.
- Understand the different methods: Familiarize yourself with the algebraic approach, proportions, and the percentage formula. Choose the method that best suits your understanding and the given problem.
- Use online resources: Numerous websites and apps offer practice problems and interactive tutorials.
- Break down complex problems: Divide complex percentage problems into smaller, manageable steps.
- Check your work: Always verify your solutions to ensure accuracy.
Beyond the Basics: More Complex Percentage Problems
While this article focused on a basic percentage problem, the principles discussed can be extended to more complex scenarios involving multiple percentages, consecutive discounts, or compound interest. These more advanced problems often require a deeper understanding of algebraic manipulation and the application of relevant formulas.
The Importance of Accuracy in Percentage Calculations
Accuracy is paramount when dealing with percentages, particularly in finance and other critical areas. A small error in calculation can have significant consequences. Always double-check your work and use appropriate tools or software to minimize the risk of errors.
Conclusion
This in-depth exploration of the problem "24.94 is 29 percent of what number?" not only provided the solution (86) but also highlighted the fundamental principles of percentage calculations. By understanding the different methods and practicing regularly, you can confidently tackle various percentage problems encountered in your daily life and professional pursuits. Remember the importance of accuracy and the wide range of applications for these seemingly simple calculations. Mastering percentage calculations will undoubtedly enhance your mathematical skills and problem-solving abilities across numerous disciplines.
Latest Posts
Latest Posts
-
For An Inverted Organization To Be Effective It Requires
Jun 04, 2025
-
Computerized Practice Management Software Does Not
Jun 04, 2025
-
The First Step In Reaming Conduit Is To
Jun 04, 2025
-
Stoichiometry Mystery Picture Answer Key Pdf
Jun 04, 2025
-
Which Statement Best Describes A Text With A Cause And Effect Structure
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about 24.94 Is 29 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.