28.71 Is What Percent Of 6.6
Breaking News Today
Jun 07, 2025 · 4 min read
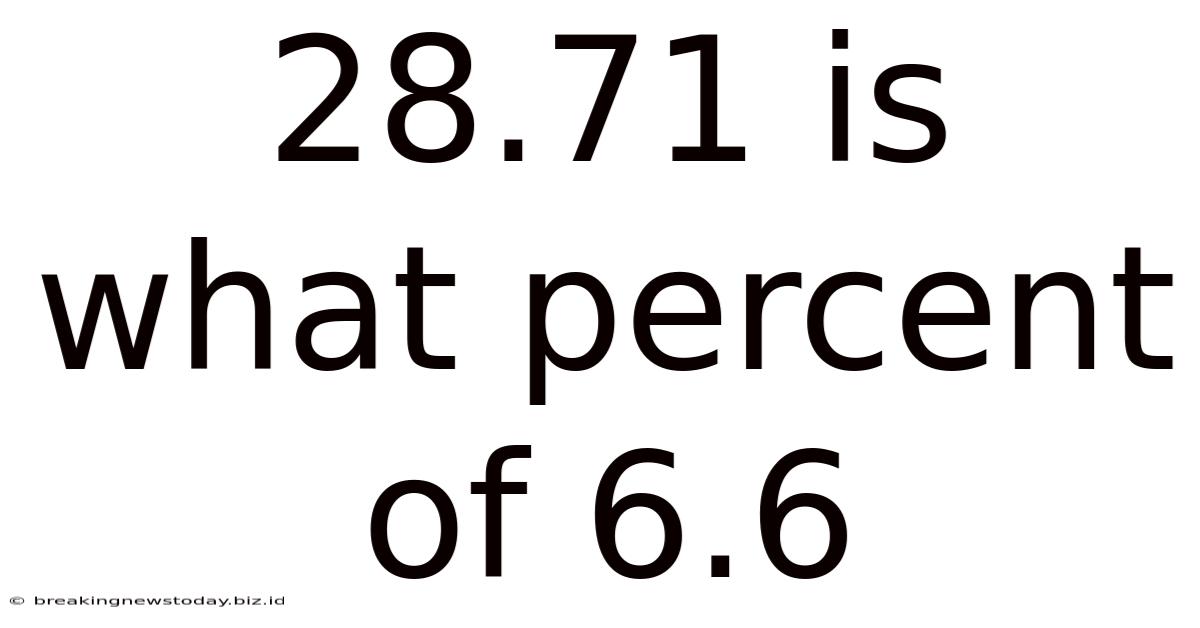
Table of Contents
28.71 is What Percent of 6.6? A Deep Dive into Percentage Calculations
This seemingly simple question, "28.71 is what percent of 6.6?", opens the door to a fascinating exploration of percentage calculations, their applications, and the underlying mathematical principles. While a calculator can quickly provide the answer, understanding the how behind the calculation is crucial for applying this knowledge to a wide range of scenarios in various fields. This article will not only answer the question but also provide a thorough understanding of percentage calculations, including practical applications and potential pitfalls.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" (from the Latin per centum). Percentages are used extensively in various contexts, including:
- Finance: Calculating interest rates, discounts, profit margins, and tax rates.
- Statistics: Representing data in charts and graphs, expressing probabilities, and analyzing survey results.
- Science: Measuring concentrations, expressing changes in quantities, and presenting experimental results.
- Everyday life: Calculating tips, understanding sales, and comparing prices.
Calculating Percentages: The Formula
The fundamental formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
Where:
- Part: Represents the value you want to express as a percentage of the whole.
- Whole: Represents the total value.
- Percentage: The resulting percentage.
Let's apply this to our initial question: "28.71 is what percent of 6.6?"
In this case:
- Part = 28.71
- Whole = 6.6
Therefore, the calculation is:
(28.71 / 6.6) * 100 = Percentage
Using a calculator, we find:
(28.71 / 6.6) * 100 ≈ 434.999 ≈ 435%
Therefore, 28.71 is approximately 435% of 6.6.
Interpreting the Result: A Percentage Greater Than 100%
The result, 435%, might seem counterintuitive at first glance. Percentages greater than 100% simply indicate that the "part" is larger than the "whole." This is perfectly valid mathematically and often occurs in real-world situations. For example:
- Financial Growth: If a company's revenue increases from $6.6 million to $28.71 million, the growth is 435%.
- Population Increase: If a town's population grows from 6,600 to 28,710, the increase is 435%.
- Data Expansion: If a dataset increases in size from 6.6 GB to 28.71 GB, the expansion is 435%.
Practical Applications and Examples
Let's explore some practical examples showcasing percentage calculations:
1. Calculating Discounts:
A store offers a 20% discount on an item priced at $50. What is the final price?
- Discount amount: ($50 * 20%) = $10
- Final price: $50 - $10 = $40
2. Calculating Tax:
A sales tax rate is 8%. What is the total cost of an item priced at $75?
- Tax amount: ($75 * 8%) = $6
- Total cost: $75 + $6 = $81
3. Calculating Interest:
An investment of $1000 earns 5% interest annually. What is the total value after one year?
- Interest earned: ($1000 * 5%) = $50
- Total value: $1000 + $50 = $1050
4. Analyzing Survey Results:
In a survey of 100 people, 30 prefer brand A, 45 prefer brand B, and 25 prefer brand C. What percentage of respondents prefer each brand?
- Brand A: (30 / 100) * 100% = 30%
- Brand B: (45 / 100) * 100% = 45%
- Brand C: (25 / 100) * 100% = 25%
Potential Pitfalls and Common Mistakes
While percentage calculations are relatively straightforward, several common mistakes can lead to inaccurate results:
- Incorrect order of operations: Always follow the order of operations (PEMDAS/BODMAS) to ensure accurate calculations.
- Confusion between percentage increase and percentage point increase: A change from 10% to 15% is a 5 percentage point increase but a 50% increase in percentage terms.
- Rounding errors: Be mindful of rounding errors, especially when dealing with multiple calculations. Round only at the final stage whenever possible.
- Incorrect interpretation of percentages: Always ensure a clear understanding of what the percentage represents relative to the whole.
Advanced Percentage Calculations: Working Backwards
Often, you might need to work backward from a percentage to find the original value. For example:
An item is discounted by 30%, and the final price is $70. What was the original price?
Let's denote the original price as 'x'. Then:
x - 0.30x = $70
0.70x = $70
x = $70 / 0.70 = $100
The original price was $100.
Conclusion: Mastering Percentages for Success
Understanding percentage calculations is a fundamental skill with wide-ranging applications. From everyday transactions to complex financial modeling, the ability to accurately calculate and interpret percentages is crucial. By grasping the underlying principles, practicing different scenarios, and being aware of potential pitfalls, you can confidently leverage this skill in numerous contexts, improving your analytical abilities and decision-making processes. This article has aimed to provide a comprehensive overview, equipping you with the knowledge and confidence to tackle percentage calculations with ease and precision. Remember to always double-check your calculations and clearly understand the context of the problem before making any conclusions. With practice, you'll become proficient in this essential mathematical tool.
Latest Posts
Latest Posts
-
Write Your Answer On A Separate Sheet Of Paper
Jun 07, 2025
-
Which Statute Generates Statistical Data Discrimination In Lending
Jun 07, 2025
-
A Business Paid 7000 To A Creditor
Jun 07, 2025
-
Which Of The Following Are True Statements Regarding Formal Counseling
Jun 07, 2025
-
Change The Layout Of The Workshop Participants
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 28.71 Is What Percent Of 6.6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.