2895 Divided By 229 With Remainder
Breaking News Today
Jun 01, 2025 · 4 min read
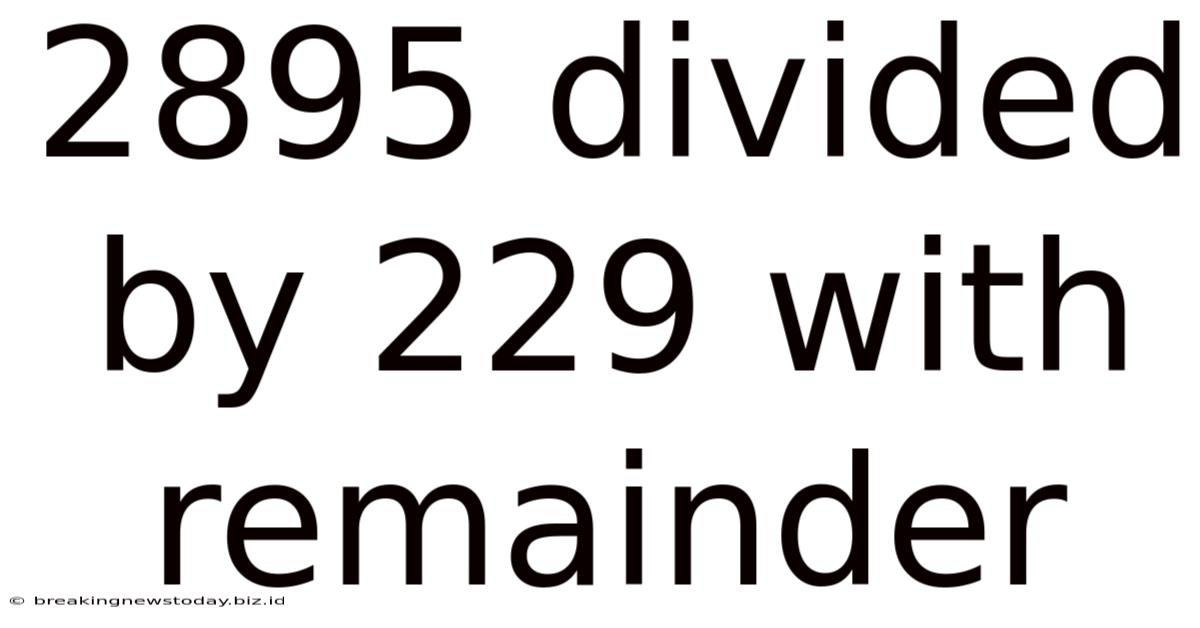
Table of Contents
2895 Divided by 229: A Deep Dive into Division with Remainders
Understanding division, especially division with remainders, is fundamental to mathematics. This seemingly simple operation forms the bedrock of more complex mathematical concepts and finds applications in various fields, from everyday calculations to advanced engineering. This article will comprehensively explore the division of 2895 by 229, examining the process, interpreting the results, and discussing the broader implications of division with remainders.
The Process of Division
Division is essentially the inverse operation of multiplication. When we say "2895 divided by 229," we're asking, "How many times does 229 fit into 2895?" The result is not always a whole number; often, we're left with a remainder – the portion that's left over after the division.
Let's perform the long division:
12
229 | 2895
-229
605
-458
147
The long division shows us that 229 goes into 2895 twelve times (12). However, there's a remainder of 147. This means that 2895 can be expressed as 12 times 229, plus an additional 147.
Interpreting the Results
The result of our division, 12 with a remainder of 147, can be interpreted in several ways:
-
Quotient and Remainder: The number 12 is called the quotient, representing the number of times the divisor (229) completely divides into the dividend (2895). The number 147 is the remainder, the amount left over.
-
Equation Form: The division can be expressed as an equation: 2895 = 229 * 12 + 147
-
Fractional Representation: The remainder can also be incorporated into a fraction. The result can be written as a mixed number: 12 147/229. This represents 12 whole units plus a fraction (147/229) of another unit.
Practical Applications of Division with Remainders
Division with remainders is far from a purely theoretical exercise. It appears in countless real-world scenarios:
-
Sharing: Imagine you have 2895 candies to distribute evenly among 229 children. Each child would receive 12 candies, and you'd have 147 candies left over.
-
Measurement: If you need to cut a 2895-meter-long rope into 229-meter sections, you'll get 12 full sections, with 147 meters remaining.
-
Programming: Remainders are crucial in computer programming for tasks such as determining if a number is even or odd (checking for a remainder of 0 when divided by 2), or creating patterns and cycles.
-
Scheduling: When scheduling tasks or resources, remainders can help determine how to distribute workloads or time efficiently.
-
Inventory Management: In inventory management, remainders can help track remaining stock and predict future needs.
Expanding on the Concept: Modular Arithmetic
The remainder in division is central to modular arithmetic, a branch of number theory with significant applications in cryptography and computer science. Modular arithmetic focuses on the remainder after division. The notation "a ≡ b (mod m)" means that a and b have the same remainder when divided by m. In our example, 2895 ≡ 147 (mod 229).
Applications of Modular Arithmetic:
-
Cryptography: Modular arithmetic is the foundation of many encryption algorithms used to secure online communications.
-
Hashing: Hashing algorithms use modular arithmetic to map large data sets into smaller, fixed-size values.
-
Error Detection: In data transmission, modular arithmetic can be used to detect errors in data.
-
Calendar Systems: Determining the day of the week for a given date frequently uses modular arithmetic.
Beyond the Basics: Exploring Different Division Methods
While long division is a standard method, other approaches exist for handling division problems:
-
Synthetic Division: A shortcut method for polynomial division, synthetic division is particularly useful for dividing polynomials by linear factors.
-
Calculator Use: Calculators can efficiently handle division, often providing both the quotient and the remainder. However, understanding the underlying principles remains crucial.
-
Estimation: Before performing the exact calculation, estimating the quotient can provide a valuable check on the reasonableness of the result.
Error Handling and Verification
It's always important to verify the results of division. One way to check is to use the equation form: Quotient * Divisor + Remainder = Dividend. In our case, 12 * 229 + 147 = 2748 + 147 = 2895. This confirms our result is correct.
Conclusion: The Importance of Remainders
The seemingly simple act of dividing 2895 by 229, resulting in a quotient of 12 and a remainder of 147, reveals the depth and breadth of mathematical concepts. Understanding division with remainders is not just about finding an answer; it's about grasping fundamental principles applicable across numerous fields. From everyday problem-solving to advanced mathematical applications, the remainder plays a critical role, highlighting the importance of appreciating the full picture of the division process. Mastering this concept forms a crucial stepping stone to further mathematical exploration and problem-solving abilities. The remainder isn't simply "leftover"; it holds significant meaning and functionality in various contexts.
Latest Posts
Latest Posts
-
Which Symbol Represents Front Windshield Defrosters
Jun 02, 2025
-
Sulfur Readily Forms The Following Monatomic Ion
Jun 02, 2025
-
Which Statement Best Describes How Igneous Rocks Are Formed
Jun 02, 2025
-
Match The Description Of The Murmur To The Valvular Lesion
Jun 02, 2025
-
87 5 Of What Number Is 49
Jun 02, 2025
Related Post
Thank you for visiting our website which covers about 2895 Divided By 229 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.