2x 2 4x 6x 2 9 6x 3
Breaking News Today
Jun 04, 2025 · 5 min read
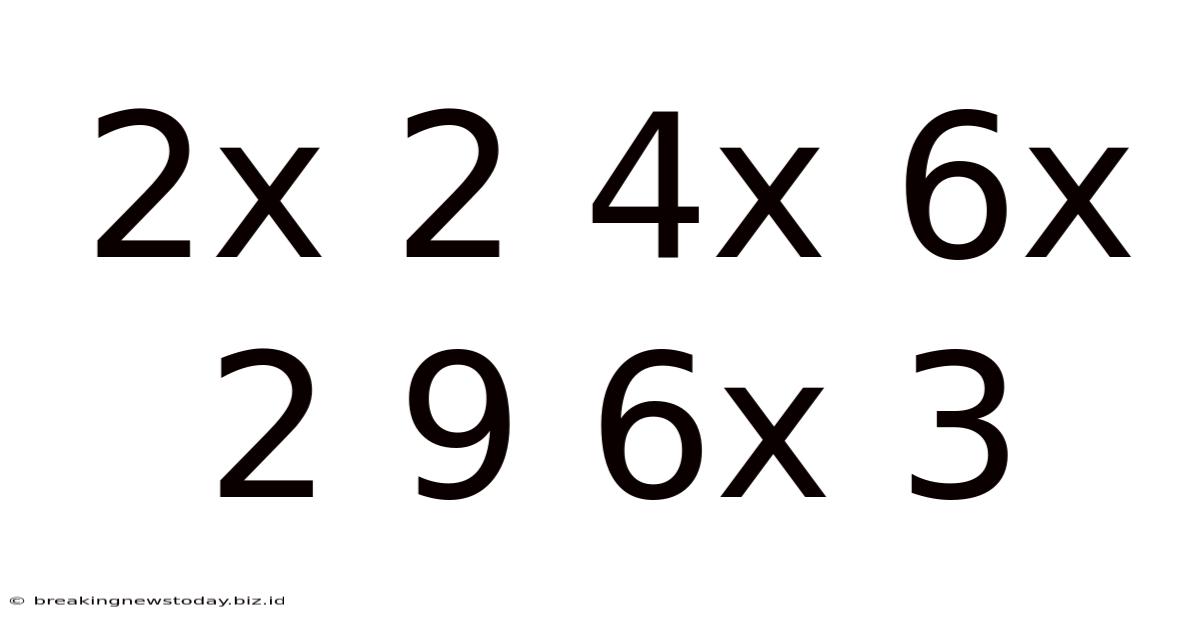
Table of Contents
Decoding the Sequence: Unveiling the Patterns and Possibilities of 2x2, 4x6x2, 9, 6x3
The seemingly random sequence "2x2, 4x6x2, 9, 6x3" presents a fascinating puzzle. At first glance, it appears chaotic, a jumble of numbers and multiplication signs. However, a closer examination reveals intriguing patterns and possibilities, opening doors to explorations in mathematics, coding, and even creative writing. This article delves deep into this sequence, exploring its potential meanings, uncovering hidden structures, and examining the myriad ways it can be interpreted.
The Initial Observation: A Mix of Operations and Numbers
The sequence "2x2, 4x6x2, 9, 6x3" immediately presents a challenge. We have a mix of single-digit numbers and expressions involving multiplication. This inherent ambiguity is key to unlocking multiple interpretations. The absence of clear mathematical operators between the expressions (no '+', '-', or '/') further complicates the straightforward interpretation. This lack of explicit structure necessitates a more creative, investigative approach.
Interpretation 1: A Sequence of Calculations
The most straightforward interpretation is to treat each element as a separate calculation. Let's break down each part individually:
- 2x2 = 4: A simple multiplication resulting in 4.
- 4x6x2 = 48: A straightforward multiplication chain.
- 9: A single-digit number, seemingly out of place initially.
- 6x3 = 18: Another simple multiplication.
This gives us a new sequence: 4, 48, 9, 18. At this point, the pattern isn't immediately obvious. However, we can start to look for relationships between these numbers. Are they multiples of a specific number? Do they share any common factors? Analyzing their prime factorization might reveal a hidden connection. Without additional context or information, this interpretation leaves many possibilities open.
Interpretation 2: A Coded Message
Could the sequence be a coded message? This interpretation requires us to consider a broader perspective. We need to think beyond simple mathematical calculations and consider alternative representations.
- Number System: Are we working in base 10? What if the sequence uses a different base?
- Cipher: Is a cipher or substitution code involved?
- Symbolic Representation: Could the numbers represent letters or other symbols based on a specific system?
For instance, a simple substitution cipher might assign each number to a letter of the alphabet (1=A, 2=B, etc.). However, without a key or more information, this interpretation remains highly speculative. More complex ciphers, like Vigenère ciphers or even more advanced encryption methods, become increasingly difficult to decipher without further clues.
Interpretation 3: A Pattern in Differences or Ratios
Another approach involves analyzing the differences or ratios between the results of the initial calculations (4, 48, 9, 18).
- Differences: The differences between consecutive numbers are 44, -39, -9. No clear pattern emerges from this approach.
- Ratios: The ratios between consecutive numbers are 12, 0.1875, 2. Again, no immediate pattern presents itself.
While these differences and ratios don't reveal an obvious pattern, they provide a starting point. More sophisticated mathematical analyses, including the study of sequence patterns and recursive relationships, might be needed to uncover a hidden structure. We might need to consider other mathematical operations like addition or subtraction between these results, or possibly even modular arithmetic.
Interpretation 4: A Recursive Sequence
Could this sequence be defined recursively? A recursive sequence is one where each term is defined based on previous terms. Let's explore this possibility. While we don't see an obvious recursive pattern in the initial calculations, we can investigate potential functions that could generate similar results. This might involve creating a custom function that uses the prior numbers and operations in the sequence to calculate the next number.
For example, a theoretical recursive function could be formulated, but without additional context, any formula would be purely speculative. The exploration of recursive sequences requires additional data points or clues to establish a definitive pattern.
Interpretation 5: A Programming Context
This sequence could also be part of a programming problem. The "x" symbol would naturally be interpreted as a multiplication operator. The sequence could be an input array or part of an algorithm. It might represent coordinate values, data points, or even represent instructions within a program. The interpretation would depend heavily on the context of the program itself. Is it related to image processing, game development, or some other computational task? The context would drastically alter the significance of the sequence.
Interpretation 6: A Creative Writing Prompt
Beyond mathematics and programming, the sequence could serve as an intriguing prompt for creative writing. The ambiguity and lack of a clear pattern allow for a multitude of interpretations.
- Mystery: The sequence could be a clue in a mystery novel, leading the protagonist to uncover a hidden message or location.
- Science Fiction: The sequence could represent alien coordinates, a code to unlock advanced technology, or a pattern observed in a strange natural phenomenon.
- Fantasy: The sequence could be a magical incantation, a pattern of runes, or part of a prophecy.
The creative freedom afforded by this ambiguous sequence is remarkable. It encourages imaginative leaps and opens pathways to exploring diverse narratives and symbolic interpretations.
Extending the Sequence: Predicting Future Terms
One common approach to analyzing sequences is trying to predict future terms. While no clear mathematical or logical pattern is immediately evident, we can speculate on potential extensions based on different interpretations. This is highly speculative, but it can stimulate further thought and analysis.
If we assume a purely numerical sequence (4, 48, 9, 18), we might look for patterns in the differences, ratios, or perhaps try to fit it to a known mathematical sequence type (arithmetic, geometric, Fibonacci, etc.). However, the erratic nature of this sequence makes this highly challenging without additional data or context.
Conclusion: The Power of Ambiguity
The sequence "2x2, 4x6x2, 9, 6x3" serves as a compelling example of the power of ambiguity. Its lack of a clearly defined pattern encourages a multifaceted approach, necessitating creativity, problem-solving skills, and the exploration of multiple fields like mathematics, programming, and creative writing. The seemingly simple sequence becomes a rich playground for investigation, highlighting the importance of context, critical thinking, and the diverse ways we can interpret information. Its inherent openness makes it a fantastic starting point for further investigation, and the possibilities for its interpretation are truly limitless. Further research, potentially involving more complex mathematical analysis and the consideration of additional context, could unveil further hidden patterns and meanings. The true power of this sequence lies in its capacity to spark curiosity and engage diverse approaches to problem-solving.
Latest Posts
Latest Posts
-
How Are The Two Passages Different
Jun 06, 2025
-
A Young Work Crew Is Trying To Quickly Finish
Jun 06, 2025
-
When Installing A Campus Backbone System Avoid The Use Of
Jun 06, 2025
-
Sydney Drew A Flow Chart To Illustrate The Nitrogen Cycle
Jun 06, 2025
-
Write 2 49 100 As A Decimal Number
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about 2x 2 4x 6x 2 9 6x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.