2x Y 3 4x 4y 8
Breaking News Today
Jun 04, 2025 · 5 min read
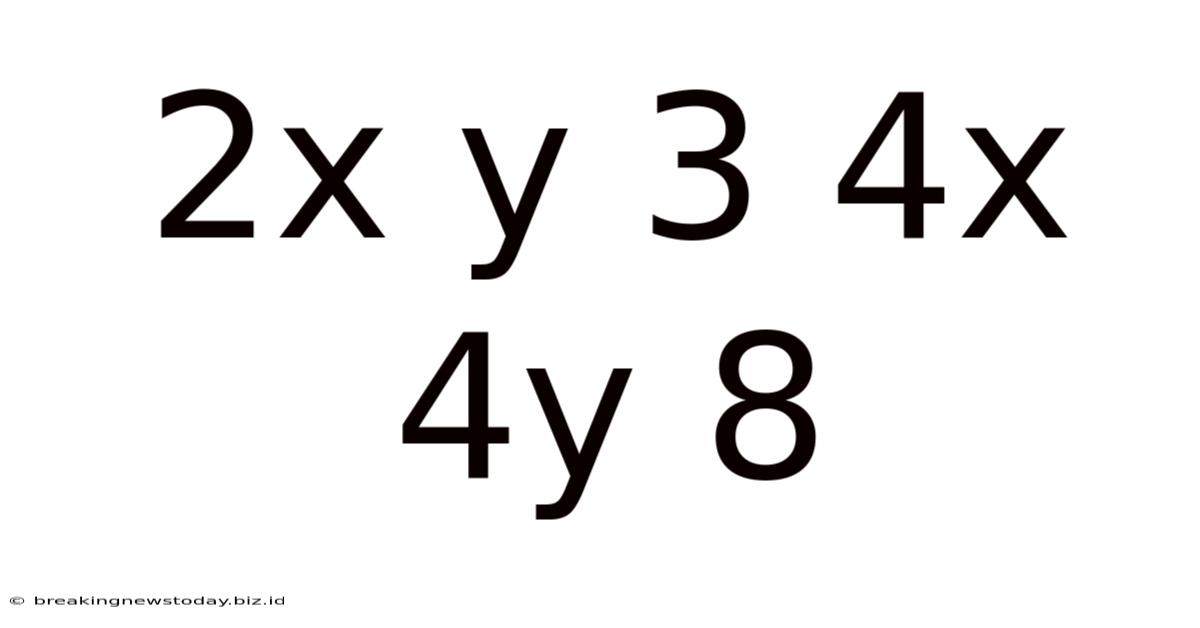
Table of Contents
Decoding the Mathematical Relationship: 2x y 3, 4x 4y 8
The seemingly simple equation, or rather, the presented pair of expressions: "2x y 3" and "4x 4y 8," presents a fascinating opportunity to explore various mathematical concepts. While not a formally written equation, the structure hints at a relationship between x and y, prompting us to investigate potential solutions and underlying principles. This exploration will delve into various approaches, from simple algebraic manipulation to more complex considerations of systems of equations and potential geometric interpretations.
Understanding the Problem: What are we looking for?
Before diving into solutions, it's crucial to define what we're trying to achieve. The expressions "2x y 3" and "4x 4y 8" aren't standard mathematical equations. They lack an equals sign (=), which signifies equivalence or equality. We can interpret them in several ways:
-
As inequalities: We could consider the expressions as inequalities, where one side is greater than, less than, or greater than or equal to the other. This would lead to a different kind of solution set.
-
As a system of equations (with assumed equality): We can assume an implied equality, interpreting them as a system of two equations with two unknowns:
- 2x + y = 3
- 4x + 4y = 8
-
As a representation of a functional relationship: We might consider whether 'y' is a function of 'x', or vice-versa. This will help us to analyze the behavior of 'y' with changing 'x' values.
This article will primarily focus on the second interpretation—treating the expressions as a system of simultaneous equations—because it offers a concrete and solvable problem.
Solving the System of Equations: Algebraic Approaches
Let's assume the expressions represent a system of linear equations:
- 2x + y = 3
- 4x + 4y = 8
We can solve this system using several algebraic techniques:
1. Elimination Method
This method involves manipulating the equations to eliminate one variable, allowing us to solve for the other. Notice that equation (2) is simply a multiple of equation (1):
- Dividing equation (2) by 4, we get: x + y = 2
Now we have a simplified system:
- 2x + y = 3
- x + y = 2
Subtracting equation (2) from equation (1):
(2x + y) - (x + y) = 3 - 2
This simplifies to: x = 1
Substituting x = 1 into either equation (1) or (2) allows us to solve for y. Using equation (2):
1 + y = 2
Therefore, y = 1
Solution: x = 1, y = 1
2. Substitution Method
This involves solving one equation for one variable and substituting the result into the other equation. Let's solve equation (1) for y:
y = 3 - 2x
Now substitute this expression for y into equation (2):
4x + 4(3 - 2x) = 8
Simplifying and solving for x:
4x + 12 - 8x = 8
-4x = -4
x = 1
Substituting x = 1 back into the expression for y:
y = 3 - 2(1) = 1
Solution: x = 1, y = 1
Both methods yield the same solution: x = 1 and y = 1. This confirms the consistency of the system.
Geometric Interpretation: Lines and Intersection
Linear equations can be represented graphically as straight lines. Each equation in our system represents a line on the Cartesian plane (x-y plane). The solution to the system (x = 1, y = 1) represents the point of intersection of these two lines. Since the second equation is a multiple of the first, both equations represent the same line. Therefore, they intersect at every point along that line.
Exploring Other Interpretations: Inequalities and Functional Relationships
Let's briefly touch on the other interpretations mentioned earlier.
Inequalities:
If we interpret "2x + y < 3" and "4x + 4y < 8", we're dealing with inequalities. Solving inequalities requires considering regions on the plane that satisfy the conditions. The solution set would be a region rather than a single point.
Functional Relationships:
We can also analyze the expressions as a functional relationship. If we solve for 'y' in each expression, we get:
- y = 3 - 2x
- y = 2 - x
Both represent linear functions. The first equation implies a steeper negative slope, while the second equation is less steep. Graphing these shows they are parallel lines which intersect only at the point (1, 1) which is consistent with our earlier solution set.
Expanding the Exploration: Adding Complexity
The initial problem, though simple, serves as a foundation for understanding more complex systems of equations. We can expand our exploration by considering:
-
Non-linear equations: Instead of linear equations, we could explore systems involving quadratic, cubic, or other non-linear functions. These systems can have multiple solutions or no solutions at all.
-
Systems with more variables: Expanding to three or more variables introduces increased complexity but also highlights the power of various matrix methods to find the solutions.
-
Applications in real-world problems: Systems of equations are fundamental to many fields, including physics, engineering, economics, and computer science. They model relationships between different variables, allowing us to solve for unknown quantities.
Conclusion: The Power of Simple Equations
While the initial expressions "2x y 3" and "4x 4y 8" appear uncomplicated, they provide a valuable entry point into the world of algebra and simultaneous equations. By exploring different approaches—algebraic manipulation, graphical representations, and alternative interpretations—we gain a deeper understanding of the relationships between variables and the power of mathematical tools to solve real-world problems. The solution, x=1 and y=1, while seemingly simple, unlocks a wealth of mathematical concepts and their practical applications. This exploration emphasizes the importance of clear problem definition and the versatility of different mathematical techniques in finding solutions. Remember, even seemingly basic problems can open doors to fascinating mathematical landscapes.
Latest Posts
Latest Posts
-
If A Stock Clerk Receives Six Shipments
Jun 05, 2025
-
The Graph Represents The Market For Breakfast Cereals
Jun 05, 2025
-
What Did The Detective Say To The Crook
Jun 05, 2025
-
Where Did The Granite Go On Saturday Night
Jun 05, 2025
-
What Makes The Figures In The Above Image Recognizably Korean
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 2x Y 3 4x 4y 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.