3/4 Has How Many 1/8 In It
Breaking News Today
Jun 05, 2025 · 5 min read
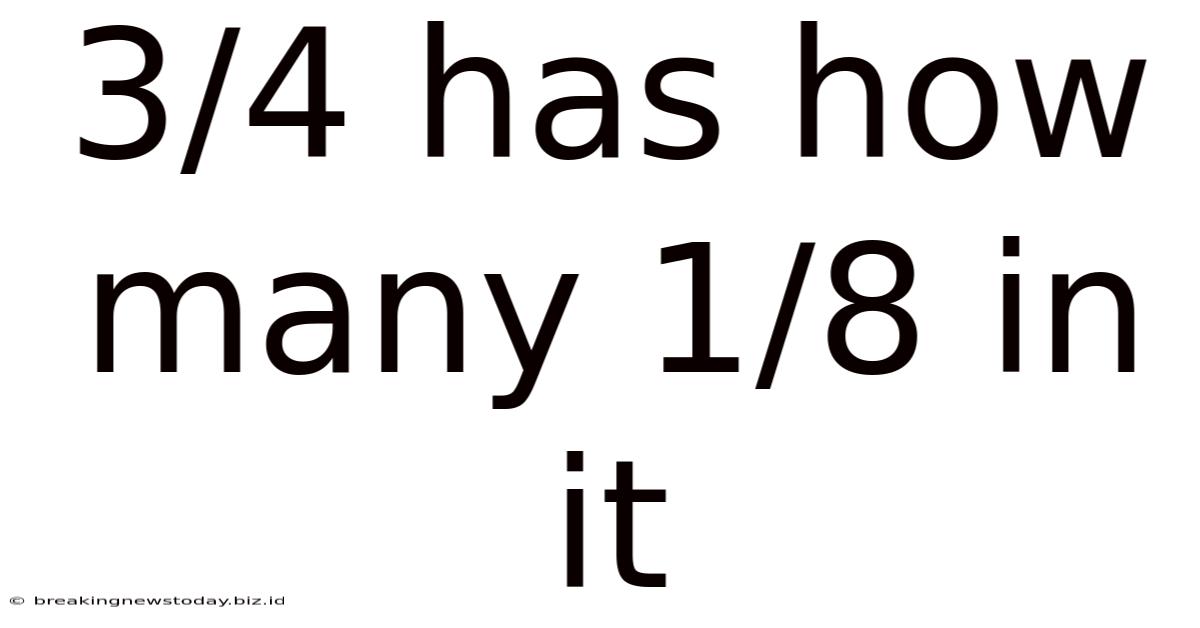
Table of Contents
3/4 Has How Many 1/8 in It? A Comprehensive Guide to Fraction Division
Understanding fractions is a cornerstone of mathematical literacy. This seemingly simple question, "3/4 has how many 1/8 in it?", unlocks a deeper understanding of fraction division, a concept crucial for various applications in everyday life and advanced mathematical studies. This comprehensive guide will not only answer the question directly but will also explore the underlying principles, offer multiple solution methods, and provide practical examples to solidify your understanding.
Understanding Fractions: A Quick Refresher
Before diving into the problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number indicates how many parts we have.
- Denominator: The bottom number indicates the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) signifies that we have three parts, and the denominator (4) signifies that the whole is divided into four equal parts.
Solving "How Many 1/8 are in 3/4?"
The core of this problem lies in understanding fraction division. We're essentially asking how many times 1/8 fits into 3/4. There are several ways to approach this:
Method 1: Direct Division
The most straightforward method involves dividing 3/4 by 1/8. Remember, dividing by a fraction is the same as multiplying by its reciprocal (flip the fraction).
- Rewrite the problem as a division: (3/4) ÷ (1/8)
- Invert the second fraction (find the reciprocal): (3/4) × (8/1)
- Multiply the numerators and the denominators: (3 × 8) / (4 × 1) = 24/4
- Simplify the fraction: 24/4 = 6
Therefore, there are 6 one-eighths (1/8) in three-quarters (3/4).
Method 2: Finding a Common Denominator
This method involves converting both fractions to have the same denominator before comparing them.
- Find a common denominator: The least common multiple (LCM) of 4 and 8 is 8.
- Convert 3/4 to have a denominator of 8: To change the denominator from 4 to 8, we multiply both the numerator and the denominator by 2: (3 × 2) / (4 × 2) = 6/8
- Compare the fractions: Now we have 6/8 and 1/8. How many times does 1/8 go into 6/8? The answer is simply the ratio of the numerators: 6 ÷ 1 = 6.
Again, we find that there are 6 one-eighths in three-quarters.
Method 3: Visual Representation
Visualizing the problem can be highly beneficial, especially for those who find abstract mathematical concepts challenging. Imagine a circle or a rectangle divided into 8 equal parts. Three-quarters of this shape would represent 6 out of the 8 parts (3/4 = 6/8). Clearly, there are six 1/8 sections within the 3/4 section.
Expanding the Understanding: Applications and Extensions
The ability to perform fraction division is not limited to simple mathematical problems. It's a vital skill with numerous real-world applications:
- Cooking and Baking: Recipes often require precise measurements. Understanding fractions helps in scaling recipes up or down accurately. For example, if a recipe calls for 3/4 cup of flour and you only have a 1/8 cup measuring cup, you'll need to measure six times to get the correct amount.
- Construction and Engineering: Precision is paramount in construction and engineering. Calculating material needs and measurements frequently involves fraction division.
- Sewing and Tailoring: Creating patterns and cutting fabric often necessitates precise fractional measurements.
- Data Analysis: Working with datasets often involves dealing with fractions and percentages, requiring a solid understanding of fraction manipulation.
- Financial Calculations: Budgeting, calculating interest rates, and other financial computations rely heavily on fractions and their operations.
Further Exploration: More Complex Fraction Problems
While the problem "3/4 has how many 1/8 in it?" is relatively simple, it provides a strong foundation for tackling more complex fraction problems. Here are a few examples to further challenge and enhance your understanding:
- Dividing fractions with larger numbers: Try solving problems like 15/16 ÷ 3/8 or 7/12 ÷ 5/24. The same principles of finding reciprocals and multiplying apply.
- Dividing mixed numbers: Mixed numbers contain both a whole number and a fraction (e.g., 2 1/3). Convert mixed numbers into improper fractions (a fraction where the numerator is larger than the denominator) before performing division. For instance, 2 1/3 becomes 7/3.
- Dividing fractions with different signs: Remember the rules for multiplying and dividing numbers with different signs: Positive divided by positive is positive; negative divided by positive is negative; and so on.
- Real-world problem solving: Create your own word problems involving fractions and apply the techniques learned to solve them.
Mastering Fraction Division: Tips and Strategies
Becoming proficient in fraction division requires practice and a structured approach. Here are some helpful strategies:
- Master the basics: Ensure a strong understanding of fraction simplification, finding common denominators, and converting between mixed numbers and improper fractions.
- Practice regularly: Work through numerous examples, starting with simpler problems and gradually progressing to more complex ones.
- Utilize visual aids: Draw diagrams and use visual representations to aid in understanding and problem-solving.
- Seek help when needed: Don't hesitate to ask for clarification or assistance from teachers, tutors, or online resources.
- Apply to real-world scenarios: Connect your learning to real-life situations to enhance understanding and retention.
Conclusion: Beyond the Numbers
The simple question, "3/4 has how many 1/8 in it?", serves as a gateway to a deeper comprehension of fraction division. Mastering this concept empowers you with a critical skill applicable in various aspects of life, from everyday tasks to complex calculations. By understanding the different methods, practicing regularly, and applying your knowledge to real-world problems, you'll build a strong foundation in fractions and confidently tackle more advanced mathematical concepts in the future. The journey of mastering fractions is a rewarding one, filled with the satisfaction of conquering mathematical challenges and gaining a deeper appreciation for the elegance and power of numbers. Remember, consistent practice and a strategic approach are key to achieving proficiency in this essential mathematical skill.
Latest Posts
Latest Posts
-
How Many Milligrams Are There In 4 5 Kilograms
Jun 07, 2025
-
How Fast Is The Relay Stick Moving Relative To Ingrid
Jun 07, 2025
-
12 1 8 As An Improper Fraction
Jun 07, 2025
-
When Sharing The Road With Construction Workers Be Prepared
Jun 07, 2025
-
Which Statement Best Summarizes A Central Idea In The Namesake
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Has How Many 1/8 In It . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.