3/4 Is 75 Of What Number
Breaking News Today
Jun 07, 2025 · 5 min read
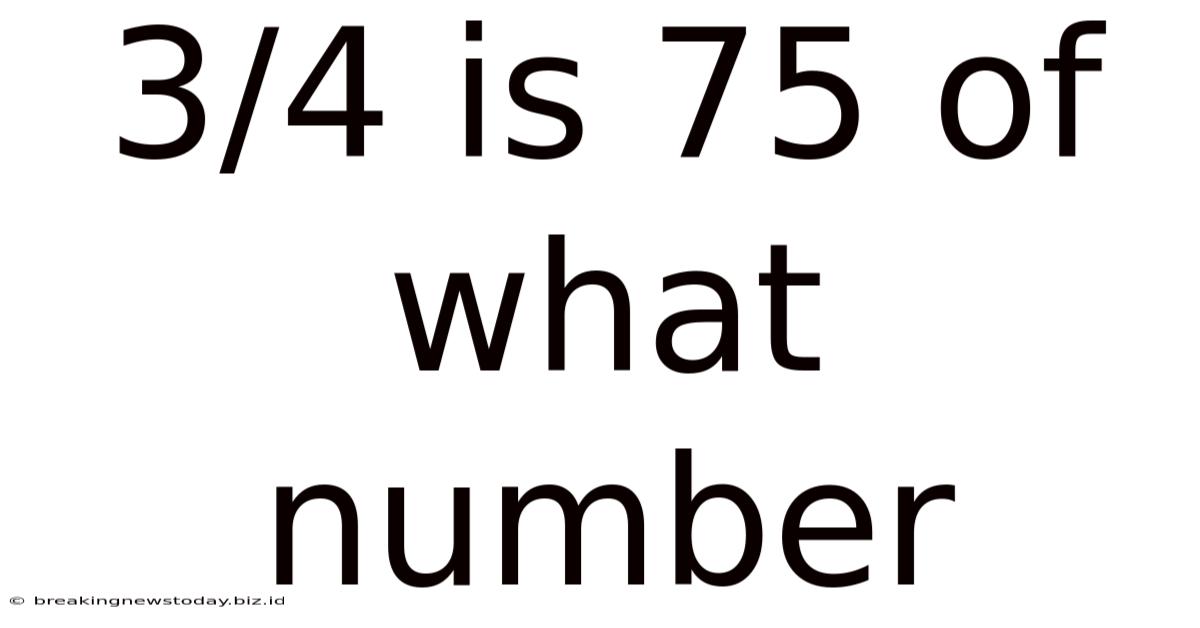
Table of Contents
3/4 is 75% of What Number: A Comprehensive Guide to Solving Percentage Problems
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article delves into the question, "3/4 is 75% of what number?", providing a step-by-step solution, exploring different approaches, and expanding on the broader concepts of percentages and their practical uses. We'll also look at how to solve similar problems and how to confidently tackle percentage calculations in various contexts.
Understanding the Problem: Deconstructing "3/4 is 75% of What Number?"
The core of the problem lies in the relationship between fractions, decimals, and percentages. We are given that 3/4 represents 75% of an unknown number. Our goal is to find that unknown number. This involves translating the problem into a mathematical equation that we can then solve.
Key Concepts:
- Fraction: A fraction represents a part of a whole. 3/4 means 3 parts out of 4 equal parts.
- Percentage: A percentage expresses a fraction as a proportion of 100. 75% means 75 out of 100, or 75/100.
- Equation: A mathematical statement that shows the equality of two expressions. We will construct an equation to represent the relationship between the given fraction, percentage, and the unknown number.
Method 1: Using Proportions
One of the most straightforward ways to solve this type of problem is by setting up a proportion. A proportion is an equation that states that two ratios are equal. We can represent the problem as:
3/4 = 75/100 = x/y
Where 'x' represents the part (3/4 or 75%) and 'y' is the whole number we're trying to find. Since we know that 75% is equivalent to 3/4, we can simplify the proportion:
3/4 = 75/100
To solve for 'y', we can cross-multiply:
3 * 100 = 4 * 75
300 = 300
This confirms the equivalence of 3/4 and 75%. However, this doesn't directly solve for the whole number 'y'. Let's adjust the proportion to reflect that 3/4 (or 75%) is a part of the whole number we're looking for. We can represent this as:
75/100 = 3/4 = x/y
Let's assume 'x' is 3 (representing the numerator of the fraction 3/4) and 'y' is the whole number we are trying to find. Then, the proportion becomes:
75/100 = 3/y
Cross-multiplying:
75y = 300
Solving for y:
y = 300/75
y = 4
Therefore, 3/4 is 75% of 4.
Method 2: Using Decimal Equivalents
We can also solve this problem using decimal equivalents. First, convert the fraction 3/4 to a decimal:
3/4 = 0.75
We know that 75% is also equivalent to 0.75 (75/100 = 0.75). We can now set up an equation:
0.75 * y = 3
Where 'y' is the unknown number. To solve for 'y', divide both sides by 0.75:
y = 3 / 0.75
y = 4
Again, we find that 3/4 is 75% of 4.
Method 3: Using Percentage Formula
The basic percentage formula is:
(Part / Whole) * 100 = Percentage
In our problem, the part is 3, the percentage is 75%, and the whole is the unknown number (let's call it 'x'). We can rearrange the formula to solve for 'x':
Part = (Percentage / 100) * Whole
3 = (75/100) * x
3 = 0.75x
x = 3 / 0.75
x = 4
Once again, we arrive at the solution: 3/4 is 75% of 4.
Expanding on Percentage Calculations: Practical Applications and Further Exploration
Understanding how to solve percentage problems is crucial for various real-world scenarios. Here are some examples:
- Calculating Discounts: If a store offers a 25% discount on an item priced at $80, you can calculate the discount amount and the final price using percentage calculations.
- Determining Tax Amounts: Sales tax is a percentage of the purchase price. Knowing how to calculate percentages helps determine the total cost of an item including tax.
- Analyzing Financial Data: Percentage changes in stock prices, interest rates, and other financial metrics are essential for investment decisions.
- Understanding Statistical Data: Percentages are commonly used to represent proportions in data analysis, such as survey results or demographic information.
- Calculating Grades and Scores: Many academic assessments use percentages to represent scores and grades.
Solving Similar Problems: A Step-by-Step Approach
Let's consider another example: "20% of what number is 10?"
Step 1: Identify the known values:
- Percentage: 20%
- Part: 10
Step 2: Set up the equation using the percentage formula:
Part = (Percentage/100) * Whole
10 = (20/100) * x
Step 3: Solve for the unknown ('x'):
10 = 0.2x
x = 10 / 0.2
x = 50
Therefore, 20% of 50 is 10.
Conclusion: Mastering Percentages for Everyday Success
This article has demonstrated multiple methods for solving percentage problems, specifically addressing the question, "3/4 is 75% of what number?". By understanding the relationship between fractions, decimals, and percentages, and applying the appropriate formulas and techniques, you can confidently tackle various percentage calculations in your daily life, academic pursuits, or professional endeavors. Remember to practice regularly to solidify your understanding and improve your problem-solving skills. The ability to work with percentages efficiently is a valuable asset that contributes significantly to success across numerous disciplines. From budgeting and financial planning to data analysis and scientific research, a solid grasp of percentages is indispensable.
Latest Posts
Latest Posts
-
Which Of The Following Options Describes The Spermatic Cord
Jun 07, 2025
-
Which Parts Of The Biodome Contain Carbon
Jun 07, 2025
-
If The Monopolist Charges A Single Price For Teddy Bears
Jun 07, 2025
-
Dr Adames Research Found That Athletes Perceived Concussions As
Jun 07, 2025
-
Which Answer Shows 0 00897 Written In Scientific Notation
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Is 75 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.