3/4 Of A Number Is 27 What's The Number
Breaking News Today
Jun 07, 2025 · 4 min read
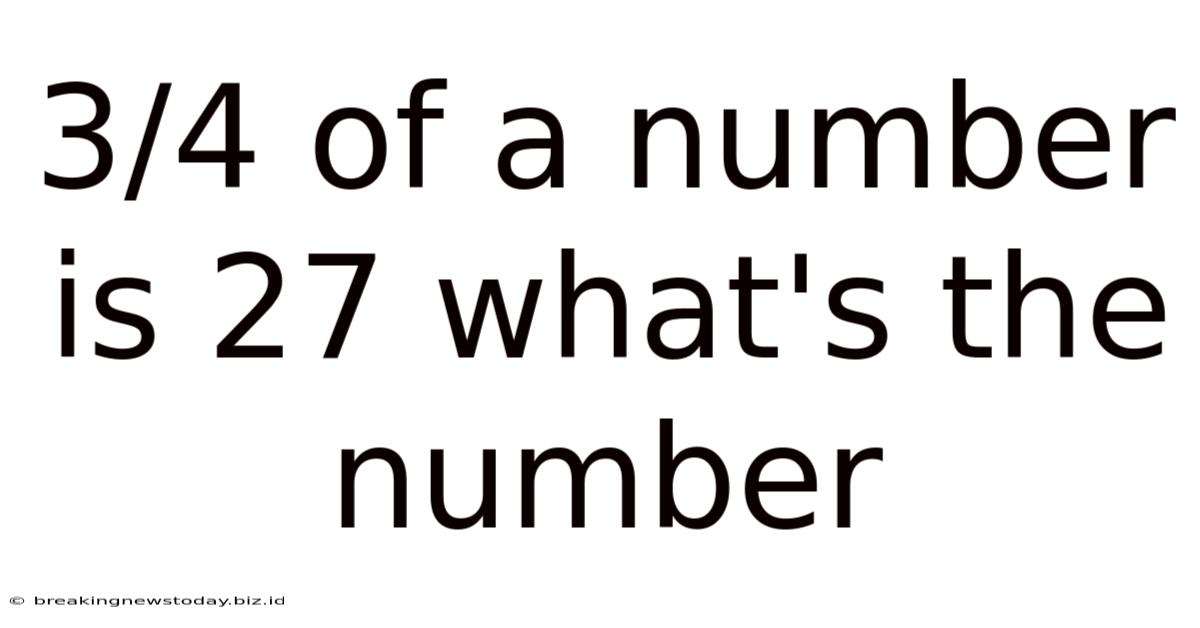
Table of Contents
3/4 of a Number is 27: What's the Number? A Deep Dive into Solving Algebraic Equations
This seemingly simple question, "3/4 of a number is 27, what's the number?", opens the door to a fascinating world of algebra and problem-solving. It's a perfect example of how mathematical concepts, even seemingly basic ones, can be applied to solve real-world problems. This article will not only provide the solution but also delve into the underlying principles, offering various approaches and exploring related concepts. We'll even look at how to extend this knowledge to tackle more complex problems.
Understanding the Problem: Deconstructing the Question
The core of the problem lies in translating the verbal description into a mathematical equation. The phrase "3/4 of a number" directly translates to (3/4) * x, where 'x' represents the unknown number we're trying to find. The statement "is 27" translates to an equals sign (=). Therefore, the complete equation becomes:
(3/4) * x = 27
This is a simple algebraic equation, and solving it involves manipulating the equation to isolate 'x' on one side.
Method 1: Solving Using Inverse Operations
The most straightforward method involves using inverse operations to isolate 'x'. Since 'x' is multiplied by 3/4, we can undo this multiplication by multiplying both sides of the equation by the reciprocal of 3/4, which is 4/3.
(4/3) * (3/4) * x = 27 * (4/3)
The (4/3) and (3/4) on the left side cancel each other out, simplifying the equation to:
x = 27 * (4/3)
Now, we simply perform the multiplication:
x = (27 * 4) / 3 = 108 / 3 = 36
Therefore, the number is 36.
Method 2: Solving Using Cross-Multiplication
Another approach is to use cross-multiplication, particularly helpful when dealing with fractions. We can rewrite the equation as a proportion:
3/4 = 27/x
Cross-multiplying gives us:
3 * x = 4 * 27
3x = 108
Dividing both sides by 3:
x = 108 / 3 = 36
Again, we arrive at the solution: x = 36.
Method 3: Solving Using Decimal Representation
We can also solve this by converting the fraction 3/4 to its decimal equivalent, which is 0.75. The equation then becomes:
0.75x = 27
Dividing both sides by 0.75:
x = 27 / 0.75 = 36
This method yields the same result: x = 36.
Verification: Checking Our Answer
It's crucial to always verify our solution. We can do this by substituting our answer (x = 36) back into the original equation:
(3/4) * 36 = 27
27 = 27
Since the equation holds true, our solution, x = 36, is correct.
Extending the Concept: More Complex Problems
The principles used to solve this simple problem can be extended to solve more complex algebraic equations. Let's consider a slightly more challenging scenario:
"2/5 of a number, increased by 10, is equal to 22. Find the number."
This translates to the equation:
(2/5)x + 10 = 22
To solve this, we first subtract 10 from both sides:
(2/5)x = 12
Then, we multiply both sides by 5/2:
x = 12 * (5/2) = 30
Therefore, the number is 30. This example demonstrates how the same fundamental principles – using inverse operations to isolate the variable – apply to more complex scenarios.
Real-World Applications: Where This Matters
Understanding how to solve these types of equations isn't just about passing a math test; it has practical applications in various fields:
- Finance: Calculating percentages, interest rates, discounts, and profit margins all involve solving similar equations.
- Engineering: Proportionality and scaling are crucial in engineering designs, often requiring the solving of algebraic equations.
- Science: Many scientific formulas and calculations involve solving for unknown variables, just like in this example.
- Everyday Life: From calculating tips to splitting bills, proportional reasoning is used frequently in daily life.
Expanding Your Knowledge: Further Exploration
This problem serves as a stepping stone to more advanced algebraic concepts. Consider exploring:
- Simultaneous Equations: Problems involving two or more unknown variables.
- Quadratic Equations: Equations involving squared variables (x²).
- Inequalities: Equations involving inequality symbols (<, >, ≤, ≥).
Mastering basic algebraic equations is the foundation for tackling more complex mathematical problems. The ability to translate word problems into mathematical equations is a vital skill in numerous fields.
Conclusion: The Power of Problem-Solving
The seemingly simple question, "3/4 of a number is 27, what's the number?", highlights the power of algebraic thinking. By understanding the underlying principles and applying various solution methods, we can not only find the answer (36) but also develop a deeper understanding of mathematical problem-solving. This skill is transferable to numerous contexts, making it a valuable asset in both academic and professional settings. Remember to practice regularly and explore more complex problems to solidify your understanding and enhance your problem-solving abilities. The more you practice, the more confident and proficient you'll become in tackling mathematical challenges.
Latest Posts
Latest Posts
-
Economists Pay Close Attention To The Unemployment Rate Because
Jun 07, 2025
-
Which Of The Following Statements Is True Of Xmpp
Jun 07, 2025
-
To Safeguard Against Hacking Practicing Situational Awareness Means
Jun 07, 2025
-
Listeners Usually Realize How Tense A Speaker Is
Jun 07, 2025
-
A Warning Alert Can Be Displayed On The Taser 10
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Of A Number Is 27 What's The Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.