3.7 Repeating As A Mixed Number
Breaking News Today
Jun 08, 2025 · 5 min read
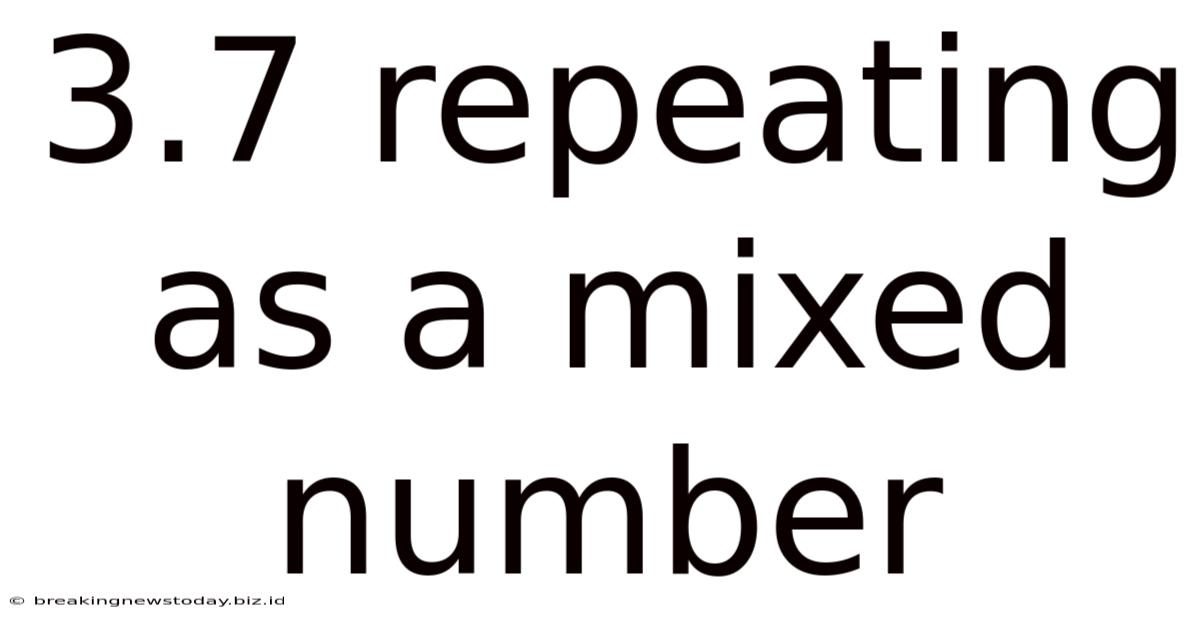
Table of Contents
Decoding 3.7 Repeating: A Deep Dive into Mixed Numbers and Decimal Conversions
The seemingly simple decimal 3.7 repeating (3.7777...) presents a fascinating challenge in mathematics, particularly when we aim to express it as a mixed number. This seemingly straightforward conversion requires a solid understanding of decimals, fractions, and the manipulation of algebraic equations. Let's embark on this journey, exploring the intricacies of this conversion and unveiling the underlying mathematical principles.
Understanding Repeating Decimals
Before diving into the conversion process, it's crucial to understand what a repeating decimal is. A repeating decimal is a decimal number where one or more digits repeat infinitely. In our case, 3.7 repeating (often written as 3.$\overline{7}$) signifies that the digit 7 repeats indefinitely. This contrasts with terminating decimals which have a finite number of digits after the decimal point.
The presence of a repeating decimal indicates a rational number – a number that can be expressed as a fraction of two integers. This is a fundamental concept that underpins our ability to convert 3.$\overline{7}$ into a mixed number.
The Conversion Process: Step-by-Step
Converting 3.$\overline{7}$ into a mixed number involves several steps. Let's break it down systematically:
1. Representing the Repeating Decimal Algebraically:
First, let's represent 3.$\overline{7}$ algebraically. Let x = 3.7777...
2. Multiplying to Shift the Decimal:
Next, we multiply both sides of the equation by 10 to shift the repeating part of the decimal:
10x = 37.7777...
3. Subtracting to Eliminate the Repeating Part:
Now, we subtract the original equation (x = 3.7777...) from the modified equation (10x = 37.7777...):
10x - x = 37.7777... - 3.7777...
This simplifies to:
9x = 34
4. Solving for x:
To solve for x, we divide both sides by 9:
x = 34/9
5. Converting the Improper Fraction to a Mixed Number:
The result, 34/9, is an improper fraction (the numerator is larger than the denominator). To express this as a mixed number, we perform long division:
34 ÷ 9 = 3 with a remainder of 7
Therefore, the mixed number equivalent of 34/9 is 3 ⁷⁄₉.
This confirms that 3.$\overline{7}$ is equal to the mixed number 3 ⁷⁄₉.
Verifying the Conversion: From Mixed Number to Decimal
To ensure the accuracy of our conversion, we can reverse the process. Let's convert the mixed number 3 ⁷⁄₉ back into a decimal:
First, convert the mixed number to an improper fraction:
3 ⁷⁄₉ = (3 * 9 + 7) / 9 = 34/9
Now, perform the division:
34 ÷ 9 = 3.7777...
This confirms that our conversion from 3.$\overline{7}$ to 3 ⁷⁄₉ is indeed correct.
The Significance of Rational Numbers and their Representations
This conversion exercise highlights the importance of understanding rational numbers and their diverse representations. The ability to seamlessly move between decimal, fractional, and mixed number forms is crucial for various mathematical applications, including:
- Algebra: Solving equations involving decimals often requires converting them to fractions for easier manipulation.
- Calculus: Understanding the nature of rational numbers is fundamental in calculus concepts such as limits and derivatives.
- Real-world applications: Many real-world problems involve measurements and quantities that necessitate conversions between different number forms.
Extending the Concept: More Complex Repeating Decimals
While 3.$\overline{7}$ is a relatively straightforward example, the same principles apply to more complex repeating decimals. For instance, consider a decimal like 1.2$\overline{34}$. The process remains similar, but requires multiplying by a higher power of 10 to align the repeating section for subtraction.
For 1.2$\overline{34}$, let x = 1.2343434...
- Multiply by 10: 10x = 12.343434...
- Multiply by 1000: 1000x = 1234.343434...
- Subtract 10x from 1000x: 990x = 1222
- Solve for x: x = 1222/990
- Simplify the fraction: x = 611/495
This improper fraction can then be converted to a mixed number. The key is to identify the repeating pattern and use appropriate powers of 10 to isolate and eliminate it.
Practical Applications and Real-World Examples
The conversion of repeating decimals to mixed numbers isn't just an academic exercise; it finds application in various real-world scenarios:
- Measurement and Engineering: Precise measurements often involve decimal values. Converting these to fractions can simplify calculations and enhance accuracy in engineering and construction projects.
- Finance and Accounting: Calculations involving monetary values frequently require the conversion of repeating decimals into fractions to avoid rounding errors and maintain precision.
- Computer Science: The representation of numbers in computer systems often relies on understanding the relationships between decimal, fraction, and binary forms.
Common Mistakes and How to Avoid Them
When converting repeating decimals to mixed numbers, several common mistakes can occur:
- Incorrectly identifying the repeating part: Carefully observe the decimal to accurately identify the repeating digits. A slight error here can lead to significant inaccuracies in the final result.
- Errors in algebraic manipulation: Accurate manipulation of equations is crucial. Double-check each step to ensure correctness.
- Mistakes during long division: Performing long division carefully is essential for accurately converting an improper fraction to a mixed number.
Conclusion: Mastering Decimal Conversions
Converting repeating decimals like 3.$\overline{7}$ into mixed numbers is a valuable skill that demonstrates a deeper understanding of number systems and algebraic manipulation. The ability to confidently navigate these conversions provides a strong foundation for tackling more complex mathematical problems and real-world applications. By mastering the systematic approach outlined in this article, one can confidently handle a wide range of decimal-to-fraction conversions, solidifying their mathematical skills and problem-solving capabilities. Remember to practice consistently and review the steps to improve accuracy and proficiency. The key is to understand the underlying principles and apply them methodically.
Latest Posts
Latest Posts
-
Describe The Initial Battle With The Monster
Jun 08, 2025
-
Which Would Most Likely Be Painted By A Renaissance Artist
Jun 08, 2025
-
Completa Las Oraciones De Forma L Gica Usando Pero O Sino
Jun 08, 2025
-
Bnw Is One Of Many Producers Of Luxury Wheelchairs
Jun 08, 2025
-
Diego Is In The Strange Situation With His Caregiver
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about 3.7 Repeating As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.