30 Tens - 3 Tens 3 Tenths
Breaking News Today
Jun 06, 2025 · 5 min read
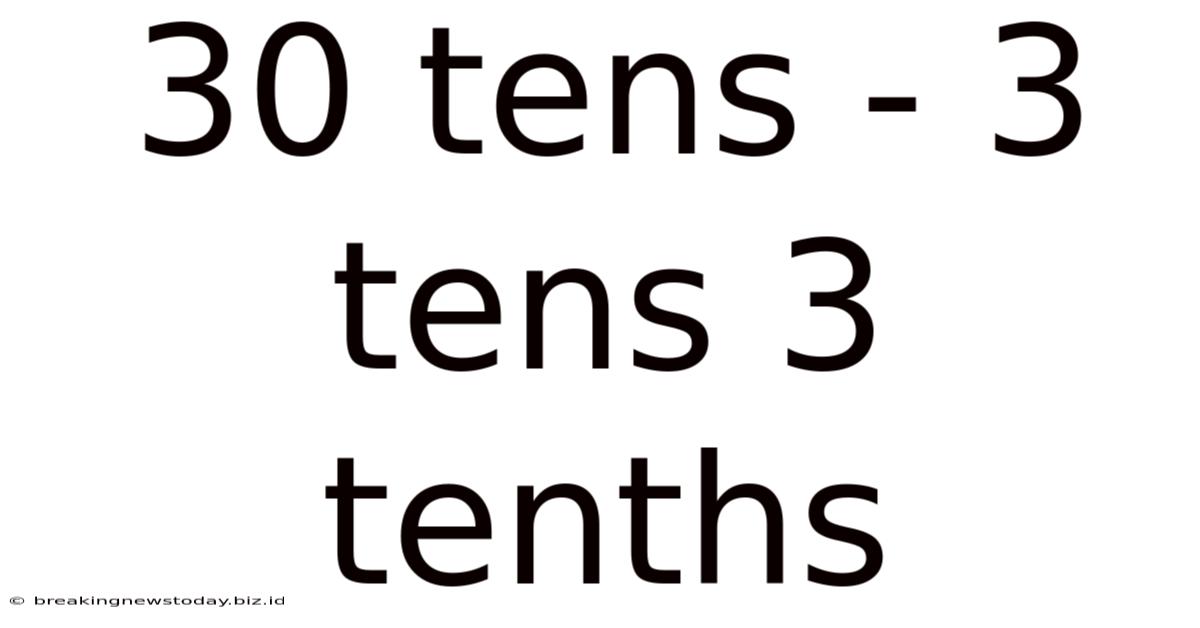
Table of Contents
Decoding 30 Tens - 3 Tens 3 Tenths: A Deep Dive into Decimal Place Value
Understanding place value is fundamental to mastering mathematics. This article delves into the seemingly simple yet often confusing concept illustrated by the expression "30 tens - 3 tens 3 tenths." We'll break down this expression step-by-step, explaining the underlying principles of place value in the decimal system, and exploring how this understanding translates to more complex mathematical operations. We will also touch upon the practical applications of this knowledge in various fields.
Understanding Place Value: The Foundation of Decimal Numbers
The decimal system, also known as the base-10 system, is the foundation of our number system. It's characterized by its use of ten digits (0-9) and its organization into place values based on powers of 10. Each place value represents a specific power of 10, starting from the rightmost digit which represents the ones place (10⁰ = 1). Moving to the left, we encounter the tens place (10¹ = 10), hundreds place (10² = 100), thousands place (10³ = 1000), and so on.
Conversely, moving to the right of the ones place, we enter the decimal portion of the number, representing fractions of 10. The first place to the right of the decimal point is the tenths place (10⁻¹ = 0.1), followed by the hundredths place (10⁻² = 0.01), thousandths place (10⁻³ = 0.001), and so forth. Each digit's position relative to the decimal point determines its value.
Breaking Down "30 Tens - 3 Tens 3 Tenths"
Let's analyze the expression "30 tens - 3 tens 3 tenths" systematically.
1. 30 Tens:
This represents 30 groups of ten, which is equivalent to 30 x 10 = 300. In the decimal system, this would be written as 300.
2. 3 Tens 3 Tenths:
This part of the expression is a little more nuanced. It represents:
- 3 Tens: This is equivalent to 3 x 10 = 30.
- 3 Tenths: This is equivalent to 3 x 0.1 = 0.3.
Therefore, "3 tens 3 tenths" combined equals 30 + 0.3 = 30.3
3. The Subtraction:
Now, we perform the subtraction: 30 tens - 3 tens 3 tenths = 300 - 30.3
Subtracting 30.3 from 300 gives us: 300 - 30.3 = 269.7
Visualizing Place Value: A Practical Approach
Understanding place value can be significantly enhanced through visualization. Imagine a number line, with the ones place at the center. To the left, you have the tens, hundreds, thousands, and so on, each representing an increasing power of 10. To the right, you have the tenths, hundredths, thousandths, each representing decreasing powers of 10 (or increasing negative powers). This visualization helps in grasping the relative value of each digit.
Another effective visualization technique is using base-10 blocks. Ones can be represented by small cubes, tens by rods of 10 cubes, hundreds by flats of 100 cubes, and so on. This concrete representation makes understanding the magnitude of numbers and their place value significantly easier.
Applications of Place Value Understanding
Understanding place value isn't just an academic exercise; it has wide-ranging practical applications in various fields:
-
Finance: Accurate calculations involving money rely heavily on place value. Understanding the difference between cents (hundredths) and dollars (ones) is crucial for managing personal finances, business accounting, and investment strategies. Errors in place value can lead to significant financial losses.
-
Engineering and Science: Precise measurements and calculations in engineering and scientific fields depend on a clear understanding of place value. For example, in physics, distinguishing between millimeters (thousandths of a meter) and meters is critical for accurate calculations. Incorrect placement of decimal points in scientific notations can lead to catastrophic consequences.
-
Data Analysis: Analyzing data involves interpreting numerical information, including decimals. Understanding place value is essential for accurate interpretations of data sets, particularly in fields such as statistics and epidemiology. For example, in a study about COVID-19 cases per million people, understanding the place value of millions is pivotal for correct analysis.
Expanding the Concept: Beyond Tens and Tenths
While our example focuses on tens and tenths, the principles of place value extend to all digits within a number, regardless of their magnitude. Consider the following examples:
- 5 hundreds 2 tens 7 ones: This is equivalent to 500 + 20 + 7 = 527.
- 1 thousand 3 hundreds 5 tens 9 ones: This translates to 1000 + 300 + 50 + 9 = 1359.
- 2 tenths 5 hundredths 8 thousandths: This equals 0.2 + 0.05 + 0.008 = 0.258.
By mastering the understanding of place value, we can easily convert these word descriptions into numerical representations and vice-versa.
Addressing Common Mistakes in Place Value
Common errors related to place value often stem from:
-
Decimal point placement: Misplacing the decimal point can drastically alter the value of a number. For instance, 3.5 is vastly different from 35. Care must be taken to ensure the decimal point is correctly positioned.
-
Zero placeholders: Understanding the significance of zeros as placeholders is crucial. For example, 105 is different from 15; the zero holds the tens place. Ignoring zero placeholders can lead to incorrect calculations.
-
Confusion between decimals and fractions: Although closely related, decimals and fractions represent the same concept, albeit in different forms. It's important to understand their inter-relationship to prevent errors in conversion and calculations.
Mastering Place Value: Tips and Tricks
-
Regular practice: Consistent practice with numerical problems is crucial for reinforcing the understanding of place value.
-
Use of manipulatives: Base-10 blocks or other manipulatives can help visualize place value and make learning more engaging.
-
Breaking down numbers: Break down complex numbers into their constituent place values to understand their individual components and total value.
-
Real-world applications: Relate the concept of place value to real-world scenarios to enhance understanding and retention.
Conclusion: The Importance of a Solid Foundation
Understanding place value is a cornerstone of mathematical proficiency. Its seemingly simple nature belies its crucial role in various mathematical operations and its widespread practical applications across different disciplines. By mastering the principles of place value, we build a solid foundation for tackling more complex mathematical challenges and for navigating the quantitative aspects of our world effectively. From managing personal finances to analyzing scientific data, a solid grasp of place value is an invaluable asset. The simple expression "30 tens - 3 tens 3 tenths" serves as a microcosm of the larger concept, underscoring the importance of accurate understanding and precise calculation. Through dedicated practice and a commitment to understanding the underlying principles, anyone can develop a mastery of place value and enhance their mathematical skills.
Latest Posts
Latest Posts
-
This Excerpt Best Shows That The Ancient Greeks Valued
Jun 07, 2025
-
According To Your Textbook Effective Listening Skills Are Important For
Jun 07, 2025
-
Aggregate Is A Form Of Plagiarism That Happens When
Jun 07, 2025
-
Pandora Loves Attention And Likes To Learn
Jun 07, 2025
-
A Translators Goal Is To Write A Text That
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 30 Tens - 3 Tens 3 Tenths . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.