378 Is What Percent Of 450
Breaking News Today
Jun 08, 2025 · 4 min read
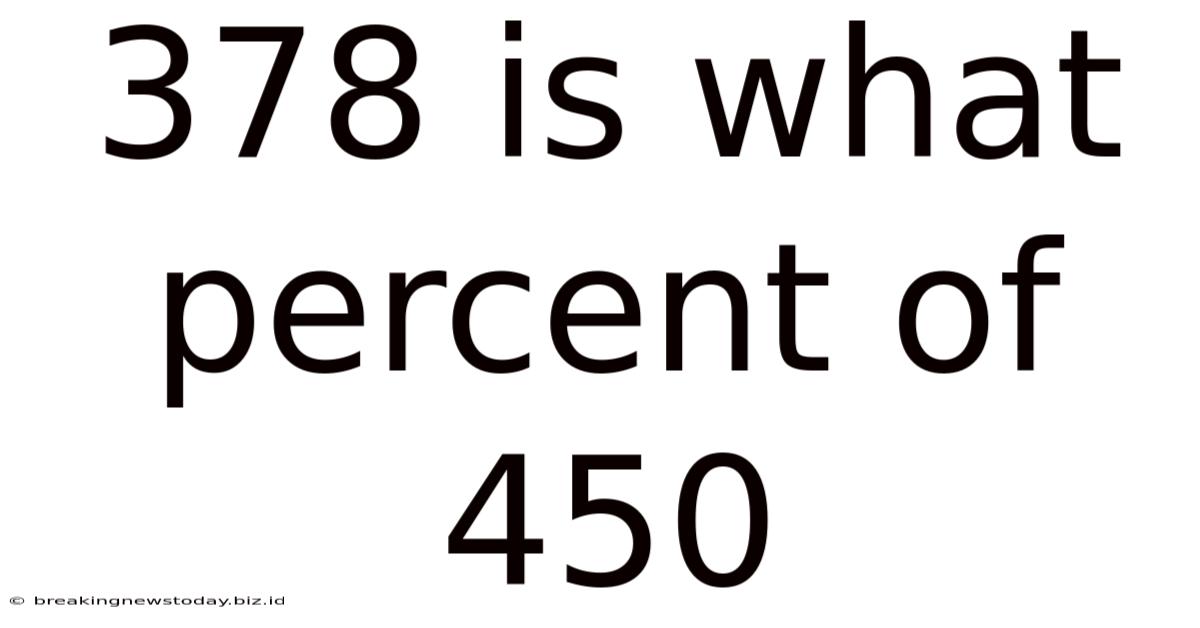
Table of Contents
378 is What Percent of 450? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex financial analysis. This article delves into the question, "378 is what percent of 450?", providing a step-by-step solution, exploring different calculation methods, and offering practical applications to solidify your understanding. We'll also cover related percentage problems and explore the broader context of percentage calculations within mathematics and real-world scenarios.
Understanding the Basics of Percentages
Before we dive into the specific problem, let's refresh our understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: Using the Percentage Formula
The most straightforward method to solve "378 is what percent of 450?" involves using the basic percentage formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 378
- Whole: 450
Substituting these values into the formula, we get:
(378 / 450) x 100% = Percentage
Calculating this:
0.84 x 100% = 84%
Therefore, 378 is 84% of 450.
Method 2: Using Proportions
Another approach involves setting up a proportion:
378/450 = x/100
Here, 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
378 * 100 = 450 * x
37800 = 450x
x = 37800 / 450
x = 84
Again, we find that 378 is 84% of 450.
Method 3: Using Decimal Conversion
This method involves converting the fraction 378/450 into a decimal and then multiplying by 100%:
- Divide 378 by 450: 378 ÷ 450 = 0.84
- Multiply the result by 100%: 0.84 x 100% = 84%
This confirms our previous findings: 378 is 84% of 450.
Practical Applications and Real-World Examples
The ability to calculate percentages is invaluable in numerous real-world situations. Here are a few examples:
-
Sales and Discounts: Imagine a store offering a discount. If an item is originally priced at $450 and is discounted to $378, you can use this percentage calculation to determine the discount percentage (84%). This helps shoppers understand the savings they're getting.
-
Grade Calculations: If you scored 378 points out of a possible 450 points on an exam, your percentage score would be 84%. This allows you to quickly assess your performance.
-
Financial Analysis: Percentages are crucial in analyzing financial statements. For example, you might calculate the percentage of revenue allocated to different departments or the percentage change in profit from one year to the next.
-
Surveys and Statistics: When analyzing survey results, percentages are often used to represent the proportion of respondents who chose a particular answer. For instance, if 378 out of 450 respondents favored a particular candidate, this represents an 84% approval rating.
-
Data Visualization: Percentages are frequently used in charts and graphs to visually represent proportions and trends within data sets.
Solving Related Percentage Problems
Let's explore some related percentage problems to further enhance your understanding:
1. Finding the Whole when given the Part and Percentage:
If 84% of a number is 378, what is the number?
We can set up the equation:
0.84 * x = 378
Solving for x:
x = 378 / 0.84
x = 450
Therefore, the number is 450.
2. Finding the Part when given the Whole and Percentage:
What is 84% of 450?
This can be calculated as:
0.84 * 450 = 378
3. Finding the Percentage Increase or Decrease:
If a value increases from 378 to 450, what is the percentage increase?
- Calculate the difference: 450 - 378 = 72
- Divide the difference by the original value: 72 / 378 ≈ 0.1905
- Multiply by 100%: 0.1905 x 100% ≈ 19.05%
Therefore, there's approximately a 19.05% increase.
Expanding Your Understanding: Advanced Percentage Concepts
While we've covered fundamental percentage calculations, there are more advanced concepts you can explore:
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest.
- Percentage Change: Understanding how to calculate percentage increases and decreases is vital for analyzing trends and making informed decisions.
- Percentage Points: These represent the actual numerical difference between two percentages, rather than a percentage change.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages is a crucial skill with widespread applications. By understanding the basic formula, various calculation methods, and practical applications, you can confidently tackle percentage problems in various contexts. The example of "378 is what percent of 450?" serves as a stepping stone to mastering more complex percentage calculations and applying this knowledge to real-world scenarios, from budgeting and financial planning to data analysis and interpretation. Remember to practice regularly and explore more advanced concepts to build a strong foundation in this important mathematical skill.
Latest Posts
Latest Posts
-
What Number Sentence Does This Model Show
Jun 08, 2025
-
Brake Fluid Expands And Contracts With Changes In Temperature
Jun 08, 2025
-
A Number Cube Numbered 1 6 Is Rolled Once
Jun 08, 2025
-
Which Sentence Is The Clearest Example Of Alliteration
Jun 08, 2025
-
What Is The Value Of The Underlined Digit 56
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about 378 Is What Percent Of 450 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.