4 Is Subtracted From The Square Of A Number
Breaking News Today
Jun 06, 2025 · 5 min read
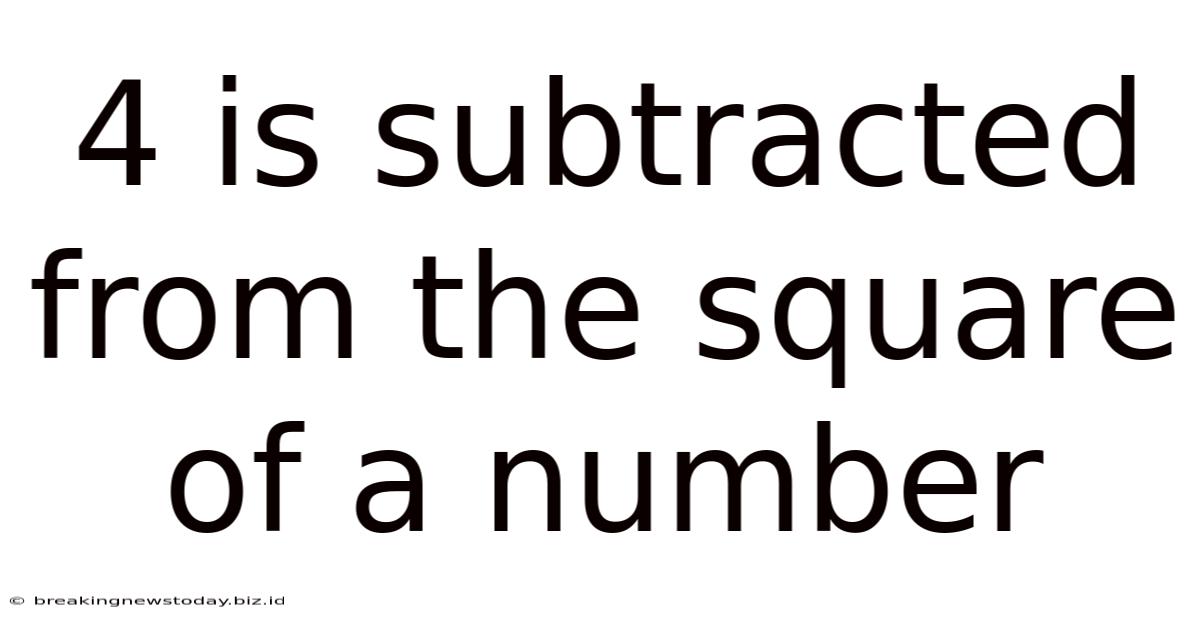
Table of Contents
4 is Subtracted from the Square of a Number: A Deep Dive into Quadratic Equations and Their Applications
The seemingly simple phrase, "4 is subtracted from the square of a number," opens a door to a fascinating world of mathematics, specifically quadratic equations. This seemingly basic statement holds within it the potential for exploring various mathematical concepts, problem-solving techniques, and even real-world applications. Let's delve into this seemingly simple problem and uncover its hidden depths.
Understanding the Core Concept: Quadratic Equations
The statement "4 is subtracted from the square of a number" can be translated directly into a mathematical equation. Let's represent the unknown number with the variable 'x'. The equation then becomes:
x² - 4 = 0
This is a classic example of a quadratic equation. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable is 2. The general form of a quadratic equation is:
ax² + bx + c = 0
where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. In our specific case, a = 1, b = 0, and c = -4.
Solving the Quadratic Equation: Factoring and the Quadratic Formula
There are several methods to solve quadratic equations. Let's explore two of the most common approaches: factoring and the quadratic formula.
Factoring
Factoring involves expressing the quadratic equation as a product of two simpler expressions. Our equation, x² - 4 = 0, is a difference of squares, which can be factored easily:
(x - 2)(x + 2) = 0
This factored form tells us that the equation is satisfied if either (x - 2) = 0 or (x + 2) = 0. Solving these simpler equations gives us the solutions:
- x = 2
- x = -2
Therefore, the two numbers whose squares, when 4 is subtracted, result in zero are 2 and -2.
The Quadratic Formula
The quadratic formula provides a general solution for any quadratic equation. It's derived from completing the square and is given by:
x = [-b ± √(b² - 4ac)] / 2a
Applying this formula to our equation (where a = 1, b = 0, and c = -4), we get:
x = [-0 ± √(0² - 4 * 1 * -4)] / (2 * 1) x = ± √16 / 2 x = ± 4 / 2 x = ± 2
Again, this confirms our solutions: x = 2 and x = -2.
Extending the Problem: When the Result is Not Zero
Let's make the problem more challenging. Instead of subtracting 4 from the square of a number and getting 0, let's say the result is a different number, say 'k'. The equation then becomes:
x² - 4 = k
This can be rearranged into a standard quadratic equation:
x² - 4 - k = 0
Now, 'k' can be any real number. The solutions will depend on the value of 'k'. We can use either factoring (if possible) or the quadratic formula to find the solutions for any given value of 'k'.
For example, if k = 5, the equation becomes:
x² - 9 = 0 (x - 3)(x + 3) = 0 x = 3 or x = -3
If k = -1, we have:
x² - 3 = 0 x = ±√3
The value of 'k' significantly impacts the nature of the solutions. The discriminant (b² - 4ac) within the quadratic formula determines the type of solutions:
- b² - 4ac > 0: Two distinct real solutions.
- b² - 4ac = 0: One real solution (a repeated root).
- b² - 4ac < 0: Two complex conjugate solutions (involving imaginary numbers).
Real-World Applications: Where Do Quadratic Equations Appear?
Quadratic equations are not just abstract mathematical concepts; they have numerous applications in various fields:
Physics: Projectile Motion
The trajectory of a projectile (like a ball thrown in the air) follows a parabolic path, which can be modeled using a quadratic equation. The equation describes the height of the projectile as a function of time, allowing us to determine the maximum height, the time of flight, and the range of the projectile.
Engineering: Bridge Design
The design of bridges often involves parabolic arches, which are described by quadratic equations. Engineers use quadratic equations to determine the structural integrity and stability of these arches.
Economics: Maximizing Profit
In business and economics, quadratic equations can be used to model profit functions. By finding the vertex of the parabola represented by the quadratic equation, businesses can determine the optimal production level to maximize their profit.
Computer Graphics: Creating Curves
Quadratic equations are fundamental in computer graphics for creating smooth curves and shapes. They are used in various algorithms for rendering and animation.
Advanced Concepts and Extensions
The simple problem of subtracting 4 from the square of a number can lead to exploration of more advanced mathematical concepts:
- Complex Numbers: As mentioned earlier, if the discriminant is negative, the solutions will involve complex numbers. This opens up a whole new branch of mathematics with applications in various fields, including electrical engineering and quantum mechanics.
- Graphing Quadratic Equations: Visualizing the quadratic equation on a graph reveals its parabolic shape. Analyzing the vertex, intercepts, and axis of symmetry provides further insights into the equation's behavior.
- Numerical Methods: For more complex quadratic equations that cannot be easily factored, numerical methods like the Newton-Raphson method can be employed to approximate the solutions.
Conclusion: A Simple Problem with Profound Implications
What began as a straightforward statement – "4 is subtracted from the square of a number" – has unveiled a rich tapestry of mathematical concepts and practical applications. From the fundamental principles of quadratic equations to their far-reaching implications in various fields, this seemingly simple problem serves as a gateway to a deeper understanding of mathematics and its power in solving real-world problems. By exploring this problem, we've touched upon factoring, the quadratic formula, the nature of solutions, and the diverse applications of quadratic equations. This exploration underscores the beauty and utility of mathematics, demonstrating how even simple beginnings can lead to profound discoveries. The continued exploration of such problems is essential for fostering critical thinking and problem-solving skills, crucial aspects of any scientific or technical endeavor.
Latest Posts
Latest Posts
-
Which Analogy Shows A Part To Whole Relationship
Jun 07, 2025
-
Which Of The Following Is True Compressed Urls
Jun 07, 2025
-
Which Statement Best Describes Hamlets Complexity In The Excerpt
Jun 07, 2025
-
Which Event Best Illustrates The Monsters Good Side
Jun 07, 2025
-
Getting A Credit Card Math Quiz
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 4 Is Subtracted From The Square Of A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.