4 Times The Sum Of X And 1/2
Breaking News Today
Jun 02, 2025 · 5 min read
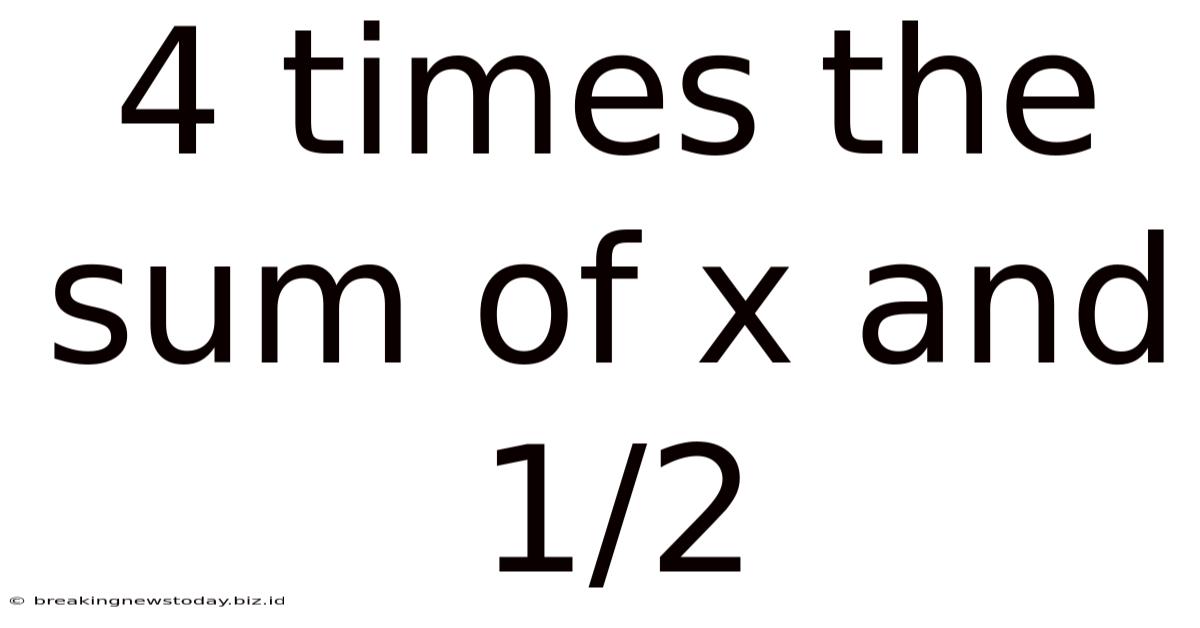
Table of Contents
4 Times the Sum of x and 1/2: A Deep Dive into Mathematical Expressions
This article explores the mathematical expression "4 times the sum of x and 1/2," dissecting its components, demonstrating its applications, and expanding on its relevance within broader mathematical concepts. We'll delve into various interpretations, potential complexities, and practical examples to provide a comprehensive understanding.
Understanding the Expression: Deconstructing the Components
The core of the expression lies in its layered structure. Let's break it down step-by-step:
-
x: This represents an unknown variable. Its value can be any real number (positive, negative, or zero). The beauty of algebra is its ability to represent unknown quantities symbolically. This allows us to create generalizable formulas and solve for specific instances.
-
1/2: This is a simple fraction, representing one-half or 0.5. It's a constant, meaning its value remains unchanged. The inclusion of a fraction adds an element of versatility to the expression, making it applicable to scenarios involving fractions or decimal values.
-
The Sum of x and 1/2: This phrase directs us to perform addition. We combine the variable x and the constant 1/2. This yields the expression (x + 1/2). Parentheses are crucial here, indicating that the addition must be performed before any subsequent multiplication. Order of operations (PEMDAS/BODMAS) dictates this sequence.
-
4 Times the Sum: Finally, we multiply the result of the addition by 4. This results in the complete expression: 4(x + 1/2). Again, the parentheses are vital. They ensure that the entire sum (x + 1/2) is multiplied by 4, not just the x.
Expanding the Expression: Algebraic Manipulation
The expression 4(x + 1/2) can be expanded using the distributive property of multiplication over addition. This property states that a(b + c) = ab + ac. Applying this to our expression, we get:
4(x + 1/2) = 4x + 4(1/2) = 4x + 2
This simplified form, 4x + 2, is equivalent to the original expression. Both forms are correct and can be used interchangeably, depending on the context and the desired approach to problem-solving. The expanded form (4x + 2) is often more convenient for further calculations and analysis.
Practical Applications: Real-World Scenarios
The expression "4 times the sum of x and 1/2" isn't just an abstract mathematical concept; it has practical applications in various real-world situations. Let's explore a few:
Example 1: Calculating Area
Imagine you're working with a rectangular area. Let's say the length of the rectangle is represented by x, and the width is consistently 1/2 unit more than the length. The total area of the rectangle is the length multiplied by the width. If you want to calculate four times the area, the expression becomes relevant.
- Length: x
- Width: x + 1/2
- Area: x(x + 1/2)
- Four Times the Area: 4 * x(x + 1/2) = 4x(x + 1/2) = 4x² + 2x
This scenario demonstrates how the expression can model real-world geometrical calculations.
Example 2: Calculating Costs
Let's say a particular item costs x dollars. A customer wants to buy four of these items, and each item has an additional 50-cent handling fee. The total cost can be represented using our expression:
- Cost per item: x + 0.5
- Total cost for four items: 4(x + 0.5) = 4x + 2
This example shows how the expression can be used to model financial calculations, such as total cost determination.
Example 3: Modeling Physical Quantities
In physics or engineering, the expression might represent a force, distance, or other physical quantities where a base value (x) is combined with a constant factor and then scaled by a multiplicative factor. For instance, it could describe the total displacement of an object undergoing four successive movements, with each movement consisting of a base displacement (x) and a fixed additional displacement (1/2 unit).
Solving for x: Different Approaches
Understanding how to solve for x given a specific value for the entire expression is crucial. Let's assume we know the expression equals a certain value, say, 10. Then, we have:
4(x + 1/2) = 10
We can solve for x using these steps:
- Distribute: 4x + 2 = 10
- Subtract 2 from both sides: 4x = 8
- Divide both sides by 4: x = 2
Therefore, if the entire expression equals 10, then x must equal 2. This process can be repeated for any given value of the expression. You can also use the simplified form, 4x + 2 = 10, directly to solve for x.
Beyond the Basics: Exploring Variations and Extensions
The core expression, 4(x + 1/2), provides a foundation for exploring more complex mathematical concepts. We can consider variations by:
-
Changing the constant: Instead of 1/2, we could use other constants like 1, 2, or even negative numbers. This would alter the expression's behavior and the resulting calculations.
-
Changing the multiplier: Instead of multiplying by 4, we could use any other number. This would again change the overall value of the expression.
-
Adding more variables: We could incorporate more variables into the expression, leading to more complex equations.
-
Introducing exponents: We could add exponents to the variables, leading to polynomial expressions.
These variations provide opportunities to delve deeper into algebraic manipulation, equation solving, and more advanced mathematical concepts.
Conclusion: The Significance of Simple Expressions
The expression "4 times the sum of x and 1/2" might appear simple at first glance. However, its layered structure reveals fundamental concepts in algebra, highlighting the importance of order of operations, the distributive property, and the ability to manipulate algebraic expressions. Its versatility in representing real-world scenarios showcases the power of mathematical modeling. By exploring this simple expression and its variations, we gain a stronger foundation in algebra and its applications across diverse fields. Understanding such fundamental expressions is crucial for tackling more complex mathematical problems in the future, whether in further mathematical study or applied problem solving in other disciplines. The ability to confidently manipulate and solve equations based on these simple expressions opens the door to a wide range of mathematical and scientific endeavors.
Latest Posts
Latest Posts
-
Which Statement About A Smoking Cessation Class Is True
Jun 04, 2025
-
The Polynomial X3 64 Is An Example Of A
Jun 04, 2025
-
Are People Influenced By What Others Say Michael Conducted
Jun 04, 2025
-
A Playwrights Use Of Meter Helps The Audience By
Jun 04, 2025
-
Which Row In The Table Labels The Diagram Correctly
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about 4 Times The Sum Of X And 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.