413 Divided By 2 With Remainder
Breaking News Today
Jun 07, 2025 · 5 min read
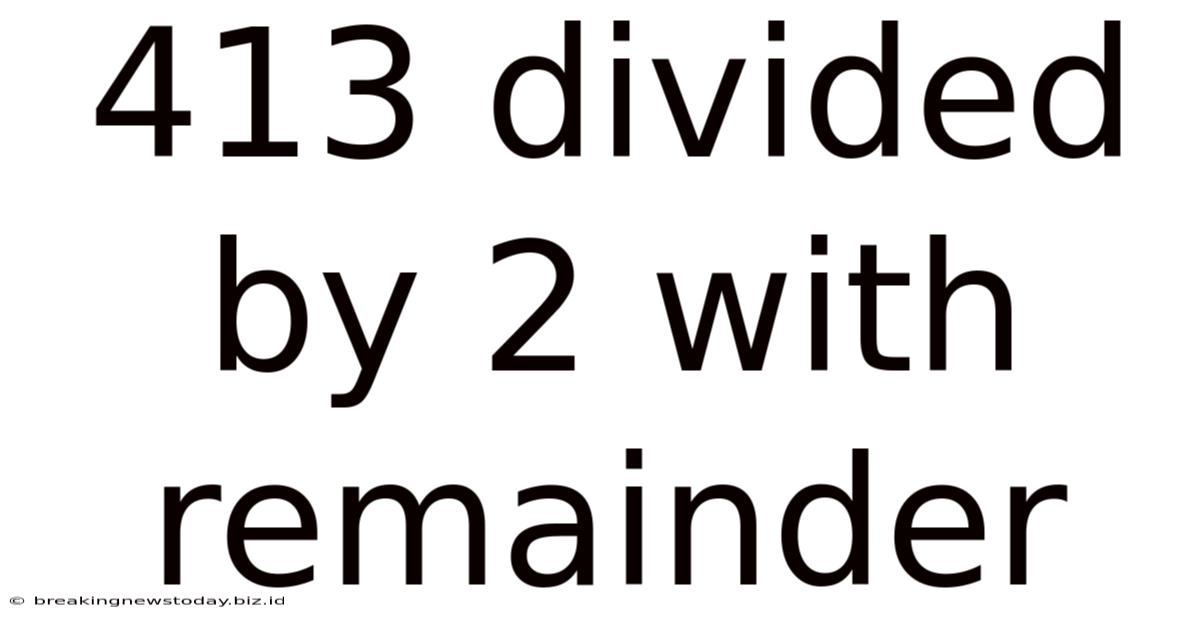
Table of Contents
413 Divided by 2 with Remainder: A Deep Dive into Division and Remainders
The seemingly simple question, "What is 413 divided by 2 with remainder?" opens a door to a fascinating exploration of fundamental mathematical concepts. While the answer itself is straightforward – using simple long division we get 206 with a remainder of 1 – delving deeper reveals crucial insights into division, remainders, their applications, and their significance in various fields. This article will explore this seemingly simple problem in depth, touching upon its theoretical underpinnings, practical applications, and connections to more advanced mathematical concepts.
Understanding Division and Remainders
Division is a fundamental arithmetic operation that involves splitting a quantity into equal parts. When we divide a number (the dividend) by another number (the divisor), we aim to find how many times the divisor fits into the dividend. The result is called the quotient. However, not all divisions result in a whole number quotient. When the dividend is not perfectly divisible by the divisor, we have a remainder – the amount left over after the division.
In the case of 413 divided by 2, we can represent this mathematically as:
413 ÷ 2 = 206 R 1
This means that 2 goes into 413 a total of 206 times, with 1 left over. The 206 is the quotient, and the 1 is the remainder.
The Importance of Remainders
Remainders aren't simply "leftovers"; they provide crucial information. They indicate that the division isn't exact, signifying an important property of the dividend and divisor. The remainder holds significance in various contexts:
-
Parity: Remainders when dividing by 2 are particularly important in determining the parity of a number (whether it's even or odd). A remainder of 0 signifies an even number, while a remainder of 1 indicates an odd number. This seemingly simple concept forms the basis of many more complex mathematical ideas.
-
Modular Arithmetic: Remainders are central to modular arithmetic, a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value (the modulus). Clock arithmetic is a familiar example; adding 14 hours to 3 pm gives us 5 pm (17 hours, which is 17 mod 12 = 5). The remainder after division by the modulus is the key element. This has wide-ranging applications in cryptography and computer science.
-
Data Structures and Algorithms: Remainders play a vital role in algorithms like hashing, where data is distributed across a hash table using a modulo operation to determine the index where a data element is stored. Efficient data retrieval depends on the properties of the remainders generated.
-
Real-World Applications: Consider distributing 413 candies equally among 2 children. Each child receives 206 candies, and there's 1 candy left over. The remainder helps us understand the distribution and address the leftover item. Similar scenarios exist in numerous applications where equal distribution is important, like resource allocation or task assignment.
Methods for Finding the Remainder
Several methods can be used to find the remainder when dividing 413 by 2:
1. Long Division: The traditional method of long division provides a systematic way to determine the quotient and remainder. This involves dividing the dividend (413) by the divisor (2) sequentially, step by step.
2. Short Division: A simplified version of long division, useful for smaller numbers and divisions by single-digit numbers.
3. Modular Arithmetic: This approach uses the modulo operator (%), which directly provides the remainder after division. In programming languages, this is often represented as the "%" symbol. In this case, 413 % 2 = 1.
Extending the Concept: Beyond 413 and 2
The principles we've explored using the example of 413 divided by 2 are applicable to any division problem. Understanding how to find the quotient and remainder is essential across various mathematical contexts. Let's consider some generalizations:
-
Dividing by Larger Numbers: The process remains the same, regardless of the size of the divisor. We can use long division or modular arithmetic to find the quotient and remainder for any division problem. For instance, 12345 divided by 17 would involve a more extensive long division process, but the core principle remains the same.
-
Dividing by Zero: It's crucial to remember that division by zero is undefined. There's no valid remainder when dividing by zero. This is a fundamental concept in mathematics.
-
Negative Numbers: When dealing with negative numbers, the sign of the remainder will depend on the signs of the dividend and divisor. For instance, -413 divided by 2 would result in a quotient of -206 and a remainder of -1 (or, alternatively, a quotient of -207 and a remainder of 1).
The Remainder Theorem and its Implications
The remainder theorem is a cornerstone of algebra. It states that when a polynomial is divided by a linear expression (x - a), the remainder is equal to the value of the polynomial when x = a. While this might seem unrelated to our simple division problem, it showcases a deeper connection between division and polynomial algebra. The remainder theorem is widely used in factoring polynomials, finding roots, and solving equations.
Applications in Computer Science
The concept of remainders is fundamental in computer science. It underpins numerous algorithms and data structures.
-
Hashing: Remainders are used to determine the location of data elements in hash tables, leading to efficient data retrieval.
-
Cryptography: Modular arithmetic, based on remainders, plays a critical role in modern encryption algorithms, ensuring the security of sensitive information.
-
Random Number Generation: Remainders are often used in pseudo-random number generators, producing sequences of numbers that appear random but are deterministic.
-
Error Detection and Correction: Remainders are utilized in error detection and correction codes, ensuring data integrity during transmission.
Conclusion: The Unassuming Power of Remainders
The seemingly trivial question of 413 divided by 2 with remainder reveals a rich tapestry of mathematical concepts. From the simple distinction between even and odd numbers to the complexities of modular arithmetic and its applications in advanced fields, the remainder emerges as a powerful and fundamental tool. Its significance extends beyond elementary arithmetic, playing a pivotal role in areas like computer science, cryptography, and abstract algebra. The next time you encounter a division problem, remember that the remainder holds more than just leftover value—it holds the key to deeper mathematical understanding and far-reaching practical applications. Understanding remainders strengthens our foundational mathematical skills and enhances our ability to tackle more complex computational challenges.
Latest Posts
Latest Posts
-
Picture Communication Is Easy For Naive Communication Partners To Understand
Jun 08, 2025
-
What Does The Imagery In The Passage Show About Doodle
Jun 08, 2025
-
Which Phrase From The Excerpt Best Supports A Pessimistic Tone
Jun 08, 2025
-
Write A Conjecture That Relates The Result Of The Process
Jun 08, 2025
-
Which Sentence Requires The Use Of A Citation
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about 413 Divided By 2 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.