421 Divided By 27 With Remainder
Breaking News Today
Jun 04, 2025 · 6 min read
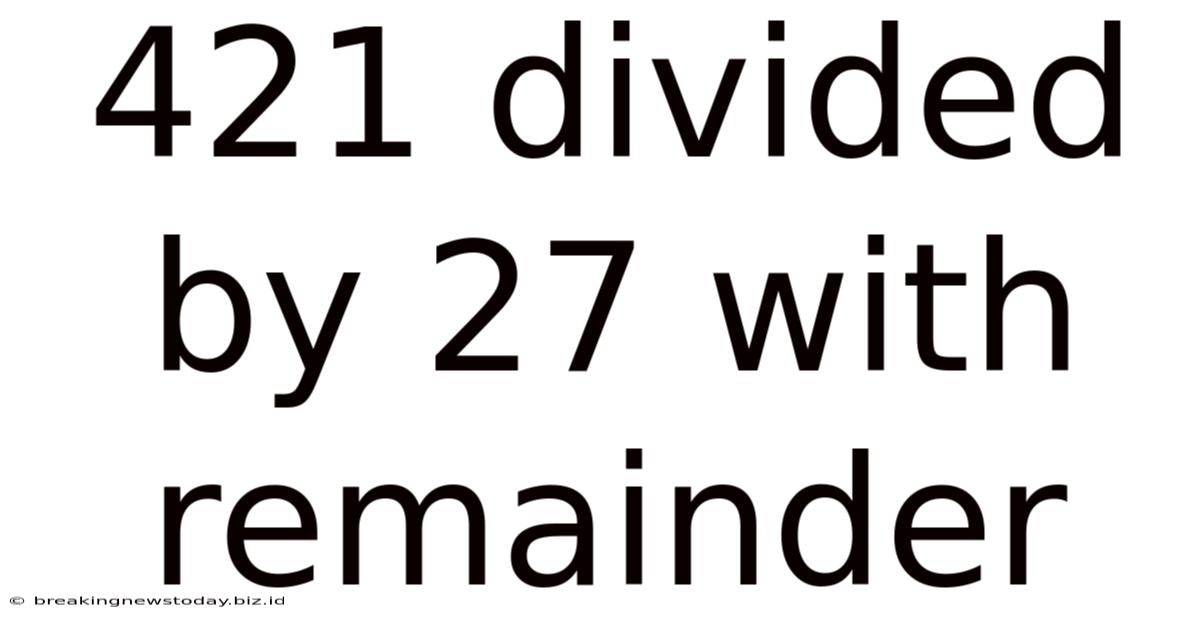
Table of Contents
421 Divided by 27: A Deep Dive into Division with Remainders
Understanding division, particularly division with remainders, is fundamental to mathematics. This seemingly simple operation forms the bedrock of more complex mathematical concepts and has practical applications in numerous fields. This article will explore the division of 421 by 27, dissecting the process, explaining the concept of remainders, and showcasing its relevance in various contexts. We'll delve into different methods of solving this problem, explore related mathematical concepts, and even touch upon the historical significance of division.
Understanding Division and Remainders
Division is the process of splitting a quantity into equal parts. When we divide a number (the dividend) by another number (the divisor), we aim to find how many times the divisor goes into the dividend evenly. Sometimes, the divisor doesn't go into the dividend perfectly. In such cases, we have a remainder – the amount left over after the division.
The standard way to represent division is:
Dividend ÷ Divisor = Quotient + Remainder/Divisor
Or, more formally:
Dividend = (Quotient × Divisor) + Remainder
In our case, the dividend is 421, and the divisor is 27. We'll explore how to find the quotient and the remainder.
Method 1: Long Division
Long division is a traditional method for performing division. It systematically breaks down the division process into smaller, manageable steps. Let's apply this to 421 ÷ 27:
-
Set up the problem: Write the dividend (421) inside the long division symbol and the divisor (27) outside.
-
Divide the first digit(s): 27 doesn't go into 4, so we consider the first two digits: 42. How many times does 27 go into 42? It goes in once (1). Write the 1 above the 2 in 42.
-
Multiply and subtract: Multiply the quotient (1) by the divisor (27): 1 × 27 = 27. Subtract this from 42: 42 - 27 = 15.
-
Bring down the next digit: Bring down the next digit from the dividend (1), making it 151.
-
Repeat the process: How many times does 27 go into 151? It goes in 5 times (5). Write the 5 above the 1 in 151.
-
Multiply and subtract: Multiply the quotient (5) by the divisor (27): 5 × 27 = 135. Subtract this from 151: 151 - 135 = 16.
-
Remainder: Since there are no more digits to bring down, 16 is the remainder.
Therefore, 421 ÷ 27 = 15 with a remainder of 16.
Method 2: Repeated Subtraction
This method involves repeatedly subtracting the divisor from the dividend until the result is less than the divisor. The number of times we subtract is the quotient, and the final result is the remainder.
-
Start with the dividend: 421
-
Repeatedly subtract the divisor (27):
- 421 - 27 = 394
- 394 - 27 = 367
- 367 - 27 = 340
- 340 - 27 = 313
- 313 - 27 = 286
- 286 - 27 = 259
- 259 - 27 = 232
- 232 - 27 = 205
- 205 - 27 = 178
- 178 - 27 = 151
- 151 - 27 = 124
- 124 - 27 = 97
- 97 - 27 = 70
- 70 - 27 = 43
- 43 - 27 = 16
-
Count the subtractions: We subtracted 27 fifteen times. This is our quotient.
-
The remainder is the final result: The final result after the repeated subtractions is 16. This is our remainder.
Therefore, 421 ÷ 27 = 15 with a remainder of 16.
Method 3: Using a Calculator
Most calculators can handle division with remainders. However, the way it displays the remainder might vary. Some calculators directly show the remainder, while others provide only the decimal representation. You'll need to convert the decimal portion back to a remainder if necessary. For this example, a calculator would show 15.592592... which means a remainder of 16 if you apply the formula shown above.
Practical Applications of Division with Remainders
Division with remainders isn't just an abstract mathematical concept; it has many practical applications in everyday life and various professional fields:
-
Sharing Equally: Dividing a certain number of items equally among a group of people, for instance, sharing 421 candies among 27 children, results in each child getting 15 candies with 16 candies leftover.
-
Grouping Items: Arranging objects into groups of a specific size is another example. Imagine arranging 421 chairs into rows of 27. You'd have 15 full rows and 16 chairs left over.
-
Scheduling: Calculating shift patterns or work schedules often requires dealing with remainders. If you need to assign tasks to 27 employees and you have 421 tasks, this division will guide the distribution.
-
Computer Science: In computer programming, division with remainders plays a crucial role in various algorithms and data structures. For instance, calculating array indices or handling data structures often involves modular arithmetic which relies heavily on the remainder operation (the modulo operator, denoted as %).
-
Engineering: In fields like engineering, division with remainders is used in calculating tolerances, machining, and many other industrial procedures.
-
Cryptography: Modular arithmetic (which relies heavily on remainders) is fundamental to modern cryptography, securing communications and online transactions.
Mathematical Concepts Related to Remainders
Several important mathematical concepts are closely linked to division with remainders:
-
Modular Arithmetic: This branch of number theory deals with remainders after division. It's used extensively in cryptography, computer science, and other fields. The modulo operator (%) is the central tool in modular arithmetic. The expression "421 mod 27" (read as "421 modulo 27") gives the remainder when 421 is divided by 27, which is 16.
-
Congruence: Two numbers are congruent modulo n if they have the same remainder when divided by n. For example, 421 and 16 are congruent modulo 27.
-
Greatest Common Divisor (GCD): The GCD of two numbers is the largest number that divides both without leaving a remainder. Algorithms like the Euclidean algorithm use division and remainders to efficiently compute the GCD.
Historical Context of Division
Division, and the handling of remainders, have been important since ancient civilizations. Evidence shows that Egyptians and Babylonians employed methods of division and developed techniques to address remainders in their calculations. Ancient Greek mathematicians like Euclid significantly contributed to the understanding of number theory, including division and related concepts like GCD. The development of long division as a standardized method evolved gradually over centuries.
Conclusion
Dividing 421 by 27 results in a quotient of 15 and a remainder of 16. This seemingly simple arithmetic operation is fundamental to mathematics and has wide-ranging applications in various fields. From everyday tasks to complex algorithms, understanding division with remainders is crucial. By mastering this fundamental concept, you equip yourself with a powerful tool for solving problems and understanding the world around you. Remember the formula: Dividend = (Quotient × Divisor) + Remainder and practice using different methods to solidify your understanding. The exploration of related concepts like modular arithmetic and the historical perspective further enriches our appreciation of this seemingly simple yet deeply significant mathematical operation.
Latest Posts
Latest Posts
-
Compare And Contrast Geology And Etymology
Jun 06, 2025
-
Which Sentence Contains The Strongest Use Of Emotional Connotation
Jun 06, 2025
-
Which Of The Following Describes Laminar Or Normal Airflow
Jun 06, 2025
-
Identify Three Safety Precautions For Loading And Unloading Helicopters
Jun 06, 2025
-
Which Choices Are Equivalent To The Expression Below
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about 421 Divided By 27 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.