43.7 Is What Percent Of 9.2
Breaking News Today
Jun 02, 2025 · 5 min read
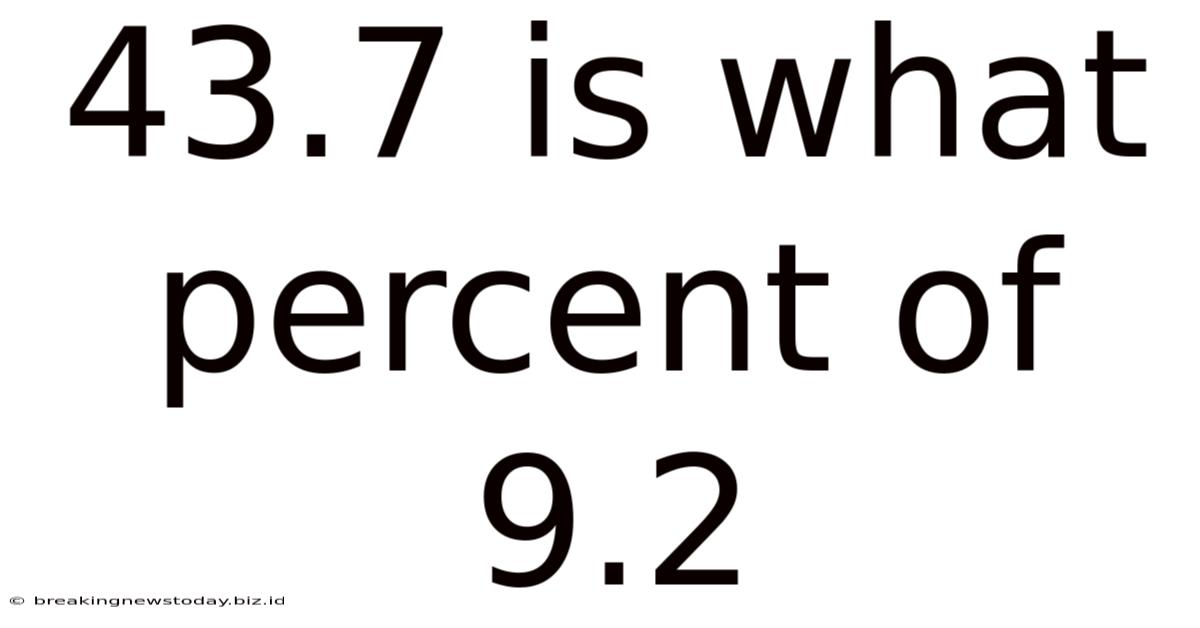
Table of Contents
43.7 is What Percent of 9.2? A Deep Dive into Percentage Calculations
This seemingly simple question, "43.7 is what percent of 9.2?", opens the door to a fascinating exploration of percentage calculations, their applications, and the underlying mathematical principles. While a simple calculator can provide the immediate answer, understanding the why behind the calculation is crucial for anyone wanting to master percentages and confidently apply them in various contexts. This article will not only provide the solution but also delve into the methodology, explore practical applications, and offer tips for accurately performing percentage calculations.
Understanding Percentages: The Fundamentals
Before tackling the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The term "percent" literally means "out of one hundred" (from the Latin per centum). For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
This fundamental understanding is key to solving percentage problems. We can represent any percentage as a decimal or a fraction, and vice-versa. This flexibility is crucial for different calculation methods.
Solving "43.7 is What Percent of 9.2?"
Now, let's address the central question: How do we determine what percentage 43.7 represents of 9.2? This isn't a straightforward case of a smaller number being a part of a larger number. Instead, we have a larger number (43.7) compared to a smaller number (9.2). This indicates that the percentage will be greater than 100%.
Here's how we solve it:
Step 1: Set up the equation:
We can express the problem as a proportion:
x / 100 = 43.7 / 9.2
Where 'x' represents the percentage we need to find.
Step 2: Solve for x:
To solve for 'x', we can cross-multiply:
9.2x = 43.7 * 100
9.2x = 4370
Now, divide both sides by 9.2:
x = 4370 / 9.2
x ≈ 475
Therefore, 43.7 is approximately 475% of 9.2.
Step 3: Verify the Result:
To verify this, we can calculate 475% of 9.2:
(475/100) * 9.2 = 4.75 * 9.2 = 43.7
This confirms our calculation.
Alternative Methods for Percentage Calculation
While the above method is straightforward, other approaches can be equally effective, depending on your comfort level with mathematical operations.
Method 2: Using Decimal Conversion:
-
Convert the percentage to a decimal: Divide the percentage by 100. For example, 25% becomes 0.25.
-
Multiply the decimal by the base number: Multiply the decimal by the number you want to find the percentage of.
Method 3: Using the Proportion Method:
The proportion method, demonstrated above, is highly versatile and works effectively for various percentage problems.
Practical Applications of Percentage Calculations
Understanding percentage calculations isn't just an academic exercise; it has widespread practical applications in various aspects of life:
1. Finance:
- Interest rates: Calculating interest earned on savings accounts or interest payable on loans.
- Investment returns: Determining the percentage increase or decrease in investment values.
- Discounts and sales tax: Computing discounts on products and adding sales tax to purchases.
- Financial analysis: Evaluating financial statements and assessing the profitability of businesses.
2. Science:
- Data analysis: Representing data using percentages to illustrate proportions and trends.
- Chemical concentrations: Expressing the concentration of substances in solutions as percentages.
- Statistical analysis: Calculating probabilities and representing data using percentages.
3. Everyday Life:
- Tipping in restaurants: Calculating appropriate tips based on the bill amount.
- Sales and discounts: Understanding discounts offered during sales events.
- Cooking and baking: Adjusting ingredient quantities based on percentage increases or decreases in recipes.
4. Business:
- Profit margins: Determining the percentage of profit relative to the cost of goods sold.
- Market share: Calculating the percentage of the market controlled by a particular company.
- Growth rates: Tracking the percentage growth of sales, revenue, or other key business metrics.
Common Mistakes to Avoid in Percentage Calculations
Even experienced individuals can make mistakes when dealing with percentages. Here are some common pitfalls to watch out for:
- Confusing percentages with decimal equivalents: Remember to convert percentages to decimals (divide by 100) before performing calculations.
- Incorrectly identifying the base number: Ensure you are calculating the percentage based on the correct base value.
- Rounding errors: Rounding intermediate results can lead to inaccuracies in the final answer. Aim to avoid rounding until the final step.
- Using the wrong formula: Different problems might require different formulas. Ensure you're using the correct approach for your specific situation.
Advanced Percentage Calculations
Beyond the basic calculations, there are more complex percentage problems that require a deeper understanding of the underlying principles:
- Percentage change: Calculating the percentage increase or decrease between two values. This involves finding the difference between the two values, dividing by the original value, and multiplying by 100.
- Compound interest: This involves calculating interest on both the principal amount and accumulated interest. This requires understanding exponential growth.
- Percentage points: This is a subtle but important distinction. A change of "x percentage points" means a direct addition or subtraction of x to the percentage, while an "x percent" change is calculated as described above.
Conclusion
The question, "43.7 is what percent of 9.2?" might seem simple at first glance, but it serves as an excellent springboard for exploring the world of percentage calculations. Mastering percentages requires not only understanding the basic formula but also comprehending the underlying concepts and avoiding common mistakes. This knowledge equips you with a powerful tool applicable across diverse fields, from finance and science to everyday life and business decisions. Remember to practice regularly, and with time, you will become proficient in tackling various percentage problems with confidence and accuracy. The key is understanding the why behind the calculations, not just the how.
Latest Posts
Latest Posts
-
What Was Clover Startled To Discover
Jun 04, 2025
-
Select 3 Options Writers Should Avoid Splitting An Infinitive When
Jun 04, 2025
-
Which Circuits Correctly Show Ohms Law
Jun 04, 2025
-
307 451 Rounded To The Nearest Thousand
Jun 04, 2025
-
In Calling Shantytowns Hoovervilles People Conveyed Their
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about 43.7 Is What Percent Of 9.2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.