5.6 Times The Sum Of 4 And A Number P
Breaking News Today
Jun 07, 2025 · 5 min read
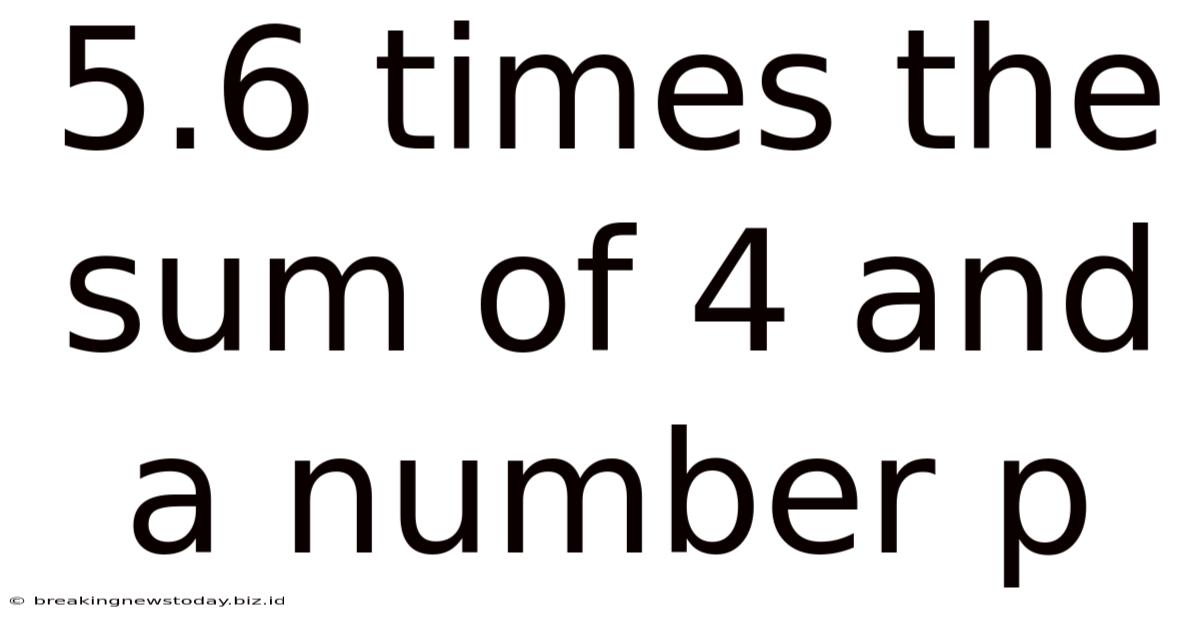
Table of Contents
Decoding "5.6 Times the Sum of 4 and a Number p": A Deep Dive into Mathematical Expressions and Problem-Solving
This article delves into the mathematical expression "5.6 times the sum of 4 and a number p," exploring its meaning, various interpretations, practical applications, and how to solve problems related to it. We'll move beyond the simple arithmetic to understand the underlying concepts and their broader implications in algebra and beyond. This comprehensive guide aims to equip you with the knowledge and skills to confidently tackle similar problems.
Understanding the Expression
The phrase "5.6 times the sum of 4 and a number p" translates directly into a mathematical expression: 5.6 * (4 + p). Let's break down each component:
- p: This represents an unknown number, a variable. It can take on any numerical value.
- 4 + p: This is the "sum of 4 and a number p." It signifies the addition of 4 and the value of p. This sum is then treated as a single entity.
- 5.6 * (4 + p): This shows the multiplication of 5.6 by the sum (4 + p). The parentheses are crucial; they indicate that the addition operation must be performed before the multiplication. This follows the order of operations (PEMDAS/BODMAS).
Illustrative Examples
Let's consider a few examples to solidify our understanding. We'll substitute different values for 'p' and calculate the resulting expression:
Example 1: p = 2
Substituting p = 2 into the expression 5.6 * (4 + p), we get:
5.6 * (4 + 2) = 5.6 * 6 = 33.6
Therefore, when p = 2, the expression evaluates to 33.6.
Example 2: p = -3
Substituting p = -3:
5.6 * (4 + (-3)) = 5.6 * 1 = 5.6
In this case, the expression equals 5.6.
Example 3: p = 0
Substituting p = 0:
5.6 * (4 + 0) = 5.6 * 4 = 22.4
When p = 0, the expression simplifies to 22.4.
These examples demonstrate how the value of the expression changes depending on the value assigned to the variable 'p'. This variability is fundamental to algebraic thinking.
Solving Equations Involving the Expression
Often, we encounter problems where the value of the expression is given, and we need to solve for the unknown 'p'. This involves setting up and solving an equation.
Example 4: Finding 'p' when the expression equals 78.4
Let's say the expression 5.6 * (4 + p) is equal to 78.4. We need to find the value of 'p'. We set up the equation:
5.6 * (4 + p) = 78.4
To solve this, we follow these steps:
- Divide both sides by 5.6: (4 + p) = 78.4 / 5.6 = 14
- Subtract 4 from both sides: p = 14 - 4 = 10
Therefore, when the expression equals 78.4, the value of p is 10.
Example 5: A More Complex Scenario
Let's consider a more intricate scenario. Suppose we have the equation:
2 * [5.6 * (4 + p)] - 10 = 52
Here, we have nested operations. To solve for 'p':
- Add 10 to both sides: 2 * [5.6 * (4 + p)] = 62
- Divide both sides by 2: 5.6 * (4 + p) = 31
- Divide both sides by 5.6: (4 + p) = 31 / 5.6 ≈ 5.5357
- Subtract 4 from both sides: p ≈ 5.5357 - 4 ≈ 1.5357
In this more complex example, we used approximate values due to the decimal nature of the numbers involved.
Real-World Applications
While this might seem like an abstract mathematical exercise, expressions like "5.6 times the sum of 4 and a number p" have practical applications in various fields:
- Finance: Calculating compound interest, determining total investment returns, or modeling profit margins can involve similar algebraic manipulations.
- Physics: Many physics formulas involve variables and constants, with calculations mirroring the structure of our expression. For example, calculating the total force acting on an object might involve summing multiple forces and then multiplying by a constant factor.
- Engineering: Designing structures, analyzing circuits, and managing resource allocation often involve similar calculations.
- Business: Calculating sales revenue based on a base price and variable factors.
Expanding the Concept: Generalizing the Expression
We can generalize the expression to explore its broader mathematical implications. Instead of specific numbers like 5.6 and 4, let's use variables:
a * (b + p)
Here, 'a' and 'b' are constants, and 'p' remains the variable. This generalized expression allows us to analyze a wider range of scenarios and develop more generalized problem-solving strategies. Solving for 'p' in this generalized form would involve similar steps as shown in the previous examples, but with variables instead of specific numbers.
Connecting to Other Mathematical Concepts
This seemingly simple expression connects to several important mathematical concepts:
- Algebra: The expression demonstrates the fundamental concepts of variables, constants, and operations. Solving for 'p' involves algebraic manipulation.
- Order of Operations: The parentheses emphasize the importance of following the order of operations (PEMDAS/BODMAS) to arrive at the correct answer.
- Functions: We can view this expression as a function, where the input is 'p' and the output is the result of the calculation. This allows us to explore concepts of domain, range, and function mapping.
Advanced Applications: Calculus and Beyond
At a more advanced level, this type of expression can be used in calculus. For instance, if we consider 'a' and 'b' as functions of another variable, then we can use calculus techniques (like differentiation or integration) to analyze the expression's behavior over different ranges.
Conclusion
The seemingly straightforward expression "5.6 times the sum of 4 and a number p" offers a rich platform to explore fundamental mathematical concepts. Through various examples and applications, we've seen how to interpret, manipulate, and solve problems involving this expression. Understanding the underlying principles not only strengthens your mathematical skills but also equips you to tackle more complex problems across different disciplines. This exploration emphasizes the power of mathematical notation and its connection to real-world applications. The ability to translate word problems into mathematical expressions and subsequently solve those expressions is a critical skill for success in many academic and professional endeavors. Remember to always pay attention to the order of operations and the meaning behind each component of the expression to ensure accuracy in your calculations.
Latest Posts
Latest Posts
-
Proficiency In Multiple Languages Demonstrates Your Ability To Succeed
Jun 07, 2025
-
All Queries Have A Task Language And Task Location
Jun 07, 2025
-
The Following Are Good Customer Service Strategies Except
Jun 07, 2025
-
A Woman Stands A Distance D From A Loud Motor
Jun 07, 2025
-
1 3h 4 2 3h 3 2 3h 6
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 5.6 Times The Sum Of 4 And A Number P . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.