5 Less Than 3.1 Times A Number N
Breaking News Today
Jun 02, 2025 · 5 min read
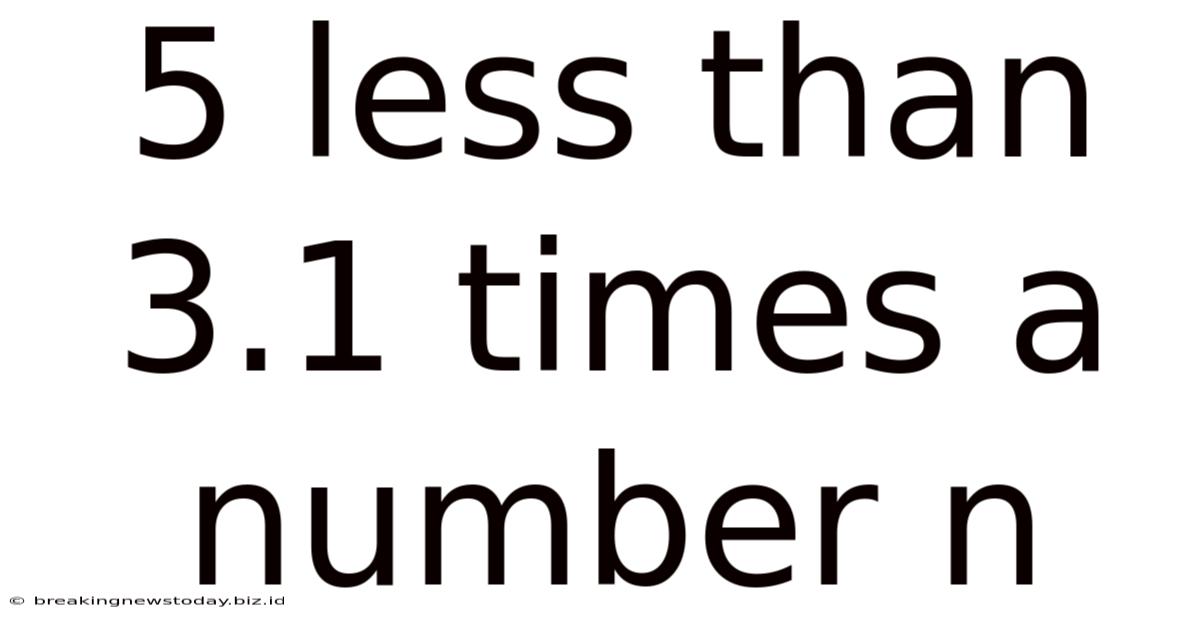
Table of Contents
5 Less Than 3.1 Times a Number: Exploring Mathematical Expressions and Problem Solving
This article delves into the mathematical expression "5 less than 3.1 times a number n," exploring its translation into algebraic form, solving for 'n' given different scenarios, real-world applications, and extending the concept to more complex equations. We'll examine various problem-solving techniques and illustrate their application with detailed examples. This comprehensive guide is designed to enhance your understanding of algebraic expressions and problem-solving strategies.
Understanding the Expression: "5 Less Than 3.1 Times a Number n"
The phrase "5 less than 3.1 times a number n" can be deceptively simple, yet understanding its structure is crucial for accurate mathematical representation. Let's break it down step-by-step:
- "a number n": This represents an unknown quantity, which we denote by the variable 'n'.
- "3.1 times a number n": This translates directly to the algebraic expression 3.1n (or 3.1 * n). Multiplication is implied by the word "times".
- "5 less than": This signifies subtraction. We subtract 5 from the result of "3.1 times a number n."
Therefore, the complete algebraic representation of the phrase "5 less than 3.1 times a number n" is 3.1n - 5.
Solving for 'n' in Different Scenarios
The expression 3.1n - 5 can be used in various mathematical problems. The solution for 'n' depends on the value of the entire expression. Let's explore a few scenarios:
Scenario 1: The Expression Equals a Specific Value
Let's say the expression "5 less than 3.1 times a number n" is equal to 10.6. This translates to the equation:
3.1n - 5 = 10.6
To solve for 'n', we follow these steps:
- Add 5 to both sides: 3.1n = 15.6
- Divide both sides by 3.1: n = 15.6 / 3.1 = 5
Therefore, in this scenario, n = 5.
Scenario 2: The Expression is Greater Than or Less Than a Specific Value
Suppose the expression is greater than 20. This translates to the inequality:
3.1n - 5 > 20
Solving this inequality:
- Add 5 to both sides: 3.1n > 25
- Divide both sides by 3.1: n > 25 / 3.1 ≈ 8.06
This means that 'n' must be greater than approximately 8.06 to satisfy the inequality.
Similarly, if the expression is less than 10:
3.1n - 5 < 10
Solving this inequality:
- Add 5 to both sides: 3.1n < 15
- Divide both sides by 3.1: n < 15 / 3.1 ≈ 4.84
In this case, 'n' must be less than approximately 4.84.
Scenario 3: Solving for 'n' when the Expression Involves Other Variables
Let's introduce another variable, 'x', into the equation:
3.1n - 5 = x
In this case, solving for 'n' requires expressing 'n' in terms of 'x':
- Add 5 to both sides: 3.1n = x + 5
- Divide both sides by 3.1: n = (x + 5) / 3.1
This shows how the solution for 'n' changes based on the context of the problem.
Real-World Applications
While this might seem like a purely mathematical exercise, the concept of "5 less than 3.1 times a number" has practical applications in various fields:
-
Business and Finance: Imagine calculating profit where the profit margin is 3.1 times the number of units sold, but there are fixed costs of 5 units. The expression 3.1n - 5 could represent the total profit (n being the number of units sold).
-
Science and Engineering: In physics or engineering, this type of expression could model a relationship between variables, where the value of one variable depends linearly on another, with an offset of 5 units.
-
Everyday Life: Think about scenarios involving discounts. If an item costs 3.1 times its original price, and you get a discount of 5 units, this expression could represent the final price.
Extending the Concept: More Complex Equations
The foundational understanding of "5 less than 3.1 times a number n" can be applied to more intricate mathematical problems. Let's consider a few examples:
Example 1: Quadratic Equations
Imagine we have an equation involving the square of 'n':
(3.1n - 5)² = 100
To solve this, we would first take the square root of both sides:
3.1n - 5 = ±10
This gives us two separate equations to solve:
3.1n - 5 = 10 and 3.1n - 5 = -10
Solving each equation using the steps outlined above yields two solutions for 'n'.
Example 2: Systems of Equations
Consider a system of two equations involving 'n' and another variable 'm':
3.1n - 5 = m n + m = 20
We can solve this system using substitution or elimination methods to find the values of both 'n' and 'm'.
Example 3: Exponential Equations
Imagine 'n' is an exponent:
3.1ⁿ - 5 = 10
Solving exponential equations typically involves logarithms. In this case, we would first add 5 to both sides, then take the logarithm of both sides to solve for 'n'.
Conclusion: Mastering Algebraic Expressions and Problem Solving
Understanding the simple, yet fundamental, expression "5 less than 3.1 times a number n" provides a solid foundation for tackling more complex mathematical problems. The ability to translate verbal descriptions into algebraic expressions and solve for unknown variables is a crucial skill in numerous academic and professional fields. By mastering these concepts and practicing various problem-solving techniques, you will significantly enhance your mathematical abilities and problem-solving skills. Remember to break down complex problems into smaller, more manageable steps and always double-check your work. Continuous practice and a willingness to explore different approaches will lead to a deeper understanding and greater confidence in your mathematical capabilities. The key takeaway is the ability to translate real-world situations into mathematical models, and then use algebraic techniques to solve for unknown values. This skill is not just about numbers; it's about critical thinking and analytical problem-solving.
Latest Posts
Latest Posts
-
Discriminatory Acts Are Always Accompanied By Prejudiced Attitudes
Jun 04, 2025
-
For The Distribution Drawn Here Identify The Mean
Jun 04, 2025
-
Which Two Statements About Composite Materials Are True
Jun 04, 2025
-
Objects In A Composition Occupy
Jun 04, 2025
-
Which Approach Is Intended To Prevent Exploits That Target Syslog
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about 5 Less Than 3.1 Times A Number N . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.