5 Ones 3 Tenths - 0.53
Breaking News Today
Jun 05, 2025 · 5 min read
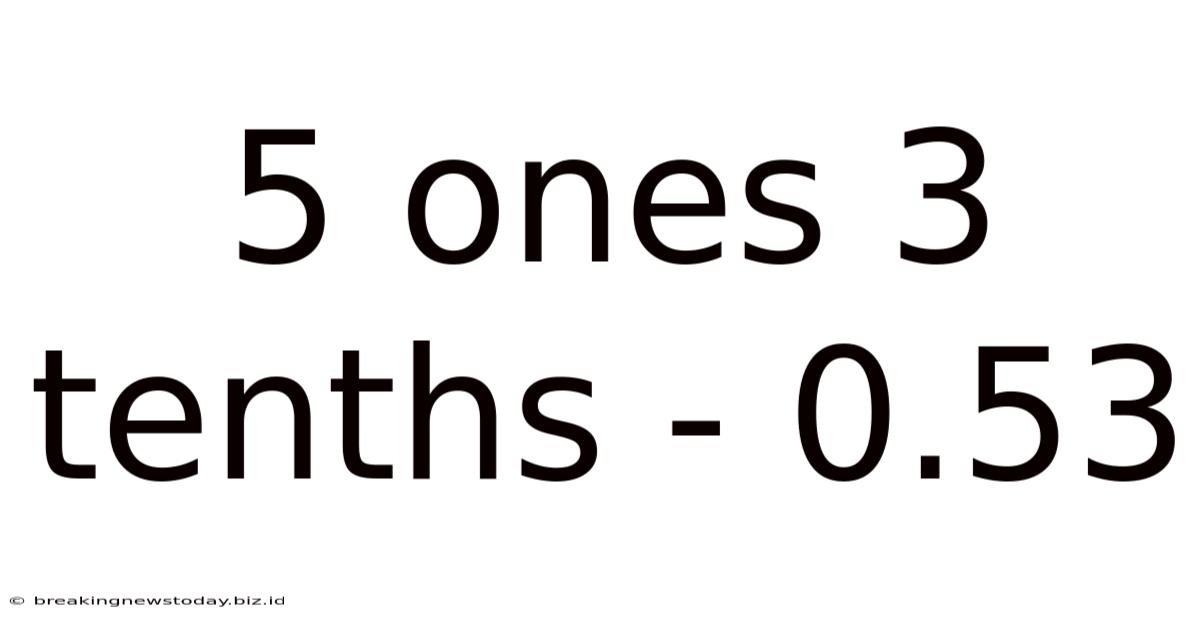
Table of Contents
Decoding 5 Ones 3 Tenths - 0.53: A Deep Dive into Decimal Subtraction
This article will comprehensively explore the subtraction problem "5 ones 3 tenths - 0.53," breaking down the concept into easily digestible parts. We'll delve into the fundamental principles of decimal numbers, subtraction methods, and practical applications, ensuring a complete understanding for all readers, regardless of their mathematical background. This in-depth analysis will also cover related concepts and explore diverse approaches to solve similar problems, making it a valuable resource for students, educators, and anyone seeking to enhance their numerical literacy.
Understanding Decimal Numbers: A Foundation
Before tackling the subtraction, let's solidify our understanding of decimal numbers. A decimal number is a number that uses a decimal point to separate the whole number part from the fractional part. The digits to the left of the decimal point represent whole numbers (ones, tens, hundreds, and so on), while the digits to the right represent fractions (tenths, hundredths, thousandths, and so on).
Key Terminology:
- Ones: The place value immediately to the left of the decimal point.
- Tenths: The place value immediately to the right of the decimal point.
- Hundredths: The place value one place to the right of the tenths.
- Decimal Point: The symbol (.) separating the whole number part from the fractional part.
In our problem, "5 ones 3 tenths," the '5' represents five whole units, and the '3' represents three-tenths (3/10 or 0.3). This can be written as 5.3. Understanding this basic structure is crucial for successful decimal subtraction.
Different Representations of the Same Number
It's important to recognize that the number "5 ones 3 tenths" can be expressed in multiple ways:
- Word form: Five ones and three tenths
- Expanded form: 5 + 0.3
- Decimal form: 5.3
- Fraction form: 5 3/10
Understanding these different representations enhances flexibility and problem-solving skills. The ability to switch between these forms is a valuable tool for tackling more complex mathematical problems.
Tackling the Subtraction: 5.3 - 0.53
Now, let's directly address the subtraction problem: 5.3 - 0.53. We can approach this using several methods, each offering a unique perspective and strengthening our understanding of decimal operations.
Method 1: Vertical Subtraction with Place Value Alignment
This classic method emphasizes the importance of aligning decimal points and place values.
5.30
- 0.53
-------
4.77
Explanation:
- Align Decimal Points: Ensure the decimal points are vertically aligned.
- Add Zeroes: Add a zero to the hundredths place of 5.3 to make the subtraction easier. This doesn't change the value of 5.3 (5.30 = 5.3).
- Subtract from Right to Left: Subtract the hundredths, then the tenths, and finally the ones. Borrowing (regrouping) may be necessary, as seen in this example (we borrow from the ones place to subtract in the tenths place).
Method 2: Converting to Fractions
Converting the decimals to fractions can provide a different perspective and strengthen fractional arithmetic skills.
5.3 = 53/10 0.53 = 53/100
To subtract, we need a common denominator:
53/10 = 530/100
Now we can subtract:
530/100 - 53/100 = 477/100 = 4.77
Method 3: Using a Number Line
A visual representation using a number line can be helpful, particularly for younger learners. Start at 5.3 and move 0.53 units to the left. This visual method reinforces the concept of subtraction as taking away a value. Although less practical for complex problems, it's excellent for building foundational understanding.
Method 4: Breaking Down the Subtraction
This method involves separating the subtraction into smaller, more manageable steps.
5.3 - 0.53 = (5 - 0.5) + (0.3 - 0.03) = 4.5 + 0.27 = 4.77
Practical Applications and Real-World Scenarios
Understanding decimal subtraction is essential for countless real-world applications. Consider these scenarios:
- Financial Calculations: Calculating change after a purchase, balancing a checkbook, tracking expenses.
- Measurement: Measuring lengths, weights, and volumes using metric units.
- Scientific Calculations: Performing calculations in chemistry, physics, and other scientific fields.
- Data Analysis: Working with data sets that include decimal values.
- Cooking and Baking: Following recipes that involve precise measurements.
Expanding Knowledge: Further Exploration
Once you've mastered the basics of 5.3 - 0.53, consider exploring these related concepts:
- Adding Decimals: Practice addition problems involving decimals to solidify your understanding of decimal operations.
- Multiplying Decimals: Learn how to multiply decimal numbers, which requires a slightly different approach than addition or subtraction.
- Dividing Decimals: Mastering division with decimals requires understanding how to adjust the decimal point in the dividend and divisor.
- Rounding Decimals: Learn how to round decimals to a specific number of decimal places. This skill is crucial for simplifying calculations and representing values concisely.
- Working with Negative Decimals: Expand your skills to include subtraction and other operations with negative decimal numbers.
Troubleshooting and Common Mistakes
Many students struggle with decimal subtraction due to several common mistakes:
- Misaligning Decimal Points: This leads to incorrect place value alignment and inaccurate results. Always ensure the decimal points are vertically aligned.
- Forgetting to Add Zeroes: Adding zeroes as placeholders is essential, especially when subtracting decimals with different numbers of decimal places.
- Incorrect Borrowing: Borrowing (regrouping) requires careful attention. A slight error in borrowing can lead to a significantly incorrect answer.
- Lack of Understanding Place Value: A strong understanding of place value is foundational to successful decimal operations.
By carefully avoiding these common errors and practicing regularly, you'll develop confidence and accuracy in your decimal subtraction skills.
Conclusion: Mastering Decimal Subtraction
This in-depth analysis of the problem "5 ones 3 tenths - 0.53" has explored various approaches, practical applications, and potential pitfalls. By understanding the underlying principles of decimal numbers and employing a methodical approach, you can confidently solve decimal subtraction problems of any complexity. Remember that consistent practice is key to mastering any mathematical concept. Embrace the learning process, explore different methods, and don't hesitate to seek help when needed. With dedication and perseverance, you'll become proficient in decimal subtraction and build a strong foundation for more advanced mathematical concepts. The journey to mathematical fluency is a rewarding one – embrace the challenge and enjoy the process of discovery!
Latest Posts
Latest Posts
-
Which Best Describes The Theme Of Sympathy
Jun 06, 2025
-
Create A Timeline That Illustrates The Major Events In Decomposition
Jun 06, 2025
-
What Is The Ph Of A 0 00125 M Hcl Solution
Jun 06, 2025
-
The Tables Represent Two Linear Functions In A System
Jun 06, 2025
-
You Hear Es Mi Diccionario De Espa Ol You Choose My
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about 5 Ones 3 Tenths - 0.53 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.