50 Is 8 Of What Number
Breaking News Today
Jun 01, 2025 · 5 min read
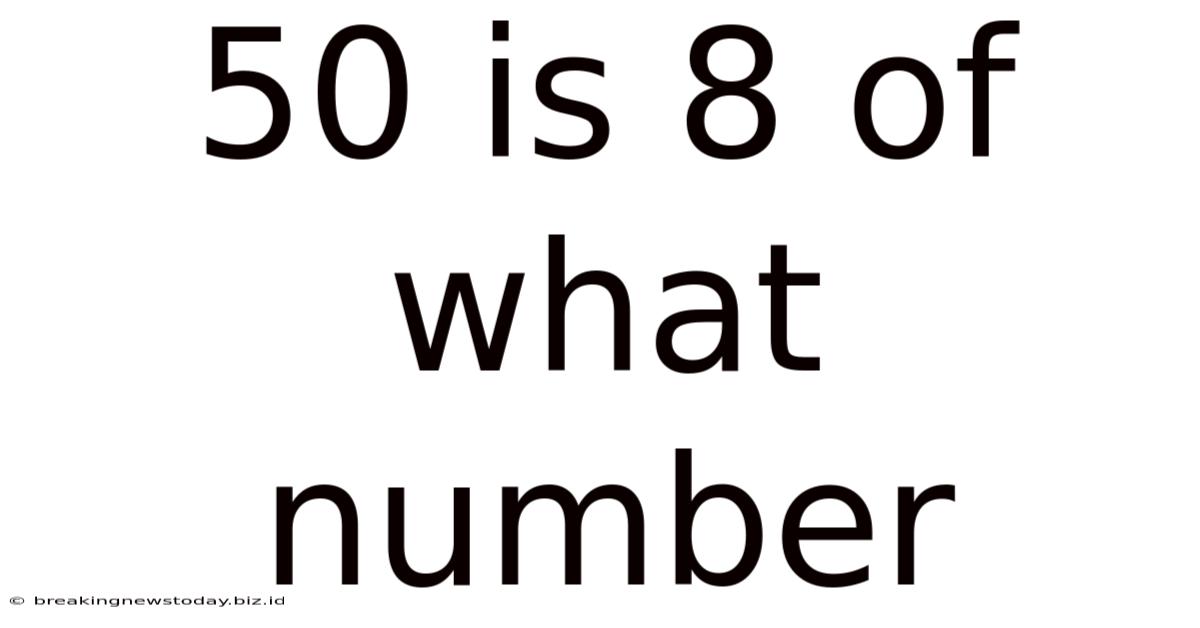
Table of Contents
50 is 8% of What Number? A Deep Dive into Percentage Calculations
Finding a number when you know a percentage of it is a common mathematical problem encountered in various real-life situations. Whether you're calculating discounts, figuring out tax amounts, or analyzing financial data, understanding how to solve these types of problems is crucial. This article will delve into the process of determining what number 50 represents when it's 8% of a larger, unknown number. We'll explore multiple approaches, discuss the underlying mathematical principles, and provide practical examples to solidify your understanding.
Understanding Percentages
Before we tackle the core problem, let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. For example, 8% can be written as 8/100 or 0.08 in decimal form. This means that 8% represents 8 parts out of every 100 parts of a whole.
Method 1: Using Proportions
Proportions offer a straightforward and intuitive way to solve percentage problems. We can set up a proportion to represent the relationship between the known percentage (8%), the known part (50), and the unknown whole (let's call it 'x').
The proportion can be expressed as:
8/100 = 50/x
This equation states that the ratio of 8 to 100 is equal to the ratio of 50 to x. To solve for x, we can cross-multiply:
8x = 50 * 100
8x = 5000
x = 5000 / 8
x = 625
Therefore, 50 is 8% of 625.
Method 2: Using the Decimal Equivalent
Another effective approach involves converting the percentage to its decimal equivalent and setting up an equation. As mentioned earlier, 8% is equivalent to 0.08. We can then express the problem as an equation:
0.08 * x = 50
To solve for x, we divide both sides of the equation by 0.08:
x = 50 / 0.08
x = 625
This method yields the same result as the proportion method, confirming that 50 is 8% of 625.
Method 3: Working Backwards from the Percentage
This approach involves thinking about the problem in reverse. If 50 represents 8%, what does 1% represent? We can find this by dividing 50 by 8:
50 / 8 = 6.25
This means that 1% of the unknown number is 6.25. To find the whole number (100%), we simply multiply this value by 100:
6.25 * 100 = 625
Again, this confirms that 50 is 8% of 625.
Practical Applications: Real-World Scenarios
Understanding percentage calculations is vital in many real-life situations. Let's explore a few examples:
Example 1: Sales and Discounts
Imagine a store is offering an 8% discount on an item originally priced at $625. To calculate the discount amount, we would perform the same calculation as above:
8% of $625 = 0.08 * $625 = $50
The discount is $50, resulting in a final price of $625 - $50 = $575.
Example 2: Tax Calculations
If a sales tax is 8% and the tax amount on a purchase is $50, we can determine the original price of the purchase using the methods described above:
The original price is $625.
Example 3: Financial Analysis
Percentage calculations are crucial in financial analysis. For example, if a company's profit margin is 8% and the profit is $50,000, then the company's revenue is:
$50,000 / 0.08 = $625,000
Example 4: Grade Calculations
Suppose a student earned 50 points on a test, and this score represents 8% of the total possible points. To find the total possible points, we'd again utilize the same approach:
50 / 0.08 = 625 points.
Beyond the Basics: Dealing with More Complex Percentages
While the problem "50 is 8% of what number?" presents a relatively straightforward calculation, the underlying principles can be applied to more complex percentage problems. These might involve:
- Multiple percentages: For instance, calculating a final price after applying multiple discounts or taxes.
- Compound interest: Understanding how interest accumulates over time.
- Percentage increase/decrease: Determining the percentage change between two values.
Mastering these fundamental percentage calculations lays a solid foundation for tackling more advanced problems. It's important to practice these calculations regularly to develop fluency and confidence in applying them to different real-world situations.
Troubleshooting Common Mistakes
Even seemingly simple percentage problems can lead to errors if certain steps aren't followed meticulously. Here are some common mistakes to watch out for:
- Incorrect Decimal Conversion: Ensure you accurately convert the percentage to its decimal equivalent before performing calculations. 8% should always be converted to 0.08, not 0.8.
- Mixing Up the Formula: Remember the correct formula for percentage calculations: Part/Whole = Percentage/100.
- Calculation Errors: Double-check your arithmetic to avoid errors in multiplication or division. Using a calculator can help to prevent this type of mistake.
- Misinterpreting the Problem: Carefully read and understand the wording of the problem to ensure you're setting up the correct equation.
By being mindful of these common errors, you can significantly improve the accuracy of your percentage calculations.
Conclusion: Mastering Percentage Calculations
The question, "50 is 8% of what number?" provides an excellent entry point into the world of percentage calculations. We've explored three different methods to solve this problem, emphasizing the importance of understanding the underlying mathematical principles. By understanding proportions, decimal equivalents, and working backwards from the percentage, you can approach these problems with confidence and accuracy. The applications of percentage calculations extend far beyond simple mathematical exercises, impacting areas such as finance, sales, and even academic grading. Mastering these skills is crucial for navigating the numerical aspects of everyday life and professional endeavors. Practice regularly and hone your skills to enhance your problem-solving capabilities and overall numerical literacy. Remember to always double-check your work and avoid common errors to ensure accuracy in your calculations.
Latest Posts
Latest Posts
-
A Vehicle Should Never Be Parked Closer
Jun 03, 2025
-
Selective Disclosure Is A Privacy Design Pattern Used For Implementing
Jun 03, 2025
-
Believing That People Tend To Make Sound Financial Decisions
Jun 03, 2025
-
How Often Does The Line Y 1 Intersect The Graph
Jun 03, 2025
-
A Series Of Exercises Interspersed With Rest Periods Best Describes
Jun 03, 2025
Related Post
Thank you for visiting our website which covers about 50 Is 8 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.