5x - 4 - 8x + 10
Breaking News Today
Jun 06, 2025 · 4 min read
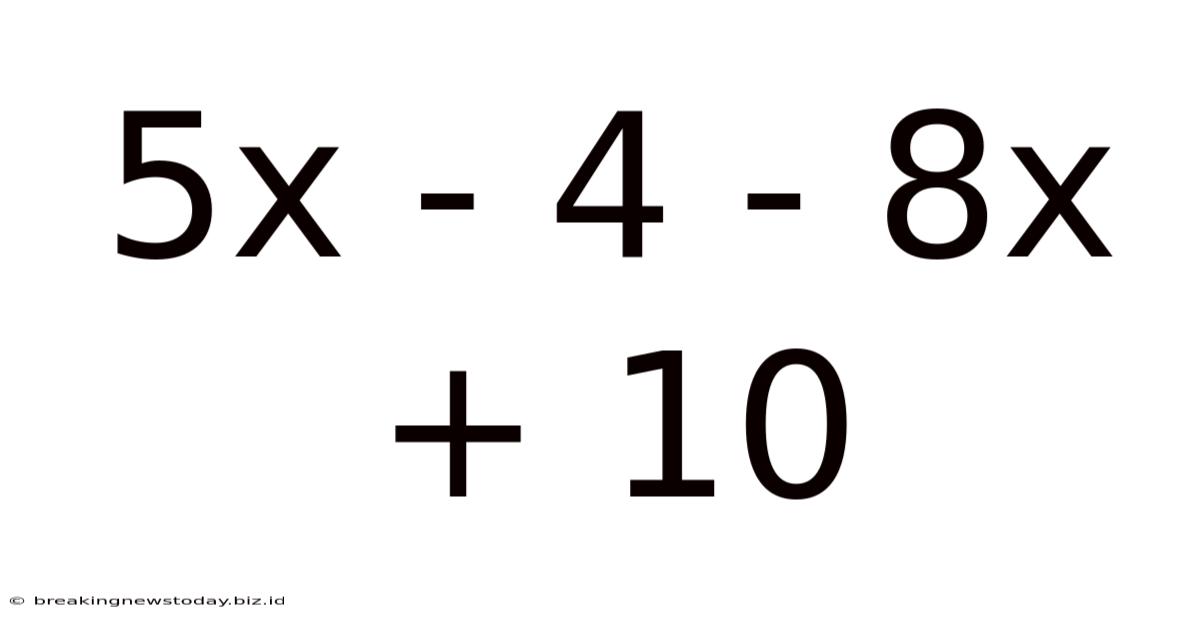
Table of Contents
Simplifying and Solving Algebraic Expressions: A Deep Dive into 5x - 4 - 8x + 10
This article provides a comprehensive exploration of the algebraic expression 5x - 4 - 8x + 10, covering simplification, solving for x, and extending the concepts to more complex scenarios. We'll delve into the fundamental principles of algebra, emphasizing practical applications and problem-solving techniques. Understanding this seemingly simple expression forms the bedrock for tackling more advanced algebraic concepts.
Understanding the Components
Before simplifying, let's break down the expression into its individual components:
- 5x: This term represents 5 multiplied by an unknown variable, 'x'. The '5' is called the coefficient, and 'x' is the variable.
- -4: This is a constant term, a numerical value without a variable.
- -8x: Similar to 5x, this is a term with a coefficient (-8) and the variable (x).
- +10: Another constant term.
Understanding these components is crucial for performing the simplification process correctly.
Simplifying the Expression
Simplifying an algebraic expression involves combining like terms. Like terms are terms that have the same variable raised to the same power. In our expression, 5x and -8x are like terms, and -4 and +10 are like terms.
Let's combine the like terms:
5x - 8x = -3x (We subtract the coefficients: 5 - 8 = -3)
-4 + 10 = 6 (We add the constants: -4 + 10 = 6)
Therefore, the simplified expression is:
-3x + 6
This simplified form is equivalent to the original expression, but it's more concise and easier to work with.
Solving for x
While simplification makes the expression easier to handle, solving for 'x' requires more steps. Solving for 'x' means finding the value of 'x' that makes the expression equal to zero (or any other specified value). To do this, we typically set the expression equal to zero and then use algebraic manipulation to isolate 'x'.
-3x + 6 = 0
Now, we isolate 'x' using the following steps:
-
Subtract 6 from both sides: -3x = -6
-
Divide both sides by -3: x = 2
Therefore, the solution to the equation -3x + 6 = 0 is x = 2. This means that if we substitute x = 2 back into the original expression (5x - 4 - 8x + 10), the result will be zero. Let's verify:
5(2) - 4 - 8(2) + 10 = 10 - 4 - 16 + 10 = 0
The solution is correct.
Extending the Concepts: More Complex Scenarios
The principles applied to 5x - 4 - 8x + 10 can be extended to more complex algebraic expressions. Let's consider some examples:
Example 1: Expressions with Parentheses
Consider the expression: 2(3x - 1) - 4x + 5
First, we need to distribute the '2' to the terms inside the parentheses:
2(3x - 1) = 6x - 2
Now, rewrite the expression:
6x - 2 - 4x + 5
Combine like terms:
6x - 4x = 2x
-2 + 5 = 3
The simplified expression is: 2x + 3
To solve for x, we set the expression equal to zero:
2x + 3 = 0
2x = -3
x = -3/2 or x = -1.5
Example 2: Expressions with Exponents
Consider the expression: 4x² + 2x - 8x² + 5x - 2
Combine like terms:
4x² - 8x² = -4x²
2x + 5x = 7x
The simplified expression is: -4x² + 7x - 2
Solving for x in a quadratic equation like this requires more advanced techniques, such as factoring, the quadratic formula, or completing the square. These methods are beyond the scope of this basic introduction.
Example 3: Expressions with Fractions
Consider the expression: (1/2)x + 3 - (3/4)x + 1
To combine the x terms, find a common denominator:
(1/2)x - (3/4)x = (2/4)x - (3/4)x = -(1/4)x
Combine the constant terms:
3 + 1 = 4
The simplified expression is: -(1/4)x + 4
Applications in Real-World Problems
Algebraic expressions like the ones we've explored aren't just abstract concepts; they have numerous practical applications. They are fundamental tools used in:
- Physics: Calculating motion, forces, and energy.
- Engineering: Designing structures, circuits, and systems.
- Economics: Modeling supply and demand, and analyzing financial data.
- Computer Science: Developing algorithms and data structures.
Understanding how to simplify and solve these expressions is therefore crucial for success in many fields.
Conclusion
The simple algebraic expression 5x - 4 - 8x + 10, while seemingly basic, serves as an excellent introduction to fundamental algebraic principles. Through simplification and solving for x, we’ve demonstrated the power of combining like terms and manipulating equations to find solutions. This foundation is crucial for tackling more complex problems in algebra and its diverse real-world applications. Mastering these concepts opens the door to a deeper understanding of mathematical modeling and problem-solving. Remember to practice regularly to build your confidence and proficiency in algebra. The more you practice, the easier these manipulations will become. By diligently working through examples and challenging yourself with progressively more difficult expressions, you'll solidify your understanding and build a solid foundation for future mathematical endeavors.
Latest Posts
Latest Posts
-
600 Is 10 Times As Much As
Jun 07, 2025
-
Choose The Statement That Best Describes Superinfection
Jun 07, 2025
-
A Tube Is Being Stretched While Maintaining Its Cylindrical Shape
Jun 07, 2025
-
Quiz 7 2 Parallelograms Rectangles Rhombi And Squares Answer Key
Jun 07, 2025
-
A Mattress Store Sold 1 330
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 5x - 4 - 8x + 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.