5x Y 5 3x 6y 24
Breaking News Today
Jun 08, 2025 · 6 min read
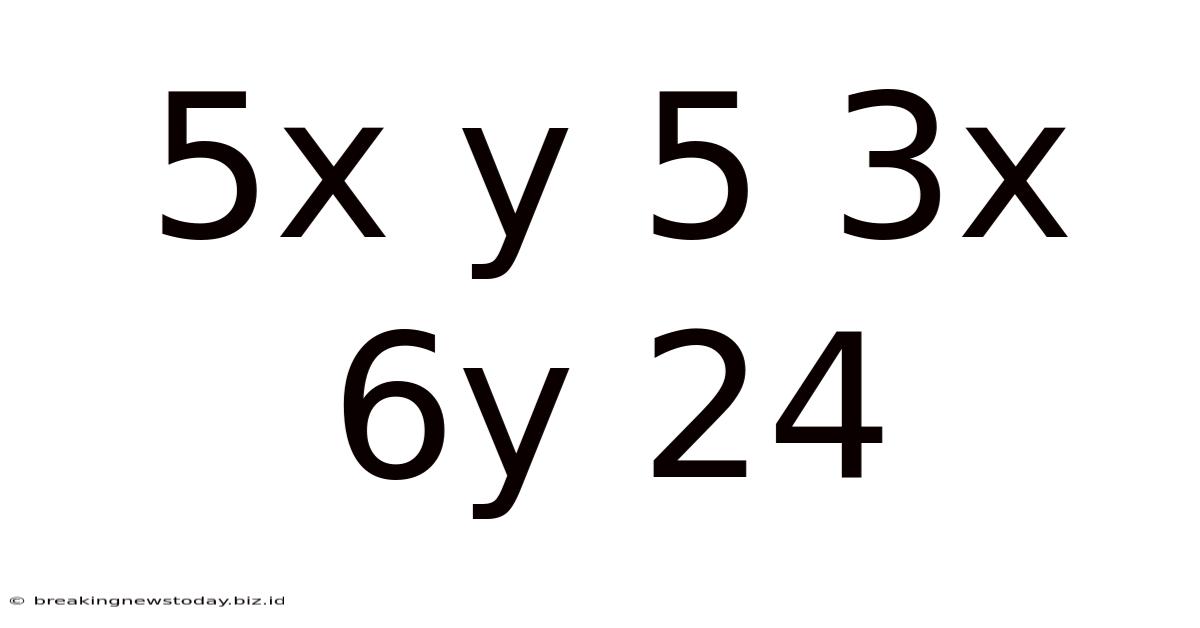
Table of Contents
Decoding the Math: A Deep Dive into 5x + 5 = 3x + 6y = 24
This seemingly simple equation, 5x + 5 = 3x + 6y = 24, presents a fascinating challenge in algebra. At first glance, it might seem straightforward, but unraveling its secrets requires a methodical approach and a solid understanding of algebraic manipulation. This article will explore this equation in detail, breaking down the solution process, discussing potential applications, and even exploring some related mathematical concepts. Let's dive in!
Understanding the Structure of the Equation
The core of the problem lies in the fact that we have a single equation with two variables, x and y. This means we don't have a unique solution; instead, we'll be looking for a relationship between x and y that satisfies the equation. The equation is actually a system of two equations disguised as one:
- Equation 1: 5x + 5 = 24
- Equation 2: 3x + 6y = 24
This separation is key to finding our solutions. Let's tackle each equation separately.
Solving Equation 1: 5x + 5 = 24
This is a simple linear equation. Our goal is to isolate 'x'.
- Subtract 5 from both sides: 5x = 19
- Divide both sides by 5: x = 19/5 or 3.8
Therefore, the solution for x in Equation 1 is x = 3.8.
Solving Equation 2: 3x + 6y = 24
This equation requires a slightly more involved process because it contains two variables. However, since we've already solved for x in Equation 1, we can substitute that value into this equation to solve for y.
- Substitute x = 3.8: 3(3.8) + 6y = 24
- Simplify: 11.4 + 6y = 24
- Subtract 11.4 from both sides: 6y = 12.6
- Divide both sides by 6: y = 12.6/6 = 2.1
Therefore, the solution for y in Equation 2, given x = 3.8, is y = 2.1.
The Solution Set and its Implications
We've found a solution pair: x = 3.8 and y = 2.1. However, it's crucial to understand that this isn't the only solution. Because we have two variables and essentially two equations (hidden within one), there's likely an infinite number of solutions if we don't treat it as a system of equations. If we consider each part separately, then we are solving for two different linear equations.
Let's analyze the implications:
- Equation 1 (5x + 5 = 24) provides a single solution for x. This is because it's a standard linear equation in one variable.
- Equation 2 (3x + 6y = 24) represents a line on a coordinate plane. For every value of x, there's a corresponding value of y that satisfies the equation. This is because it's a linear equation in two variables.
Because we solved Equation 1 independently, it's a specific point on the line represented by Equation 2. Different approaches could yield different sets of possible solutions. For instance, if we first solved for y in Equation 2 and then substituted into Equation 1, we might have gotten a different result.
The key takeaway is that the initial presentation of the equation is misleading. It suggests a single solution, but the reality is more nuanced. It highlights the importance of carefully analyzing the structure of an equation before attempting to solve it.
Exploring Related Mathematical Concepts
This seemingly simple equation touches upon several important mathematical concepts:
- Linear Equations: Both parts of the equation are linear equations, meaning they represent straight lines when graphed. Understanding the properties of linear equations is fundamental to solving this type of problem.
- Systems of Equations: While not explicitly stated as such, the problem effectively presents a system of two linear equations in two variables. Solving systems of equations is a crucial skill in algebra and has wide-ranging applications in various fields.
- Substitution Method: The approach we used to solve the problem employed the substitution method, a common technique for solving systems of equations. This involves solving one equation for one variable and then substituting that expression into the other equation.
- Graphical Representation: Visualizing the equations as lines on a coordinate plane can provide valuable insights into the nature of the solutions. The point of intersection (if it exists) represents a solution to the system of equations.
Applications in Real-World Scenarios
While this specific equation might not have an immediate, obvious real-world application, the underlying mathematical concepts are widely used in various fields:
- Engineering: Linear equations are fundamental to many engineering problems, such as calculating forces, designing structures, and modeling electrical circuits.
- Economics: Economic models often involve systems of linear equations to represent relationships between variables like supply and demand, income and expenditure.
- Physics: Linear equations are used extensively in physics to describe motion, forces, and energy relationships.
- Computer Science: Linear algebra, which deals with systems of linear equations, is crucial in computer graphics, machine learning, and data analysis.
Understanding how to solve these types of equations is therefore valuable, even if the specific equation itself doesn't have a direct practical application.
Advanced Considerations and Further Exploration
Let's delve deeper into the possibilities by considering what would happen if we treated the equation as a single entity and looked for possible integer solutions. We need to find integer values of x and y that satisfy both 5x + 5 = 24 and 3x + 6y = 24.
If we focus on 5x + 5 = 24:
- 5x = 19
- x = 19/5 This isn't an integer, thus complicating the search for integer solutions.
If we look at 3x + 6y = 24:
- We can simplify this to x + 2y = 8
- This gives us a family of solutions where x = 8 - 2y. Any integer value for y would produce an integer value for x.
For example:
- If y = 1, then x = 6
- If y = 2, then x = 4
- If y = 3, then x = 2
- and so on...
However, these solutions don't satisfy the first part of the original equation (5x + 5 = 24). This reinforces the idea that the original equation's presentation is misleading. We can't simply treat it as one equation but rather recognize it is (or should be) a system of equations, and a specific solution set will depend entirely on the method and whether we are seeking integer or non-integer solutions.
Conclusion: The Importance of Careful Analysis
The equation 5x + 5 = 3x + 6y = 24 highlights the importance of careful analysis in mathematical problem-solving. The seemingly simple structure hides a more complex reality involving systems of equations and different solution sets depending on the approach and the type of solutions sought (integer or non-integer). By breaking down the equation into its constituent parts, employing appropriate solution methods, and understanding the underlying mathematical concepts, we can successfully navigate the complexities and appreciate the broader applications of this type of problem. The equation serves as a valuable reminder that even seemingly simple mathematical problems can offer rich opportunities for learning and deeper exploration. Careful analysis is key to unlocking the secrets hidden within the numbers.
Latest Posts
Latest Posts
-
What Number Sentence Does This Model Show
Jun 08, 2025
-
Brake Fluid Expands And Contracts With Changes In Temperature
Jun 08, 2025
-
A Number Cube Numbered 1 6 Is Rolled Once
Jun 08, 2025
-
Which Sentence Is The Clearest Example Of Alliteration
Jun 08, 2025
-
What Is The Value Of The Underlined Digit 56
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about 5x Y 5 3x 6y 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.