6.012 As A Mixed Number In Simplest Form
Breaking News Today
Jun 07, 2025 · 5 min read
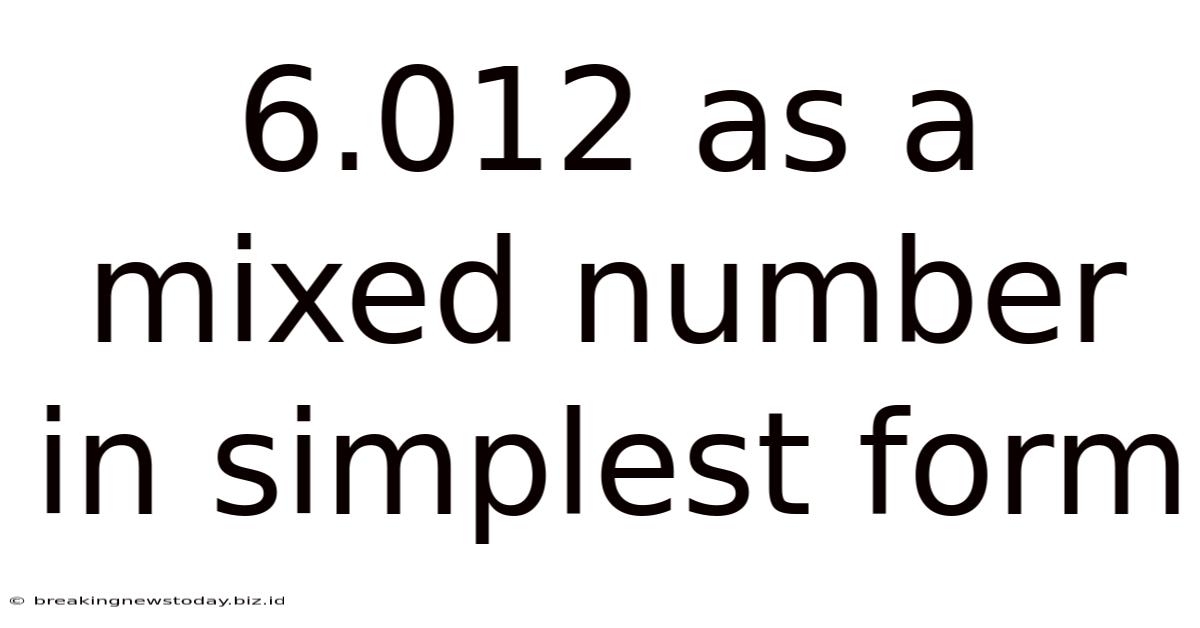
Table of Contents
6.012 as a Mixed Number in Simplest Form: A Comprehensive Guide
Converting decimals to fractions, and further simplifying them into mixed numbers, is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the decimal 6.012 into its simplest mixed number form, explaining each step in detail. We'll also explore the underlying concepts and provide additional examples to solidify your understanding.
Understanding Decimals and Mixed Numbers
Before we delve into the conversion, let's refresh our understanding of decimals and mixed numbers.
Decimals: A decimal is a number that uses a decimal point to separate the whole number part from the fractional part. The digits to the right of the decimal point represent fractions with denominators that are powers of 10 (10, 100, 1000, and so on). For example, in the decimal 6.012, the '6' represents the whole number part, while '.012' represents the fractional part, which is twelve thousandths (12/1000).
Mixed Numbers: A mixed number is a combination of a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). For example, 3 1/2 is a mixed number, where 3 is the whole number part and 1/2 is the proper fraction part. Mixed numbers are often used to represent quantities that are greater than one but not a whole number.
Converting 6.012 to a Fraction
The first step in converting 6.012 to a mixed number is to express it as an improper fraction (a fraction where the numerator is greater than or equal to the denominator). We can do this by considering the place value of each digit in the decimal:
- 6: Represents 6 whole units.
- 0: Represents 0 tenths (0/10).
- 1: Represents 1 hundredth (1/100).
- 2: Represents 2 thousandths (2/1000).
To combine these, we need a common denominator. The smallest common denominator for tenths, hundredths, and thousandths is 1000. Therefore, we can rewrite 6.012 as:
6 + 0/10 + 1/100 + 2/1000 = 6 + 0/1000 + 10/1000 + 2/1000 = 6 + 12/1000
This gives us the improper fraction 6 and 12/1000. However, we can represent the entire number as an improper fraction by multiplying the whole number (6) by the denominator (1000) and adding the numerator (12):
(6 * 1000) + 12 = 6012
So, 6.012 as an improper fraction is 6012/1000.
Simplifying the Fraction to its Simplest Form
The fraction 6012/1000 is not in its simplest form because both the numerator and the denominator can be divided by a common factor. To simplify, we need to find the greatest common divisor (GCD) of 6012 and 1000.
One method to find the GCD is to list the factors of both numbers and find the largest one they share. However, a more efficient method is using the Euclidean algorithm. This algorithm involves repeatedly dividing the larger number by the smaller number and taking the remainder until the remainder is 0. The last non-zero remainder is the GCD.
Let's apply the Euclidean algorithm:
- 6012 ÷ 1000 = 6 with a remainder of 12
- 1000 ÷ 12 = 83 with a remainder of 4
- 12 ÷ 4 = 3 with a remainder of 0
The last non-zero remainder is 4. Therefore, the GCD of 6012 and 1000 is 4.
Now, we can simplify the fraction by dividing both the numerator and the denominator by 4:
6012 ÷ 4 = 1503 1000 ÷ 4 = 250
This gives us the simplified fraction 1503/250.
Converting the Improper Fraction to a Mixed Number
Finally, we convert the simplified improper fraction 1503/250 into a mixed number. We do this by dividing the numerator (1503) by the denominator (250):
1503 ÷ 250 = 6 with a remainder of 3
The quotient (6) becomes the whole number part of the mixed number, and the remainder (3) becomes the numerator of the fractional part. The denominator remains the same (250).
Therefore, 6.012 as a mixed number in its simplest form is 6 3/250.
Further Examples and Practice
Let's try a few more examples to reinforce our understanding:
Example 1: Convert 2.75 to a mixed number in simplest form.
- Convert to an improper fraction: 2.75 = 275/100
- Find the GCD: The GCD of 275 and 100 is 25.
- Simplify the fraction: 275 ÷ 25 = 11; 100 ÷ 25 = 4. The simplified fraction is 11/4.
- Convert to a mixed number: 11 ÷ 4 = 2 with a remainder of 3. The mixed number is 2 3/4.
Example 2: Convert 0.625 to a mixed number in simplest form.
- Convert to an improper fraction: 0.625 = 625/1000
- Find the GCD: The GCD of 625 and 1000 is 125.
- Simplify the fraction: 625 ÷ 125 = 5; 1000 ÷ 125 = 8. The simplified fraction is 5/8.
- **Since the fraction is proper, the mixed number is simply 5/8.
Conclusion
Converting decimals to mixed numbers involves a series of steps: converting the decimal to an improper fraction, simplifying the fraction to its lowest terms by finding the greatest common divisor, and finally converting the simplified improper fraction to a mixed number. This process, while seemingly complex, becomes straightforward with practice. Remember to carefully follow each step, and you'll master this essential mathematical skill. Through consistent practice and a clear understanding of the underlying principles, you'll become proficient in converting decimals to their simplest mixed number equivalents. This skill is invaluable not only in mathematics but also in various real-world applications where precise calculations are required.
Latest Posts
Latest Posts
-
What Is The Only Cpr Performance Monitor Typically Available
Jun 07, 2025
-
Which Statement About Priorities Is Correct
Jun 07, 2025
-
Which Number Line Represents The Solution To 5x 30
Jun 07, 2025
-
Which Of The Following Best Describes Science Fiction
Jun 07, 2025
-
A Creditor Would Favor A Positive Net Worth
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 6.012 As A Mixed Number In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.