60 Twenty Fives Minus 1 Twenty Five
Breaking News Today
Jun 04, 2025 · 5 min read
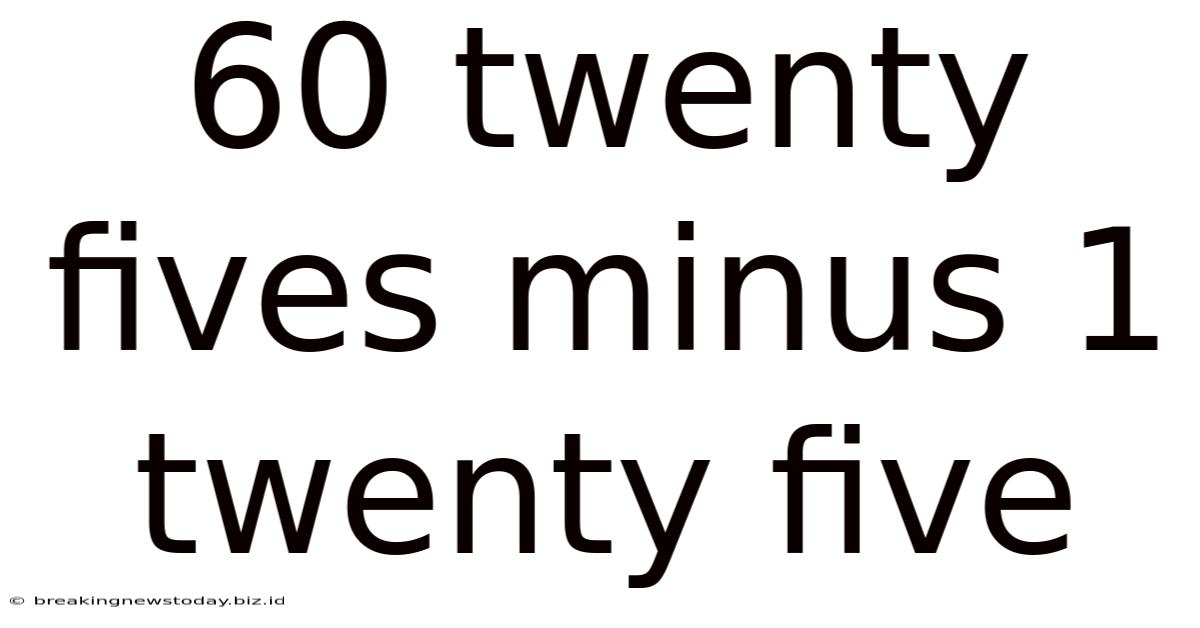
Table of Contents
60 Twenty-Fives Minus 1 Twenty-Five: A Deep Dive into Subtraction and its Applications
This seemingly simple arithmetic problem, "60 twenty-fives minus 1 twenty-five," offers a fascinating gateway to explore various mathematical concepts, their practical applications, and even their philosophical implications. While the immediate answer is straightforward, delving deeper reveals a rich tapestry of mathematical thinking and its relevance in our daily lives. This article will explore the problem, dissect its solution, and then broaden the discussion to encompass related mathematical concepts and real-world scenarios.
Understanding the Problem: A Foundation in Subtraction
At its core, "60 twenty-fives minus 1 twenty-five" is a subtraction problem. Subtraction is one of the four basic arithmetic operations, representing the removal of objects from a collection. In this case, we're dealing with a collection of "twenty-fives." This could represent anything from monetary units ($25) to groups of items (25 apples, 25 books, etc.). The problem essentially asks: if you have 60 units of 25, and you remove 1 unit of 25, how many units of 25 do you have left?
The Straightforward Solution
The most direct approach to solving this problem involves simple subtraction:
60 - 1 = 59
Therefore, 60 twenty-fives minus 1 twenty-five equals 59 twenty-fives.
This solution highlights the fundamental nature of subtraction as a process of reduction or decrease. It's a crucial operation used across numerous fields, from basic accounting to advanced scientific calculations.
Beyond the Basics: Exploring Related Mathematical Concepts
While the solution is simple, the problem provides an excellent springboard to explore more advanced mathematical concepts:
1. Multiplication and its Inverse Relationship with Division
We can reframe the problem using multiplication. "60 twenty-fives" can be expressed as 60 x 25. Similarly, "1 twenty-five" is 1 x 25. The problem then becomes:
(60 x 25) - (1 x 25) = ?
This highlights the distributive property of multiplication over subtraction:
(60 - 1) x 25 = 59 x 25 = 1475
This approach underscores the interconnectedness of arithmetic operations. Multiplication and division are inverse operations, meaning one undoes the other. The ability to seamlessly transition between multiplication and subtraction is vital for solving more complex problems.
2. The Concept of Sets and Set Theory
From a set theory perspective, we can view "twenty-fives" as elements within a set. The problem then involves manipulating sets: removing one element from a larger set. This concept is foundational in areas like computer science, statistics, and logic. Set theory provides a formal framework for reasoning about collections of objects and their relationships.
3. Abstract Algebra and Group Theory
While seemingly trivial, the problem touches upon abstract algebra concepts. The integers (whole numbers) form a group under addition, with subtraction being defined as the addition of the inverse. This abstract approach expands the understanding of operations beyond their concrete applications. Group theory finds extensive use in physics, cryptography, and computer science.
Real-World Applications: From Finances to Inventory
The seemingly simple "60 twenty-fives minus 1 twenty-five" problem finds numerous practical applications in everyday life:
1. Financial Calculations
Imagine a business dealing with inventory valued at $25 per unit. If they start with 60 units and sell one, the remaining inventory value is easily calculated using this subtraction problem. This simple calculation is fundamental to inventory management, profit calculation, and financial reporting.
2. Resource Management
This concept extends beyond monetary value. Consider a construction project using 25-kilogram bags of cement. If the project requires 60 bags and one bag is damaged, the remaining quantity is determined by the same subtraction. Resource management in various fields, from construction to agriculture, relies heavily on similar calculations.
3. Data Analysis and Statistics
In data analysis, subtracting one data point from a larger dataset might be necessary for various reasons, such as removing an outlier or correcting an error. The principle of subtracting a single element from a group of similar elements remains the same, regardless of the context.
4. Scientific Calculations and Measurement
In scientific research, subtracting measurements is commonplace. For instance, calculating the net change in a scientific experiment or removing background noise from a signal often involves subtracting values. The accuracy and precision of these calculations are critical to scientific validity.
Extending the Problem: Scaling Up and Adding Complexity
The basic problem can be easily scaled up. Consider "600 twenty-fives minus 10 twenty-fives" or even "6000 twenty-fives minus 100 twenty-fives". The fundamental principle remains the same, but the magnitude of the calculation increases. This highlights the scalability of mathematical operations and their ability to handle large datasets.
Adding complexity involves introducing more variables. For instance, consider a scenario where the value of "twenty-five" changes: "60 units of X minus 1 unit of X, where X = 25". This introduces algebraic thinking, allowing for the generalization of the problem and its application to a broader range of scenarios.
The Philosophical Implications: Subtraction as a Process of Change
Beyond the mathematical calculations, this problem touches upon the philosophical concept of change. Subtraction represents a reduction, a decrease, a transition from one state to another. This mirrors the constant change inherent in the universe. The act of removing one "twenty-five" signifies a modification, a transformation of the initial state. This concept has implications in various fields, from physics (decay processes) to philosophy (the nature of being and becoming).
Conclusion: A Simple Problem with Profound Implications
The seemingly simple problem, "60 twenty-fives minus 1 twenty-five," serves as a microcosm of mathematical thought. It demonstrates the interconnectedness of arithmetic operations, their applications in diverse fields, and their relevance to our understanding of the world. By dissecting this basic problem, we gain a deeper appreciation for the power and elegance of mathematics and its profound influence on our lives. The ability to solve this problem, and more importantly, to understand the underlying concepts, is a fundamental skill applicable across various disciplines and crucial for navigating the complexities of the modern world. From managing finances to understanding scientific data, the principles highlighted by this simple subtraction problem are essential for informed decision-making and effective problem-solving.
Latest Posts
Latest Posts
-
A Package Of Ground Beef Costs 6 98
Jun 06, 2025
-
Find The Sum Of 536 And 232
Jun 06, 2025
-
Express As A Single Natural Logarithm Ln 16 Ln 8
Jun 06, 2025
-
Which Of The Following Is True About Flemish Painting
Jun 06, 2025
-
Write The Chemical Formula For Dihydrogen Monotelluride
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about 60 Twenty Fives Minus 1 Twenty Five . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.