62 More Than A Number X Is Less Than 233.
Breaking News Today
Jun 07, 2025 · 6 min read
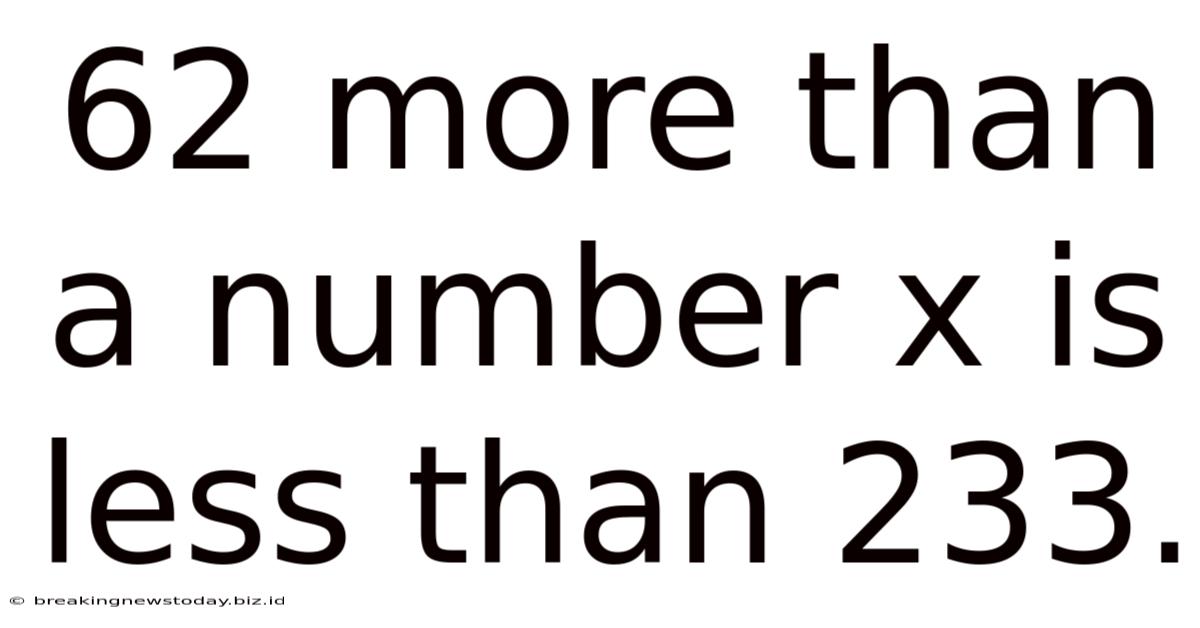
Table of Contents
62 More Than a Number x is Less Than 233: A Deep Dive into Inequalities
This seemingly simple statement, "62 more than a number x is less than 233," opens the door to a fascinating exploration of inequalities, their applications, and how to solve them. While the core concept might appear elementary, understanding its nuances is crucial for various mathematical applications, from basic algebra to advanced calculus and beyond. This article will delve into this inequality, demonstrating various approaches to solving it, exploring its graphical representation, and discussing its real-world applications.
Understanding the Inequality: Deconstructing the Problem
The phrase "62 more than a number x" translates mathematically to x + 62. The statement "is less than 233" translates to < 233. Therefore, the complete inequality is expressed as:
x + 62 < 233
This inequality signifies that the value of x + 62 lies on the number line somewhere to the left of 233; it is strictly less than 233. It does not include 233 itself. This is a key distinction that affects the solution set.
Solving the Inequality: Step-by-Step Approach
Solving this inequality involves isolating the variable x to determine its possible range of values. We achieve this using the properties of inequalities, similar to how we solve equations, but with a crucial difference: when multiplying or dividing by a negative number, the inequality sign flips.
Here's the step-by-step solution:
- Subtract 62 from both sides: This maintains the inequality's balance.
x + 62 - 62 < 233 - 62This simplifies to:x < 171
This result indicates that x can be any number strictly less than 171.
Representing the Solution Graphically: Visualizing the Inequality
Visualizing the solution set on a number line provides a clear understanding of the possible values of x.
-
Open Circle: Since the inequality is
x < 171, we use an open circle at 171 on the number line. The open circle signifies that 171 itself is not included in the solution set. -
Arrow to the Left: The arrow extends to the left from the open circle, indicating that all numbers less than 171 are part of the solution.
[Imagine a number line here with an open circle at 171 and an arrow pointing to the left. Unfortunately, I can't create images directly in this markdown format.]
Exploring the Solution Set: Infinite Possibilities
The solution x < 171 represents an infinite number of possibilities. x could be 170, 170.999, 0, -10, -1000, or any other number smaller than 171. This infinite nature is a characteristic of many inequalities.
Real-World Applications: Putting the Inequality to Work
While seemingly abstract, inequalities have numerous practical applications in various fields:
1. Budgeting and Finance:
Imagine you have a budget of $233 for groceries this week. You've already spent $62 on non-perishables. The amount you can spend on fresh produce (x) is represented by the inequality:
x + 62 ≤ 233 (Note: We use ≤ here because you can spend up to, and including, $233).
Solving this gives x ≤ 171, meaning you can spend a maximum of $171 on fresh produce.
2. Temperature Ranges:
A scientific experiment requires the temperature to remain below 233 degrees Kelvin. The current temperature is 62 degrees Kelvin higher than the target temperature (x). The inequality representing this scenario is:
x + 62 < 233
Solving this, we get x < 171 Kelvin. This tells the researchers the target temperature must be kept below 171 Kelvin.
3. Manufacturing Tolerances:
In manufacturing, precise measurements are crucial. Suppose a component needs to have a length less than 233 millimeters. Due to manufacturing imperfections, the actual length (x) could be 62 millimeters longer than the designed length. The inequality becomes:
x + 62 < 233
Solving yields x < 171 millimeters. This establishes the maximum acceptable length for the component.
4. Speed Limits:
Consider a scenario where a vehicle's speed must remain below 233 km/h. If the vehicle's current speed is 62 km/h faster than a safe speed (x), then the inequality is:
x + 62 < 233
Solving for x, we find that x < 171 km/h. This indicates the safe speed limit for that specific condition.
5. Resource Allocation:
A company has a total of 233 units of a particular resource. 62 units are already allocated to project A. The number of units that can be allocated to project B (x) is given by:
x + 62 ≤ 233
Solving, we get x ≤ 171, signifying that a maximum of 171 units can be allocated to Project B.
Compound Inequalities: Expanding the Possibilities
While the original problem focuses on a single inequality, the concept can extend to compound inequalities, involving multiple conditions. For instance, imagine a situation where 62 more than a number x is both less than 233 and greater than 100. This would be represented as:
100 < x + 62 < 233
To solve this, we subtract 62 from all three parts of the inequality:
100 - 62 < x < 233 - 62
38 < x < 171
This means x must fall between 38 and 171 (exclusive). The solution set now has a lower and upper bound.
Applications of Compound Inequalities
Compound inequalities are even more powerful in real-world situations. They allow for the modeling of situations with both upper and lower limits.
-
Weight Restrictions: A shipping container can carry a maximum weight of 233 kg. If the container already holds 62 kg, the additional weight (
x) that can be added is determined by 62 < x + 62 < 233. This constraint ensures the container isn’t overloaded while ensuring a minimum weight is maintained. -
Temperature Control: A process requires the temperature to stay within a specific range, say between 100 and 233 degrees Celsius. If the current temperature is 62 degrees Celsius higher than the target temperature (
x), then 100 < x + 62 < 233 will find the acceptable range for x. -
Performance Metrics: A product should maintain a quality score (x) above a certain minimum threshold, for example 38 points, whilst not exceeding a maximum score of 171 points, reflecting limitations in testing procedures.
Conclusion: Mastering Inequalities for Real-World Success
The seemingly simple inequality, "62 more than a number x is less than 233," provides a gateway to understanding the power and versatility of inequalities. Through step-by-step solving, graphical representation, and real-world applications, we've demonstrated the importance of this fundamental concept. From budgeting and finance to manufacturing and scientific research, inequalities play a vital role in modeling and solving various problems. Mastering the art of solving and interpreting inequalities is an essential skill for success in numerous fields. Understanding both simple and compound inequalities empowers you to tackle complex problems and make informed decisions based on quantitative data. This foundational knowledge opens up pathways to more advanced mathematical concepts and their applications in the real world.
Latest Posts
Latest Posts
-
Which Scenario Describes An Effect Of Tornadoes On The Environment
Jun 07, 2025
-
Mary And Lewis Each Open A Savings Account
Jun 07, 2025
-
The Two Basic Types Of Written Reports
Jun 07, 2025
-
Which Statement Best Describes The Progressives View On Conservation
Jun 07, 2025
-
Match Each Theory Of Emotion With Its Description
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 62 More Than A Number X Is Less Than 233. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.