6n 2 6n 5 7n 2 6n 5
Breaking News Today
Jun 01, 2025 · 5 min read
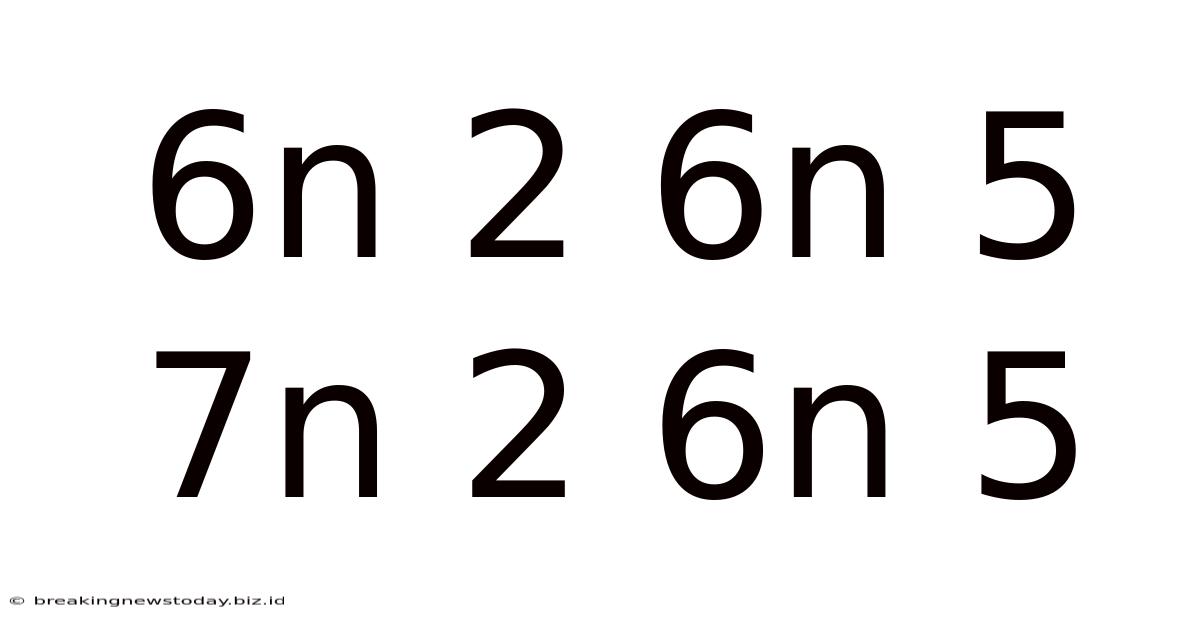
Table of Contents
Decoding the Enigma: A Deep Dive into 6n² + 6n + 5 and 7n² + 6n + 5
The seemingly simple expressions 6n² + 6n + 5 and 7n² + 6n + 5 might appear innocuous at first glance. However, a closer examination reveals a fascinating world of mathematical exploration, encompassing number theory, quadratic equations, and the surprising behavior of these seemingly straightforward quadratic functions. This article delves deep into the properties, patterns, and potential applications of these expressions, unveiling their hidden complexities and highlighting their significance within the broader landscape of mathematics.
Understanding the Basics: Quadratic Expressions
Before embarking on a detailed analysis of our chosen expressions, let's establish a foundational understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, 'n') is two. They generally take the form: an² + bn + c, where 'a', 'b', and 'c' are constants, and 'a' is non-zero. Our expressions, 6n² + 6n + 5 and 7n² + 6n + 5, conform perfectly to this structure.
The values of 'a', 'b', and 'c' significantly influence the characteristics of the quadratic function, determining its shape (a parabola), its vertex, and its intercepts. Analyzing these constants will be crucial to understanding the behavior of our expressions.
Analyzing 6n² + 6n + 5
Let's begin by scrutinizing the expression 6n² + 6n + 5. Notice that:
- a = 6: This positive value indicates that the parabola opens upwards, meaning the quadratic function has a minimum value.
- b = 6: This coefficient contributes to the position of the vertex and the axis of symmetry.
- c = 5: This is the y-intercept, representing the value of the function when n = 0.
This expression doesn't readily factor into simpler terms using integers. To find its roots (the values of 'n' for which the expression equals zero), we would need to employ the quadratic formula: n = [-b ± √(b² - 4ac)] / 2a. This reveals that the roots are complex numbers, implying that the parabola does not intersect the x-axis.
Analyzing 7n² + 6n + 5
The expression 7n² + 6n + 5 shares similarities with its counterpart, yet also exhibits distinct characteristics:
- a = 7: Like the previous expression, the parabola opens upwards due to the positive 'a' value.
- b = 6: The same 'b' coefficient suggests a similar influence on the vertex and axis of symmetry. However, the different 'a' value will shift the parabola.
- c = 5: The y-intercept remains the same, indicating the function takes the same value when n = 0.
Similar to 6n² + 6n + 5, this expression also does not factor neatly into simpler terms using integers. Applying the quadratic formula will again yield complex roots, confirming that the parabola does not intersect the x-axis.
Exploring Patterns and Sequences
While finding the roots offers valuable insight, investigating the sequences generated by these expressions for different integer values of 'n' unveils intriguing patterns. Let's consider the first few terms for both expressions:
6n² + 6n + 5:
- n = 0: 5
- n = 1: 17
- n = 2: 35
- n = 3: 61
- n = 4: 95
- n = 5: 137
7n² + 6n + 5:
- n = 0: 5
- n = 1: 18
- n = 2: 43
- n = 3: 76
- n = 4: 121
- n = 5: 175
Notice that both sequences increase rapidly, but at different rates. The differences between consecutive terms in each sequence also form their own sequences, highlighting the quadratic nature of the original expressions. Examining these difference sequences can further reveal underlying patterns. This methodology is a fundamental tool in number theory, often used to uncover hidden relationships between seemingly unrelated numbers.
Applications and Further Exploration
While these expressions might seem abstract, they have potential applications in various fields. Quadratic equations form the bedrock of many physics problems involving projectile motion, for example. Understanding the behavior of these specific quadratic expressions can contribute to solving such problems within specific contexts. Furthermore, the exploration of sequences generated by these expressions can offer insights into number theory and pattern recognition. This analysis can be extended by considering:
- Modulo Arithmetic: Investigating the remainders when these expressions are divided by various integers can reveal cyclical patterns or other interesting properties.
- Prime Numbers: Analyzing the values generated by the expressions to determine if they frequently produce prime numbers or have a relationship to prime number distribution could offer a fascinating area of research.
- Continued Fractions: Representing the roots of these quadratic equations using continued fractions might expose hidden symmetries or relationships.
- Computer Programming: Implementing algorithms to generate and analyze these sequences using programming languages can facilitate large-scale investigations and visualization.
Conclusion: The Beauty of Mathematical Exploration
The seemingly simple expressions 6n² + 6n + 5 and 7n² + 6n + 5 offer a compelling case study in the power of mathematical exploration. Through a careful analysis of their properties, the sequences they generate, and the various mathematical tools that can be applied, we uncover a depth and complexity far exceeding their initial appearance. This journey highlights the interconnectedness of different mathematical fields and encourages further investigation into the hidden patterns and relationships that lie beneath the surface of even the simplest mathematical expressions. The continued exploration of these and similar expressions can lead to new discoveries and deepen our understanding of the fundamental principles governing the world of numbers. The seemingly simple can often hold the key to surprising and profound mathematical beauty. The journey of discovery, as demonstrated here, is an endlessly rewarding one, revealing the hidden richness within even the most basic mathematical forms. Further research into these expressions, using the diverse methodologies outlined above, promises to unearth even more fascinating properties and patterns, solidifying the importance of continued mathematical inquiry and investigation.
Latest Posts
Latest Posts
-
The Ions In Most Ionic Compounds Are Organized Into A
Jun 02, 2025
-
Why Might Raising Taxes Be A Risk For Struggling Cities
Jun 02, 2025
-
How Many Morphemes Are There In The Word Bats
Jun 02, 2025
-
A Northern Renaissance Writer Who Criticized The Catholic Church Was
Jun 02, 2025
-
Which Of The Following Statements Regarding Merchandise Inventory Is False
Jun 02, 2025
Related Post
Thank you for visiting our website which covers about 6n 2 6n 5 7n 2 6n 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.