7.02 Is 10.4 Of What Number
Breaking News Today
Jun 07, 2025 · 5 min read
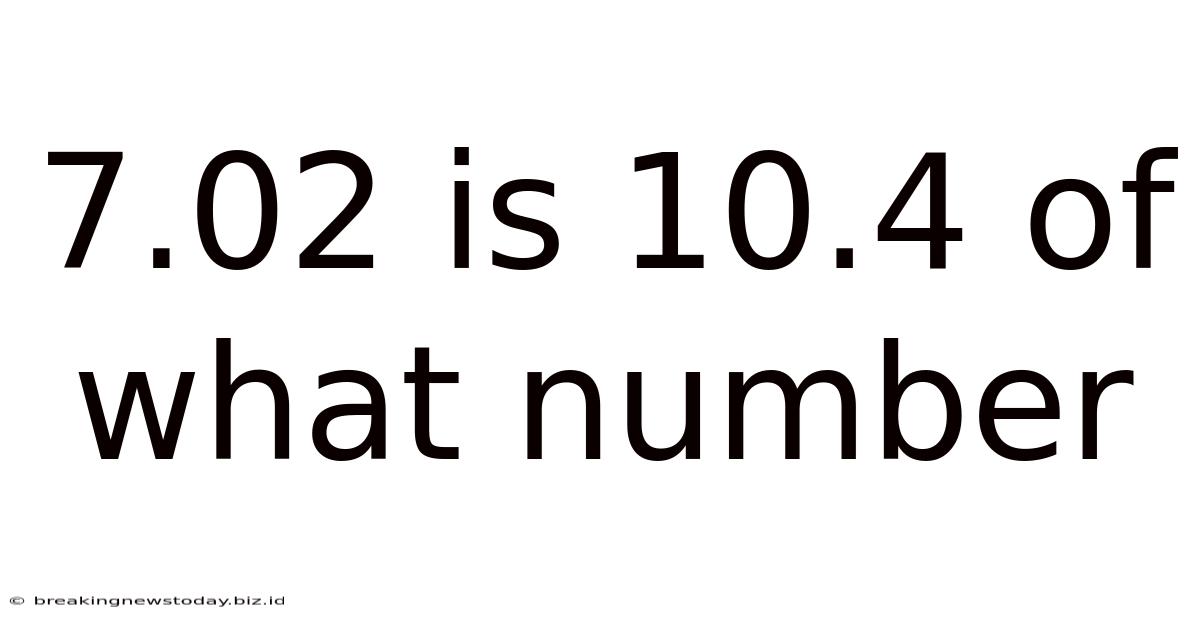
Table of Contents
7.02 is 10.4% of What Number? A Comprehensive Guide to Solving Percentage Problems
Percentage problems are a common part of everyday life, from calculating discounts and taxes to understanding statistics and financial reports. This article will delve deep into solving the specific problem: "7.02 is 10.4% of what number?" We'll explore multiple methods, explain the underlying concepts, and provide practical examples to enhance your understanding of percentages and their applications.
Understanding Percentages
Before we dive into the solution, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. For instance, 10% means 10 out of 100, which can also be written as 10/100 or 0.10 as a decimal.
Understanding this fundamental concept is crucial for solving percentage problems. We often use percentages to represent proportions or parts of a whole. In our problem, "7.02 is 10.4% of what number?", we are essentially trying to find the "whole" number of which 7.02 represents 10.4%.
Method 1: Using the Formula
The most straightforward way to solve percentage problems is by using the basic percentage formula:
Part = Percentage × Whole
In our problem:
- Part = 7.02
- Percentage = 10.4% = 0.104 (Remember to convert the percentage to a decimal by dividing by 100)
- Whole = This is what we need to find (let's represent it with 'x')
Substituting these values into the formula, we get:
7.02 = 0.104 × x
To solve for 'x', we need to isolate it by dividing both sides of the equation by 0.104:
x = 7.02 / 0.104
Calculating this gives us:
x ≈ 67.5
Therefore, 7.02 is approximately 10.4% of 67.5.
Method 2: Using Proportions
Another effective method for solving percentage problems is using proportions. A proportion is an equation that states two ratios are equal. We can set up a proportion based on our problem:
7.02 / x = 10.4 / 100
This proportion states that the ratio of the part (7.02) to the whole (x) is equal to the ratio of the percentage (10.4) to 100.
To solve this proportion, we can cross-multiply:
7.02 × 100 = 10.4 × x
702 = 10.4x
Now, we isolate 'x' by dividing both sides by 10.4:
x = 702 / 10.4
x ≈ 67.5
Again, we arrive at the solution: 7.02 is approximately 10.4% of 67.5.
Method 3: Working Backwards from the Percentage
This method involves understanding the relationship between the percentage and the whole. If 7.02 represents 10.4%, we can find the value of 1% by dividing 7.02 by 10.4:
1% = 7.02 / 10.4 ≈ 0.675
Since 1% represents 0.675, we can find the whole (100%) by multiplying 0.675 by 100:
100% = 0.675 × 100 = 67.5
This confirms our previous results: 7.02 is approximately 10.4% of 67.5.
Practical Applications and Real-World Examples
Understanding how to solve percentage problems like this one has numerous practical applications in various aspects of life:
1. Finance and Budgeting:
- Calculating interest: If you earn 10.4% interest on an investment and receive $7.02 in interest, you can use this method to determine the principal amount of your investment.
- Analyzing financial statements: Percentage calculations are essential for interpreting financial ratios and understanding profit margins, growth rates, and other key performance indicators.
- Determining discounts: If an item is discounted by 10.4% and the discount amount is $7.02, you can find the original price.
2. Sales and Marketing:
- Tracking conversion rates: Businesses use percentages to track the effectiveness of marketing campaigns by calculating the percentage of leads that convert into sales.
- Analyzing market share: Companies use percentages to determine their share of a particular market.
- Calculating commission: Salespeople often earn a commission based on a percentage of their sales.
3. Education and Statistics:
- Calculating grades: Grades are often expressed as percentages reflecting performance on exams or assignments.
- Interpreting statistical data: Percentages are widely used to represent proportions and probabilities in various statistical analyses.
- Understanding survey results: Survey results often present data as percentages, allowing for easy comparison and interpretation.
4. Everyday Life:
- Calculating tips: Determining a tip amount in a restaurant often involves calculating a percentage of the bill.
- Understanding tax rates: Sales tax and income tax are expressed as percentages of the purchase or income amount.
- Comparing prices: When shopping, comparing prices and discounts often requires working with percentages.
Troubleshooting and Common Mistakes
While solving percentage problems is relatively straightforward, some common mistakes can lead to incorrect results:
- Incorrect decimal conversion: Failing to convert the percentage to a decimal (by dividing by 100) is a common error. Always remember to convert the percentage to a decimal before using it in calculations.
- Incorrect order of operations: When using the formula, ensure you follow the correct order of operations (multiplication before division).
- Rounding errors: Be mindful of rounding errors, especially when dealing with multiple calculations. Try to avoid rounding until the final step to minimize inaccuracies.
- Using the wrong formula: Make sure you're using the correct formula for the specific type of percentage problem you're trying to solve.
Conclusion
Solving percentage problems, like determining that 7.02 is approximately 10.4% of 67.5, is a valuable skill applicable across various fields. By understanding the underlying principles and utilizing the different methods outlined in this article, you can confidently tackle similar problems and effectively interpret percentage-based data in your daily life and professional endeavors. Remember to practice regularly and pay attention to detail to avoid common mistakes and ensure accurate calculations. Mastering percentage calculations will empower you to analyze data more effectively, make informed decisions, and enhance your overall problem-solving skills.
Latest Posts
Latest Posts
-
Which Underlined Phrases Are Gerund Phrases Select Two Options
Jun 08, 2025
-
What Was Howard Gardners Concern About Traditional Intelligence Tests
Jun 08, 2025
-
A Fire Hydrant Sits 72 Feet
Jun 08, 2025
-
Which Sentences Show Correct Dialogue Punctuation Select Three Options
Jun 08, 2025
-
Which Of The Following Were The First Surfactants
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about 7.02 Is 10.4 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.