7 9 Divided By 2 3
Breaking News Today
Jun 08, 2025 · 5 min read
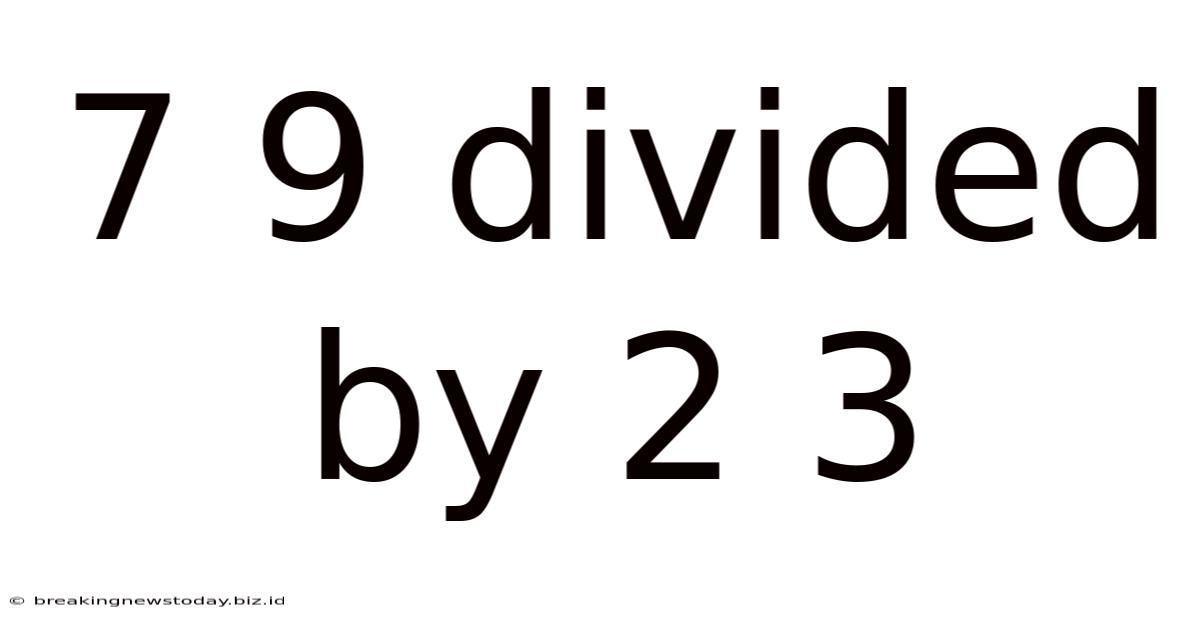
Table of Contents
79 Divided by 23: A Deep Dive into Division and its Applications
This article will explore the seemingly simple mathematical operation of dividing 79 by 23, delving far beyond the basic answer. We'll examine the process, discuss different methods of calculation, and explore the broader implications of division within mathematics and its real-world applications. Our focus will be on providing a comprehensive understanding, suitable for a wide range of readers, from those brushing up on their basic arithmetic to those interested in the underlying principles of mathematics.
Understanding the Problem: 79 ÷ 23
At its core, the problem 79 ÷ 23 asks: "How many times does 23 fit into 79?" This seemingly straightforward question opens the door to a fascinating exploration of mathematical concepts. The answer isn't a whole number; the division results in a quotient and a remainder. Let's delve into the methods of solving this.
Method 1: Long Division
Long division is a classic method taught in schools. It's a systematic approach that allows us to break down the division into manageable steps:
-
Set up the problem: Write 79 inside the long division symbol (⟌) and 23 outside.
-
Determine the quotient: Ask yourself, "How many times does 23 go into 79?" A quick estimate shows it's approximately 3 times (23 x 3 = 69).
-
Multiply and subtract: Multiply the divisor (23) by the quotient (3) to get 69. Subtract this from the dividend (79): 79 - 69 = 10.
-
The remainder: The result (10) is the remainder. This signifies that 23 fits into 79 three times with 10 left over.
Therefore, 79 ÷ 23 = 3 with a remainder of 10. We can also express this as a mixed number: 3 10/23.
Method 2: Using a Calculator
Modern technology simplifies calculations. A simple calculator can provide the answer instantly. Inputting 79 ÷ 23 will yield a decimal result, which will likely be 3.43478 (approximately). This decimal representation shows the remainder incorporated into the answer. While convenient, it's crucial to understand the underlying process of long division to fully grasp the concept.
Method 3: Estimation and Approximation
Before reaching for a calculator, estimating the answer can be valuable. We know 23 is close to 25, and 79 is close to 75. Dividing 75 by 25 gives 3. This quick estimate provides a reasonable approximation of the actual answer. Approximation skills are critical in many real-world applications where precise calculations may not always be necessary.
Beyond the Basic Calculation: Exploring Deeper Concepts
While finding the answer to 79 ÷ 23 is relatively simple, the process touches upon fundamental mathematical principles:
1. Divisibility Rules:
Understanding divisibility rules can help in quickly checking whether a number is divisible by another. While there's no simple divisibility rule for 23, understanding these rules for other numbers aids in estimation and simplification. For instance, knowing that a number is divisible by 2 if it's even, or divisible by 3 if the sum of its digits is divisible by 3, helps in simplifying larger division problems.
2. Prime and Composite Numbers:
The numbers involved in our calculation, 79 and 23, offer a glimpse into prime and composite numbers. 23 is a prime number (only divisible by 1 and itself), while 79 is also a prime number. Understanding prime factorization allows for a more profound understanding of number theory and its applications in cryptography and other fields.
3. Fractions and Decimals:
Expressing the remainder as a fraction (10/23) or a decimal (approximately 0.43478) demonstrates the relationship between fractions and decimals. This understanding is crucial for various mathematical applications, from geometry to calculus.
4. Real-World Applications:
The division operation is fundamental in numerous real-world scenarios:
-
Sharing: Dividing 79 candies among 23 children demonstrates a practical application of division. Each child gets 3 candies, and 10 candies remain.
-
Measurement: If you have a 79-inch piece of wood and need to cut it into 23-inch pieces, the division shows you can make 3 pieces, and you'll have a 10-inch piece left.
-
Resource Allocation: Dividing resources (budget, time, materials) among multiple projects frequently involves this type of calculation.
-
Averaging: Calculating averages often involves division.
Expanding the Scope: Advanced Mathematical Concepts
The simple problem of 79 ÷ 23 can serve as a springboard to explore more complex mathematical concepts:
1. Modular Arithmetic:
The remainder (10) in our calculation is central to modular arithmetic. This branch of number theory deals with remainders after division. In modular arithmetic (modulo 23), 79 is congruent to 10 (written as 79 ≡ 10 (mod 23)). Modular arithmetic is fundamental in cryptography, computer science, and other fields.
2. Continued Fractions:
The decimal representation of 79/23 can be expressed as a continued fraction. This is an alternative way to represent a number as a sum of fractions. Continued fractions have applications in number theory and approximation theory.
3. Number Theory:
The properties of the numbers 79 and 23, being prime numbers, connect to various theorems and concepts within number theory, a branch of mathematics dealing with the properties of integers.
Conclusion: The Significance of a Simple Division Problem
While seemingly elementary, the division of 79 by 23 offers a window into the vast and interconnected world of mathematics. From basic arithmetic operations to advanced concepts in number theory and their real-world applications, this simple problem showcases the power and beauty of mathematical principles. Understanding the different methods of solving this problem, combined with the exploration of related concepts, provides a strong foundation for further mathematical exploration and problem-solving. The seemingly simple act of division reveals a wealth of mathematical depth and practical applicability, emphasizing the importance of understanding mathematical foundations and their relevance in various fields. Whether you're a student reinforcing fundamental skills or an enthusiast exploring the intricacies of mathematics, this analysis serves as a testament to the enduring relevance of basic arithmetic and its far-reaching implications.
Latest Posts
Latest Posts
-
The Purpose Of These Lines Is To
Jun 08, 2025
-
What Is The Measure Of Fsm
Jun 08, 2025
-
Which Of The Following Diagrams Involves A Virtual Image
Jun 08, 2025
-
Focus On Managing Documents Communicating And Scheduling
Jun 08, 2025
-
An Insurer Devises An Intimidation Strategy
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about 7 9 Divided By 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.