7 Is Ten Times The Value Of
Breaking News Today
Jun 06, 2025 · 7 min read
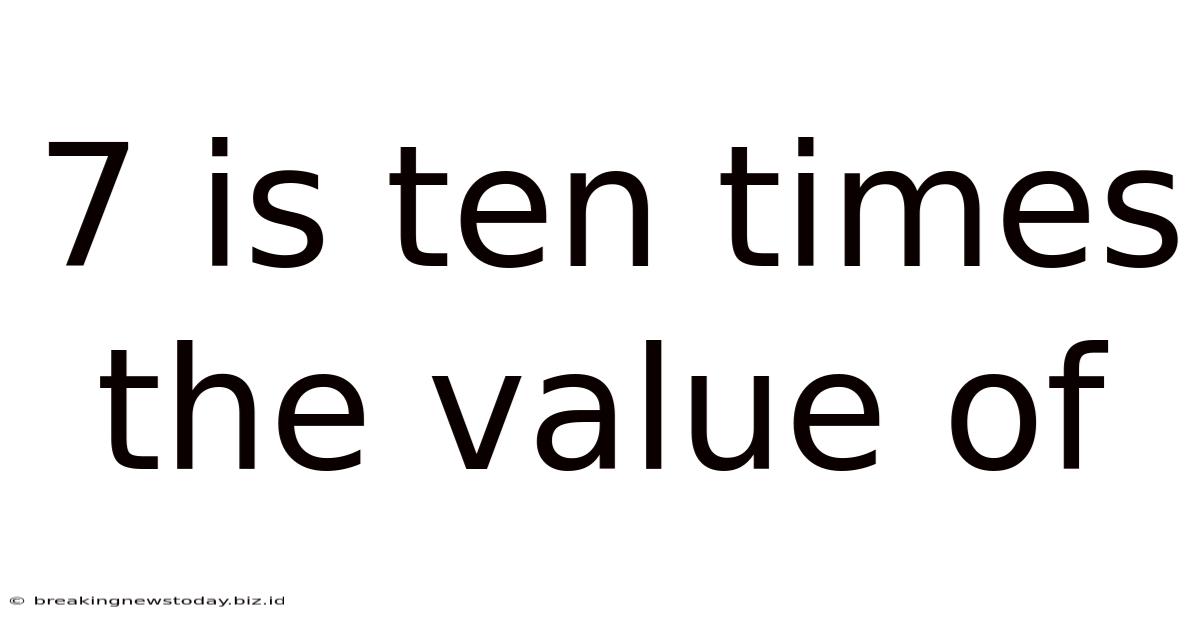
Table of Contents
7 is Ten Times the Value of: Exploring Place Value and Decimal Representation
Understanding the relationship between numbers, particularly how place value affects their magnitude, is fundamental to mathematical literacy. The statement "7 is ten times the value of" is incomplete, but it sets the stage for a crucial exploration of place value and how it dictates the numerical significance of digits within a number. This article will delve into this concept, examining various representations of numbers, including decimals and exploring its implications in real-world applications.
Understanding Place Value: The Foundation of Numerical Significance
The concept of place value is the cornerstone of our number system. It dictates that the value of a digit depends on its position within a number. Consider the number 70. The digit 7 isn't simply 7; it represents 7 tens, or 70. In contrast, the digit 7 in the number 7 represents seven ones. This seemingly simple difference highlights the profound impact of place value on the magnitude of a number.
The place values in our decimal system are based on powers of ten. Moving from right to left, we have:
- Ones (10<sup>0</sup>): The rightmost digit represents the number of ones.
- Tens (10<sup>1</sup>): The next digit to the left represents the number of tens.
- Hundreds (10<sup>2</sup>): The next digit represents the number of hundreds, and so on.
This pattern continues indefinitely for whole numbers, extending to thousands, millions, billions, and beyond. Each position represents a tenfold increase in value compared to the position to its right. This is the key to understanding the statement "7 is ten times the value of..." The missing part of the sentence would be "0.7" or "7/10".
Completing the Sentence: 7 is Ten Times the Value of 0.7
Let's complete the sentence: 7 is ten times the value of 0.7. This illustrates the relationship between whole numbers and decimals. 0.7 represents seven-tenths (7/10). Multiplying 0.7 by 10 shifts the decimal point one place to the right, resulting in 7. This directly demonstrates the tenfold increase in value due to the change in place value.
Exploring Decimal Representation: Expanding the Concept
The decimal system, based on powers of ten, allows us to represent numbers that are less than one. The digits to the right of the decimal point represent fractions of one. Each position to the right represents a tenth, a hundredth, a thousandth, and so on, decreasing in value by a factor of ten with each successive position.
- Tenths (10<sup>-1</sup>): The first digit to the right of the decimal point represents tenths.
- Hundredths (10<sup>-2</sup>): The second digit represents hundredths.
- Thousandths (10<sup>-3</sup>): The third digit represents thousandths, and so on.
Consider the number 7.77. This number contains:
- Seven ones: 7 x 10<sup>0</sup> = 7
- Seven tenths: 7 x 10<sup>-1</sup> = 0.7
- Seven hundredths: 7 x 10<sup>-2</sup> = 0.07
The total value is the sum of these components: 7 + 0.7 + 0.07 = 7.77. Each digit contributes to the overall value based on its position relative to the decimal point.
Real-World Applications of Place Value: Beyond the Classroom
The understanding of place value is far from an abstract mathematical concept; it has significant real-world implications. Its applications are pervasive, influencing various aspects of our daily lives:
1. Finance and Accounting: Accurate financial calculations depend entirely on understanding place value. A misplaced decimal point in a financial transaction, for instance, could lead to significant errors, costing individuals or businesses substantial amounts of money. From balancing checkbooks to managing large-scale investments, precise understanding of place value is paramount.
2. Measurement and Engineering: In engineering and scientific fields, precise measurements are critical. Understanding place value ensures accuracy in calculations related to length, weight, volume, and other physical quantities. A misinterpretation of place value in engineering could lead to structural failures or malfunctions of machinery, with potentially catastrophic consequences.
3. Data Analysis and Statistics: The interpretation of data sets relies heavily on understanding place value. When dealing with large datasets, the ability to interpret and analyze numbers with varying magnitudes is crucial. Incorrect understanding of place values can lead to misinterpretations and flawed conclusions in statistical analyses.
4. Everyday Transactions: Even everyday purchases involve an implicit understanding of place value. When we pay for groceries or calculate the tip at a restaurant, we are working with decimal representations of monetary values, relying on our understanding of place value to ensure accurate transactions.
Expanding the Concept: Different Number Systems
While the decimal system (base 10) is the most commonly used, other number systems exist. These systems use different bases, meaning they utilize a different number of digits to represent values. For example, the binary system (base 2) uses only two digits (0 and 1) and is fundamental to computer science.
Understanding place value is crucial regardless of the number system employed. The principles remain the same, although the magnitude of each position changes according to the base of the system. For example, in a binary system, the place values would be powers of 2 instead of powers of 10.
Challenges and Misconceptions in Understanding Place Value
Despite its seeming simplicity, several challenges and misconceptions can arise when dealing with place value, especially when working with decimals:
1. Misplacement of the Decimal Point: One of the most common errors involves misplacing the decimal point, leading to significant inaccuracies in calculations. This issue is particularly prevalent when dealing with numbers with many decimal places or when performing calculations involving large numbers and decimals simultaneously.
2. Confusion with Decimal Places: Students may struggle to comprehend the decreasing values of digits as you move further to the right of the decimal point. The subtle differences between tenths, hundredths, and thousandths, can be difficult to grasp.
3. Difficulty in Converting Between Fractions and Decimals: Converting fractions to decimals and vice versa can present difficulties for some learners. Understanding the relationship between the denominator of a fraction and the place value in the decimal representation is key to accurate conversion.
Strategies for Improving Understanding of Place Value
To overcome these challenges and improve understanding, several strategies are helpful:
1. Hands-on Activities: Using manipulatives like base-ten blocks can provide a concrete understanding of place value. Students can physically represent numbers and manipulate the blocks to visualize the relationships between different place values.
2. Real-world Examples: Connecting place value concepts to real-world situations, like money or measurement, can make the concept more relatable and easier to understand. Students can be encouraged to apply their knowledge of place value to solve problems involving everyday transactions or calculations.
3. Practice and Repetition: Regular practice with various exercises, such as comparing numbers, ordering numbers, and performing calculations involving decimals, can reinforce the understanding of place value and improve proficiency.
4. Visual Aids: Using charts, diagrams, and other visual aids can help students visualize the different place values and the relationships between them. This visual representation can improve comprehension and retention.
5. Games and Interactive Activities: Employing engaging games and interactive activities can make learning more fun and effective. Games involving place value can help reinforce concepts and improve understanding in a stimulating and interactive environment.
In conclusion, the seemingly simple statement "7 is ten times the value of..." opens a door to a deeper understanding of place value, a fundamental concept underpinning our number system. Its implications reach far beyond the classroom, impacting various fields and everyday life. By grasping this concept thoroughly, we enhance our numerical literacy and equip ourselves with essential skills for navigating the quantitative aspects of our world. Through practical application, hands-on activities, and continuous practice, we can solidify our comprehension of place value and its crucial role in mathematics and beyond.
Latest Posts
Latest Posts
-
The Upper Half Of An Oblong Shape Is The
Jun 06, 2025
-
6 1 Reteach To Build Understanding Answer Key
Jun 06, 2025
-
What Is The Solubility Of Kcl At 5 C
Jun 06, 2025
-
Adolfo Dom Nguez Usa Telas Y En Su Ropa
Jun 06, 2025
-
What Was One Of The Primary Lessons Learned From Lovaas
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about 7 Is Ten Times The Value Of . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.